Однородные уравнения первого порядка
Однородное уравнение можно представить в виде: y'(x)=φ(y/x) (1)
, где φ - некоторая функция. Например: : y'(x)=2+y/x .
Для его решения вводим дополнительную неизвестную функцию u(x), связанную с у(х) соотношением у(х)=u(x)*х. Делается это потому, что уравнение для u(x) оказывается более простым (уравнением с разделяющимися переменными).
Для получения этого уравнения подставляем в (1) вместо у выражение u*x.
Получим:
(u(x)*x)'=φ((ux)/x) --> u'*x+u*x'= φ(u) --> u'*x= φ(u) — u*1 -->
u'/(φ(u) — u)=1/x (2)
ДУ (2) — уравнение с разделяющимися переменными (все u -слева, х - справа).
Находим u(x) и затем получаем формулу для y(x): у = u(x)*х.
Примеры
1) xy'=x+2y
Решение. Делим уравнение на х. ---> y'=1+2y/x ---> Представляем у в виде: y=u(x)x. Подставляем u*x вместо у в уравнение. ---> Получаем (ux)' = 1+2u ---> u'*x+u*x'=1+2u ---> u'*x+u*x'=1+2u --->
u'*x =1+u (т.к. х'=1) ---> u'/(1+u) =1/x (делим обе части уравнения на x*(1+u))
Получаем уравнение с разделяющимися переменными для u(x). Решаем его/
(1/(1+u))du=(1/x)dx ---> ∫1/(1+u)du=∫(1/x)dx ---> ln|1+u| = ln|x| +C = ln|x| +ln|C1 |= ln|xC1 | ---> ln|1+u| = ln|xC1| ---> Из равенства логарифмов следует равенство их аргументов:
|1+u| = |xC1| ---> 1+u = ±|C1| x = C2x ---> u(x)= C2x -1 .
Далее находим y(x)=u*x= (C2x -1)*x
Ответ: y(x) = (C2x -1)*x
2)


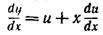

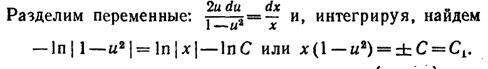
--> 1-u2=C1/x; u(x)=±√(1-C1/x);
Ответ: y(x)=xu=)=±x√(1-C1/x);
3)

( или x2-2y2+2xyy'=0 Делим на х2: 1-2(y/x)2 +2(y/x)y'=0 - однородн. уравн.)
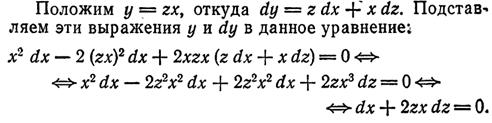

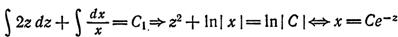
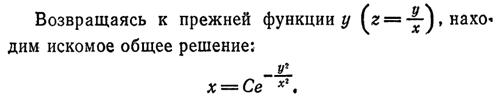
--> -y2/x2=ln(x/C) Ответ: y/x=±√(-ln(x/C)) = ±√(ln(C/x))
Упражнения.
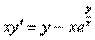 Ответ:
Ответ: 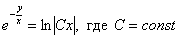
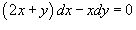 Ответ:
Ответ: 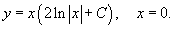
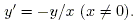 Ответ: ху=С и y=C/x
Ответ: ху=С и y=C/x
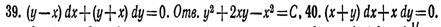
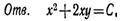
* * *
Линейные дифференциальные уравнения первого порядка
Линейным дифференциальным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и ее производной: y'(x) + P(x)y(x) = Q(x) (1)
Например: y'(x) + x*y(x) = 3 .
Решение:
- Мы ищем неизвестную функцию у(х), вводя две новые неизвестные функции u(x) и v(x), с помощью соотношения: y=u*v. (2)
- Мы требуем, чтобы v(x) удовлетворяло уравнению : v'(x) + P(x)v(x) =0 (3)
которое является уравнением с разделяющимися переменными.
Находим v(x), решая уравнение с разделяющимися переменными (3).
(Подчеркнем, что нам не нужно общее решение уравнения (3), а одно конкретное решение.
Например, вместо выражения v=2x+C далее используем v=2x, или вместо v=Cx - формулу v=x).
- Можно показать, что тогда функция u(x) удовлетворяет уравнению: u'*v=Q (4)
, которое также является уравнением с разделяющимися переменными
(действительно, если подставить y=u*v в уравнение (1), то, с учетом (3), получим: u'v=Q ) .
Представляем (4) в виде: u'=Q(x)/v(x) (5) ( где v(x) — найдено ранее).
 Находим u(x):
Находим u(x):
- Затем находим y(x): y=uv
Суммируем алгоритм решения:
1) Приводим заданное уравнение к виду y'(x) + P(x)y(x) = Q(x)
2) Составляем и решаем уравнение v'(x) + P(x)v(x) =0
3) Составляем уравнение u'v=Q и находим из него u(x)
4) Находим у(х) по формуле у=u*v
Примеры с решениями.
1) y'+3y=2;
1-й шаг. v'+3v=0; v'/v= - 3; ∫1/vdv = ∫-3dx; ln|v|=-3x+C;
v=±e-3x+C; v=± e-3xeC; v=C1e-3x , где C1 = ± eC ; v=e-3x
В выше приведенных выкладках почти до конца сохранена постоянная С и знак +-(с целью упражнения). Однако, следует подчеркнуть, что при нахождении v нам нужно только одно решение и , поэтому, в ln|v|=-3x+C следует сразу же положить С=0. Таким образом должно быть: ln|v|= - 3x; v=+- e-3x; v=e-3x
2-й шаг. u'v=2 --> u'e-3x=2 --> u '=2/e-3x --> u'=2e3x --> u= (2/3)e3x +C;
3-й шаг. y=u*v= ((2/3)e3x +C)* e-3x = 2/3e3xe-3x+ C* e-3x --> y= 2/3+ C* e-3x
2) 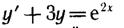

v' +3v = 0 --> dv/v = -3dx --> ln|v| = - 3x + ln|C1| --> v = ∫C1e-3x = C e-3x
u' =Q/v = e2x / e-3x = e5x --> u=1/5*e5x + C y=uv -->
Ответ: 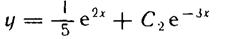
3)
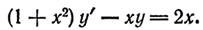
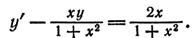
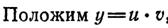



(Т.е. u — решение однородного уравнения с 0 в правой части , выше оно обозначалось через v).
Тогда:
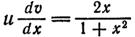
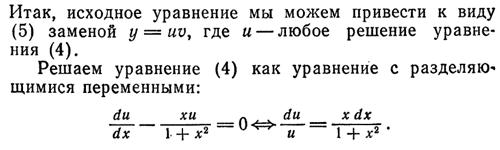
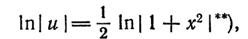
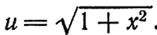

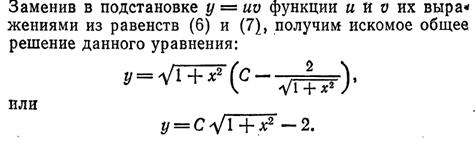
4)
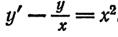
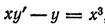
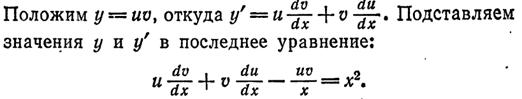 --->
--->
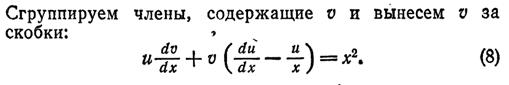
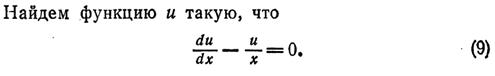
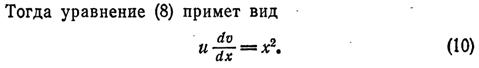

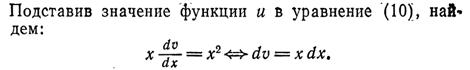
 Следовательно:
Следовательно:
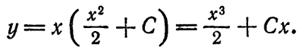
5) 
y' - 2/(2x+1) = 4x/(2x+1) - это линейное уравнение 1-го порядка
Сначала решим однородное уравнение с правой частью, равной нулю.
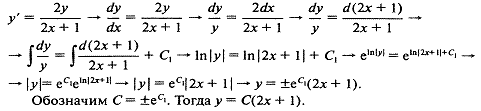
Выбираем решение с С=1: y=2x+1 .
Тогда v'=4x/(2x+1)2
v(x)=
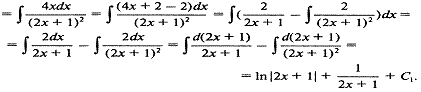
Окончательно: y(x) = 
Упражнения.
3) 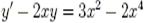 Ответ: у= х3+Cexp(x2)
Ответ: у= х3+Cexp(x2)
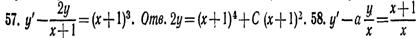
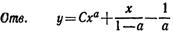
* * *
Линейные однородные уравнения второго порядка с постоянными коэффициентами
y''(x) + p*y'(x) + q*y(x) =0 (1)
где p,q - числа. Например: y''(x) + 3*y'(x) + 2*y(x) =0
Уравнение называется однородным, если в правой части уравнения - ноль, и неоднородным, если в правой части - функция f(x),отличная от 0.
Уравнение (1) имеет два линейно независимых решения : y1(x) и y2(x).
(Функции y1(x) и y2(x), неравные нулю тождественно, называются линейно независимыми, если C1*y1(x)+C2*y2(x) ≡0 тождественно равно нулю тогда и только тогда, когда С1=С2=0).
Общее решение (1) имеет вид: y(x) = C1*y1(x)+C2*y2(x).
Решение. Будем искать решение в виде: y=ekx, где k - неизвестная постоянная. Подставив y=ekx в (1), получим: ekx(k2+pk+q)=0. Отсюда:
k2+pk+q=0 - квадратное уравнение для определения k
(оно называется характеристическим для уравнения (1)).
Корни этого алгебраического уравнения можно найти по формулам:
k1= -p/2 + √(p2/4-q) ; k2= -p/2 - √(p2/4-q) (2)
Эти формулы дают значения корней уравнения (1), в котором множитель при k2 равен 1.
В общем случае уравнения ak2+bk+c=0 имеем D= b2-4ac и:
k1= [-b + √(b2-4ac)]/(2a) ; k2=[-b - √(b2-4ac)]/(2a) (3)
Линейно независимые решения ДУ y1(x) и y2(x) строятся описанным ниже образом..
Дата добавления: 2018-06-01; просмотров: 323; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
