Примеры решения задач в цепи второго порядка.
Задача 1. Переходный процесс в цепи второго порядка с постоянным источником питания и действительными различными корнями характеристического уравнения.
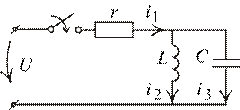 Рис. 1.65
Рис. 1.65
|
Условие:
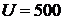 (В);
(В); 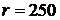 (Ом);
(Ом);
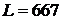 (мГн);
(мГн);  (мкФ).
(мкФ).
Определить мгновенные значения токов, напряжения на катушке и емкости.
Решение:
1. Рассмотрим СУР.
Источник отключен: 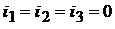 ;
; 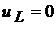 ;
; 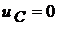 .
.
В конце СУР: 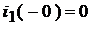 ;
; 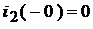 ;
; 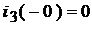 ;
; 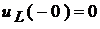 ;
;  .
.
2. Зафиксируем ННУ: 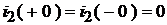 ,
, 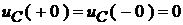 .
.
 Рис. 1.66
Рис. 1.66
|
3. Определим ЗНУ: в расчетной схеме, сформированной для момента времени 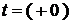 , по первому закону коммутации индуктивность разрывает ветвь, а по второму закону коммутации емкость закорачивает (рис. 1.66):
, по первому закону коммутации индуктивность разрывает ветвь, а по второму закону коммутации емкость закорачивает (рис. 1.66):
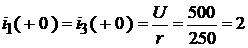 ;
;
 ;
;
Определим начальные значения производных для токов и напряжений.
Из дифференциальных соотношений  и
и  найдем начальные значения двух производных:
найдем начальные значения двух производных:
 .
.
 .
.
Начальные значения производных от других функций определим из системы уравнений Кирхгофа послекоммутационной схемы. Система переписывается для производных, фиксируется для момента времени 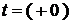 и подставляются уже найденные ранее значения
и подставляются уже найденные ранее значения 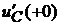 и
и 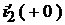 .
.
 →
→  →
→ 
Решая последнюю систему, находим:
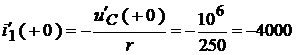 ,
,
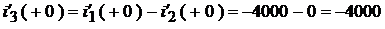 .
.
Итак, мы зафиксировали начальные значения всех функций и их производных.
4. Рассчитаем НУР постоянного тока (рис.1.67):
 Рис. 1.67
Рис. 1.67
|
 ;
; 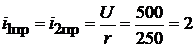 ;
;
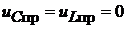 ;
; 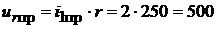 .
.
Начальные значения принужденных составляющих − те же самые величины 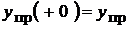 .
.
|
|
|
5. Составим характеристическое уравнение и найдем его корень (рис. 1.68):
 Рис. 1.68
Рис. 1.68
|
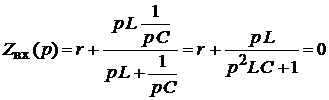 ,
,
или: 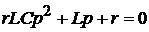 ,
,
т. е: 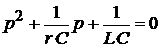 .
.
Решая уравнение, нашли:

Таким образом:  ;
;  .
.
Корни характеристического уравнения − действительные и различные.
Постоянная времени и длительность переходного процесса равна:
 ,
,  .
.
6. Запишем общее решение для  и его производной
и его производной  :
:

7. Система уравнений для расчета постоянных интегрирования ( в общих обозначениях):
После подстановки начальных условий, получим:
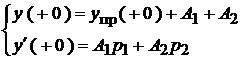
Такая система обрабатывается для каждой конкретной функции. Две постоянные 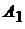 и
и 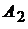 для функции являются результатом решения этой системы.
для функции являются результатом решения этой системы.
8. Расчет постоянных интегрирования и решения для всех переходных функций:
Ток 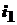 :
: 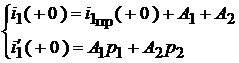 или
или 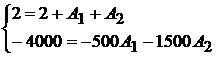
Решая совместно два уравнения, получаем: 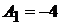 и
и 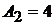 .
.
Следовательно, ток 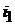 равен:
равен:
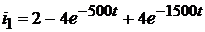 .
.
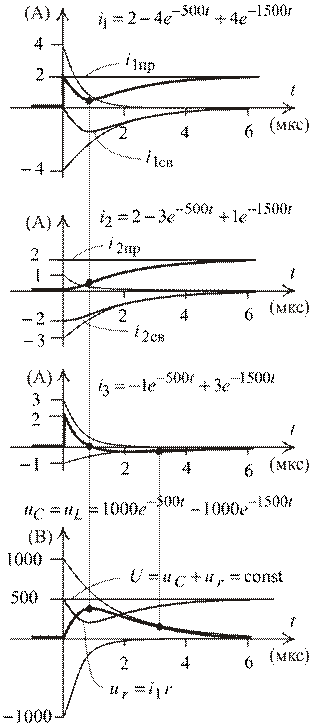 Рис. 1.69
Рис. 1.69
|
Ток 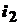 :
: 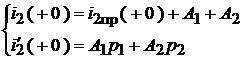 или
или 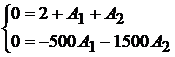
Отсюда получаем: 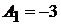 и
и 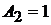 .
.
Следовательно, ток 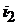 равен:
равен:
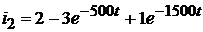 .
.
Ток 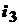 :
: 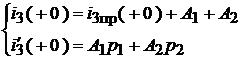 или
или 
Отсюда получаем:  и
и  .
.
Следовательно, ток  равен:
равен:
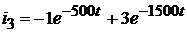 .
.
Напряжение 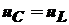 :
:
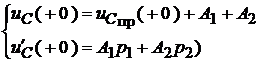
или 
Отсюда получаем:  и
и 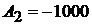 .
.
Следовательно, напряжение равно:
|
|
|
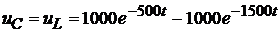 .
.
Напряжение 
 .
.
9. Графики переходных функций в масштабе представлены на рис. 1.69. Здесь показаны слагаемые экспонент свободных функций, сами свободные функции и принужденные составляющие, если они имеются в решении. Характерные точки дифференциально-связанных функций совмещены по времени. Визуально просматриваются уравнения, записанные по законам Кирхгофа.
Задача 2. Переходный процесс в цепи второго порядка с постоянным источником питания и кратными корнями характеристического уравнения.
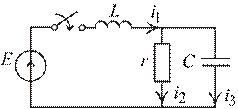 Рис. 1.70
Рис. 1.70
|
Условие:
 (В);
(В); 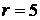 (Ом);
(Ом);
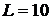 (мГн);
(мГн); 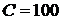 (мкФ).
(мкФ).
Определить мгновенные значения токов, напряжения на катушке и емкости.
Решение:
1. Рассмотрим СУР.
Источник отключен: 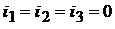 ;
; 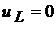 ;
; 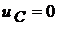 .
.
В конце СУР: 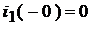 ;
; 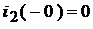 ;
; 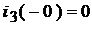 ;
; 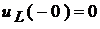 ;
;  .
.
2. Зафиксируем ННУ: 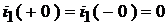 ,
, 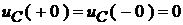 .
.
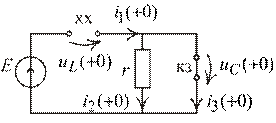 Рис. 1.71
Рис. 1.71
|
3. Определим ЗНУ: в расчетной схеме, сформированной для момента времени 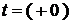 , по первому закону коммутации индуктивность разрывает ветвь, а по второму закону коммутации емкость закорачивает (рис. 1.71):
, по первому закону коммутации индуктивность разрывает ветвь, а по второму закону коммутации емкость закорачивает (рис. 1.71):
 ;
;
 ;
;
Определим начальные значения производных для токов и напряжений.
Из дифференциальных соотношений  и
и  найдем начальные значения двух производных:
найдем начальные значения двух производных:
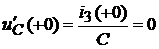 .
.
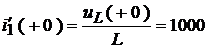 .
.
Начальные значения производных от других функций определим из системы уравнений Кирхгофа послекоммутационной схемы. Система переписывается для производных, фиксируется для момента времени 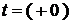 и подставляются уже найденные ранее значения
и подставляются уже найденные ранее значения 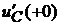 и
и 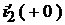 .
.
|
|
|
 →
→ 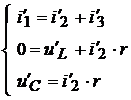 →
→ 
Решая последнюю систему, находим:
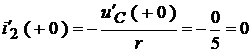 ,
,
 .
.
Итак, мы зафиксировали начальные значения всех функций и их производных.
4. Рассчитаем НУР постоянного тока (рис.1.72):
 Рис. 1.72
Рис. 1.72
|
 ;
;
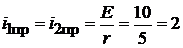
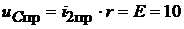 ;
;
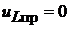 .
.
Начальные значения принужденных составляющих − те же самые величины 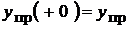 .
.
5. Составим характеристическое уравнение и найдем его корень (рис. 1.73):
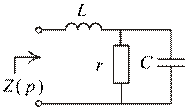 Рис. 1.73
Рис. 1.73
|
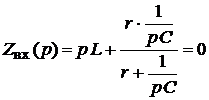 ,
,
Решая данное уравнение, нашли:
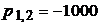 .
.
Корни характеристического уравнения − действительные и различные.
Постоянная времени и длительность переходного процесса равна:
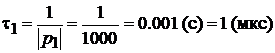 ,
, 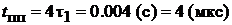 .
.
6. Запишем общее решение для  и его производной
и его производной  :
:
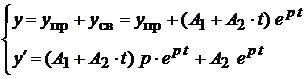
7. Система уравнений для расчета постоянных интегрирования ( в общих обозначениях):
После подстановки начальных условий, получим:
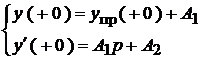
Такая система обрабатывается для каждой конкретной функции. Две постоянные 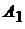 и
и 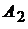 для функции являются результатом решения этой системы.
для функции являются результатом решения этой системы.
8. Расчет постоянных интегрирования и решения для всех переходных функций:
|
|
|
Ток 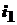 :
:
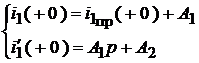 или
или 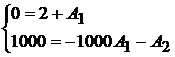
Решая совместно два уравнения, получаем: 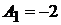 и
и 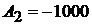 .
.
Следовательно, ток 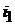 равен:
равен:
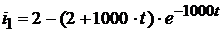 .
.
Остальные функции определим, исходя из зависимостей 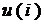 на элементах цепи и из уравнений Кирхгофа:
на элементах цепи и из уравнений Кирхгофа:
Напряжение 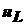 :
:
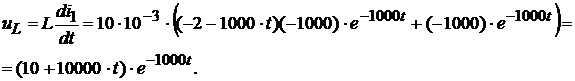
Следовательно, напряжение  равно:
равно:
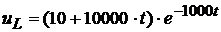 .
.
Ток 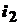 :
:
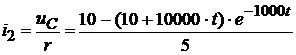
Следовательно, ток 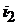 равен:
равен:
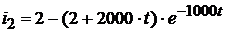 .
.
Ток 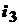 :
:
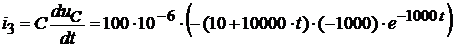
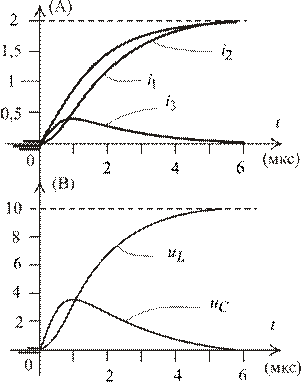 Рис. 1.74
Рис. 1.74
|
Следовательно, ток  равен:
равен:
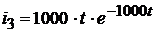 .
.
Напряжение 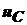 :
:
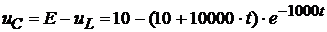 .
.
Напряжение 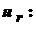

При расчете таким образом, остается возможность проверки по начальным и установившимся значениям токов.
9. Графики переходных функций в масштабе представлены на рис. 1.74. Здесь показаны слагаемые экспонент свободных функций, сами свободные функции и принужденные составляющие, если они имеются в решении. Характерные точки дифференциально-связанных функций совмещены по времени. Визуально просматриваются уравнения, записанные по законам Кирхгофа.
Задача 3. Переходный процесс в цепи второго порядка с постоянным источником питания и комплексно-сопряженными корнями характеристического уравнения.
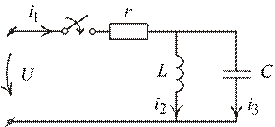 Рис. 1.75
Рис. 1.75
|
 В;
В;
 Ом;
Ом; 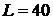 мГн;
мГн; 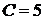 мкФ.
мкФ.
Определить мгновенные значения токов, напряжения на катушке и емкости.
Решение:
1. Рассмотрим СУР.
Источник отключен: 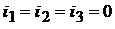 ;
; 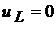 ;
; 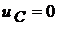 .
.
В конце СУР: 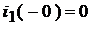 ;
; 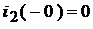 ;
; 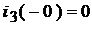 ;
; 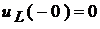 ;
;  .
.
2. Зафиксируем ННУ: 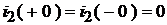 ,
, 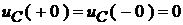 .
.
 Рис. 1.76
Рис. 1.76
|
3. Определим ЗНУ: в расчетной схеме, сформированной для момента времени 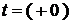 , по первому закону коммутации индуктивность разрывает ветвь, а по второму закону коммутации емкость закорачивает (рис. 1.76):
, по первому закону коммутации индуктивность разрывает ветвь, а по второму закону коммутации емкость закорачивает (рис. 1.76):
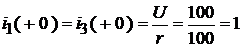 ;
;
 ;
;
Определим начальные значения производных для токов и напряжений.
Из дифференциальных соотношений  и
и  найдем начальные значения двух производных:
найдем начальные значения двух производных:
 .
.
 .
.
Начальные значения производных от других функций определим из системы уравнений Кирхгофа послекоммутационной схемы. Система переписывается для производных, фиксируется для момента времени 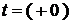 и подставляются уже найденные ранее значения
и подставляются уже найденные ранее значения 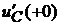 и
и 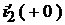 .
.
 →
→  →
→ 
Решая последнюю систему, находим:
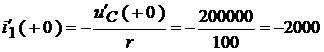 ,
,
 .
.
Итак, мы зафиксировали начальные значения всех функций и их производных.
4. Рассчитаем НУР постоянного тока (рис. 1.77):
 Рис. 1.77
Рис. 1.77
|
 ;
; 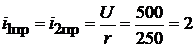 ;
;
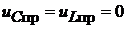 ;
; 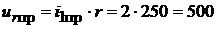 .
.
Начальные значения принужденных составляющих − те же самые величины 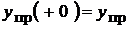 .
.
5. Составим характеристическое уравнение и найдем его корень (рис. 1.78):
 Рис. 1.78
Рис. 1.78
|
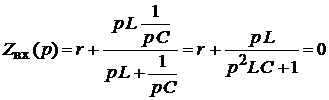 ,
,
или: 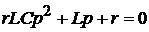 ,
,
т. е: 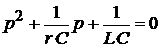 .
.
Решая уравнение, нашли:

здесь: 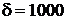 ,
, 
Таким образом:  ;
;  .
.
Корни характеристического уравнения − комплексно−сопряженные.
здесь: 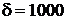 ,
, 
Постоянная времени и длительность переходного процесса равна:
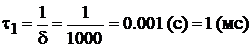 ,
, 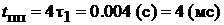 .
.
6. Запишем общее решение для  и его производной
и его производной  :
:

7. Система уравнений для расчета постоянных интегрирования (в общих обозначениях):
После подстановки начальных условий, получим:
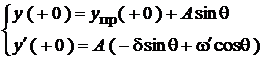
Такая система обрабатывается для каждой конкретной функции. Две постоянные 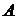 и
и 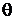 для функции являются результатом решения этой системы.
для функции являются результатом решения этой системы.
8. Расчет постоянных интегрирования и решения для всех переходных функций:
Ток 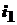 :
:
 или
или 
Решая совместно два уравнения, получаем: 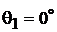 и
и  .
.
Следовательно, ток 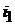 равен:
равен:
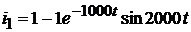 .
.
Ток 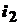 :
:
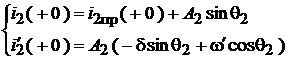 или
или 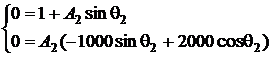
Отсюда получаем: 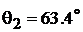 и
и 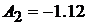 .
.
Следовательно, ток 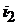 равен:
равен:
 .
.
Ток 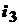 :
:
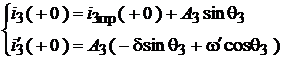 или
или 
Отсюда получаем: 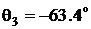 и
и 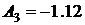 .
.
Следовательно, ток  равен:
равен:
 .
.
Напряжение 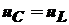 :
:
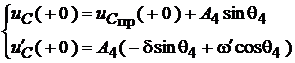 или
или 
Отсюда получаем:  и
и 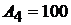 .
.
Следовательно, напряжение 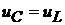 равно:
равно:
 .
.
Напряжение 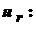
 .
.
9. Построим графики для найденных функций (рис. 1.79).
Период колебания  с.
с.
Путем пропорционального перерасчета начальные фазы, можно выразить в радианах или в долях 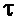 . Например для
. Например для 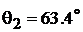 :
:
Начальная фаза в секундах:
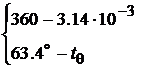 →
→ 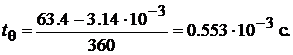
Начальная фаза в долях 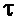 :
: 
 Рис. 1.79
Рис. 1.79
|
Задача 4. Переходный процесс в цепи второго порядка с синусоидальным источником ЭДС и с двумя индуктивностями.
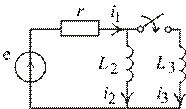 Рис. 1.80
Рис. 1.80
|
Условия:
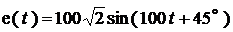 (В);
(В);
 (Ом);
(Ом);
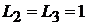 (Гн).
(Гн).
Определить закон изменения тока 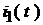 ,
, 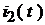 ,
, 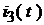 .
.
Решение:
1. Рассмотрим СУР.
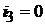 ,
,
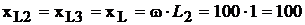 ,
,
 ,
,
 ,
,
В конце СУР:
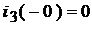 ;
;
 .
.
2. Зафиксируем ННУ: 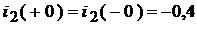 ;
;
 .
.
3. Определим ЗНУ для искомого тока по схеме замещения
(рис. 1.49) для момента времени 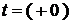 .
.
Начальные значения источника ЭДС:
 .
.
4. По первому закону коммутации индуктивность 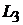 разрывает
разрывает
ветвь, а индуктивность 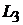 заменяется источником тока (рис. 1.81):
заменяется источником тока (рис. 1.81):
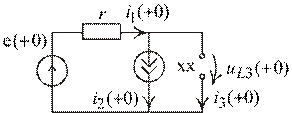 Рис. 1.81
Рис. 1.81
|
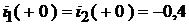 ;
;

Определим начальные значения производных для токов и напряжений.
Из дифференциального соотношения  найдем начальные значения двух производных:
найдем начальные значения двух производных:
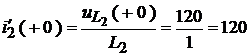 ,
,
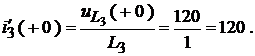
Начальные значения производных от других функций определим из системы уравнений Кирхгофа послекоммутационной схемы. Система переписывается для производных, фиксируется для момента времени 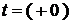 и подставляются уже найденные ранее значения
и подставляются уже найденные ранее значения 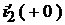 и
и  .
.
 →
→ 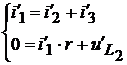 →
→ 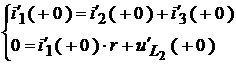
Решая последнюю систему, находим:
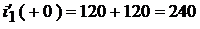 ,
,
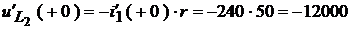 .
.
5. Рассчитаем НУР синусоидального тока. Принужденные составляющие искомых функций – частное решение неоднородного дифференциального уравнения – определим в виде синусоидальных токов, определяемых источником в послекоммутационной схеме:
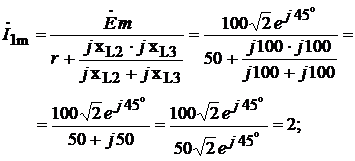
Мгновенные значения для токов:
 ;
; 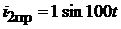 ;
; 
Как будет видно из дальнейшего расчета для токов, новый установившийся режим формируется не только этими частными решениями.
6. Составим характеристическое уравнение и найдем его корень.
Сведем систему уравнений Кирхгофа нашей схемы к одному уравнению для тока 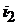 :
:

Продифференцируем второе уравнение и с учетом первого уравнения системы, запишем:
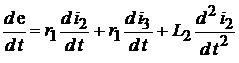 .
.
Из третьего уравнения следует, что: 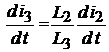 . Значит:
. Значит:
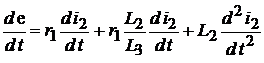
или:

Для того, чтобы составить характеристическое уравнение цепи, отбросим правую часть и осуществим алгебраизацию однородного уравнения.
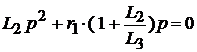 ,
,
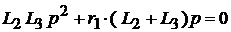 .
.
Мы проделали эту работу для Вас, читатель, чтобы убедительнее выглядели некоторые нижеследующие заключения.
Определим корни характеристического уравнения:
 ,
,
Решая уравнение, нашли:
 ;
;
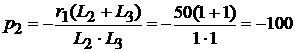 .
.
Обратим внимание на то, что при формировании характеристического уравнения из структуры  не следует сокращать числитель и знаменатель конструкции на общий множитель
не следует сокращать числитель и знаменатель конструкции на общий множитель 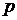 . Это привело бы к потере нулевого корня характеристического уравнения, то есть к потере постоянной составляющей в свободной функции
. Это привело бы к потере нулевого корня характеристического уравнения, то есть к потере постоянной составляющей в свободной функции
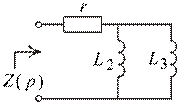 Рис. 1.82
Рис. 1.82
|
При естественной обработке схемы выражение 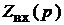 приводят к общему знаменателю, а общий множитель слагаемых числителя
приводят к общему знаменателю, а общий множитель слагаемых числителя 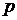 выносят за скобки.
выносят за скобки.
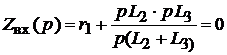 ,
,
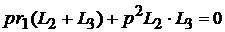 .
.
Получается то же самое характеристическое уравнение с одним нулевым корнем. Если во втором слагаемом выражения 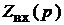 сократить числитель и знаменатель на общий множитель
сократить числитель и знаменатель на общий множитель 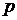 , то получится конструкция
, то получится конструкция  , где потерян нулевой корень, и которая уже не может служить характеристическим уравнением цепи.
, где потерян нулевой корень, и которая уже не может служить характеристическим уравнением цепи.
По той же причине при определении порядка цепи не следует объединять параллельные индуктивности. Это привело бы к потери сверхпроводящего индуктивного контура, а понижение порядка уравнения – к потере постоянной составляющей тока в этом контуре, которая является специфической особенностью рассматриваемой схемы.
7. Расчет токов в переходном режиме:
Корни характеристического уравнения действительные различные.
Решение в общем виде для свободной составляющей запишем в виде суммы двух экспонент.
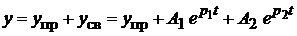 ,
,
или для тока 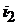 :
:
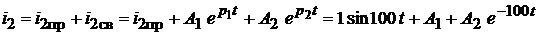 .
.
для определения постоянных интегрирования запишем производную этой функции:
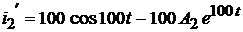 .
.
В полученные выражения подставим начальные условия : 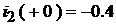 и
и 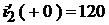 . Получим систему алгебраических уравнений с неизвестными постоянными
. Получим систему алгебраических уравнений с неизвестными постоянными 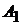 и
и  .
.
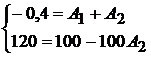
Решая совместно два уравнения, получаем: 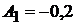 и
и 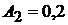 .
.
Следовательно, ток 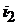 равен:
равен:
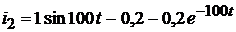 .
.
Токи 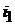 и
и 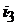 найдем также как результат интегрирования системы уравнений цепи:
найдем также как результат интегрирования системы уравнений цепи:
Ток 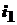 :
: 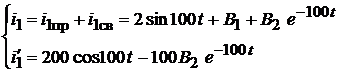
Известно, что 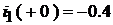 и
и 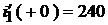 . Следовательно, мы также получим систему алгебраических уравнений с неизвестными постоянными
. Следовательно, мы также получим систему алгебраических уравнений с неизвестными постоянными 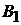 и
и  .
.
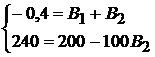
Решая совместно два уравнения, получаем: 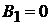 и
и 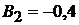 .
.
Следовательно, ток 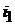 равен:
равен:
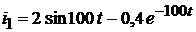 .
.
Ток 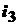 :
: 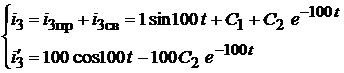
Также известно, что 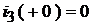 и
и 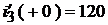 . Следовательно, мы снова получим систему алгебраических уравнений с неизвестными постоянными
. Следовательно, мы снова получим систему алгебраических уравнений с неизвестными постоянными 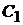 и
и 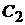 .
.
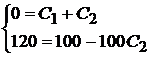
Решая совместно два уравнения, получаем: 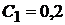 и
и 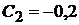 .
.
Следовательно, ток 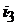 равен:
равен:
 .
.
После расчета переходных функций в таком виде, остается возможность проверки полученных решений по независимым законам Кирхгофа.
8. Построим график для найденной функциитоков (рис. 1.83):
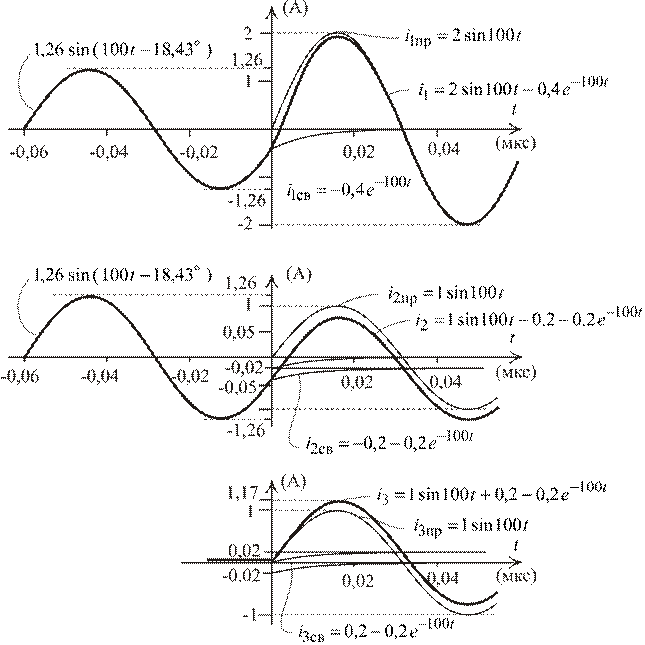 Рис. 1.83
Рис. 1.83
|
Заданные параметры таковы, что период колебаний равен  с, постоянная времени:
с, постоянная времени: 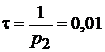 с, свободные экспоненты затухают где-то за
с, свободные экспоненты затухают где-то за 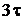 , то есть приблизительно за полпериода колебаний.
, то есть приблизительно за полпериода колебаний.
Как видно, для токов 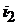 и
и 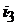 новый установившийся режим формируется двумя первыми слагаемыми решения, то есть принужденной синусоидальной составляющей и свободной постоянной составляющей. И только в решении для тока
новый установившийся режим формируется двумя первыми слагаемыми решения, то есть принужденной синусоидальной составляющей и свободной постоянной составляющей. И только в решении для тока 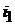 он является синусоидальной функцией.
он является синусоидальной функцией.
Дата добавления: 2018-06-27; просмотров: 837; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
