Точечные оценки параметров распределения
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Юго-Западный государственный университет»
(ЮЗГУ)
Кафедра высшей математики
УТВЕРЖДАЮ
Проректор по учебной работе
___________О.Г. Локтионова
«____»_____________2018 г.
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Методические указания по выполнению модуля «Элементы математической статистики и корреляционного анализа»
Курск 2018
УДК 519.22
Составители: О.А. Бредихина, С.В. Шеставина
Рецензент
Кандидат технических наук, доцент кафедры высшей математики Н.А. Моргунова
Элементы математической статистики: методические указания по выполнению модуля «Элементы математической статистики и корреляционного анализа» / Юго-Зап. гос. ун-т; сост.: О.А. Бредихина, С.В. Шеставина. – Курск, 2018. – 28 с.
Методические указания содержат теоретические сведения по теме «Элементы математической статистики», подробно разобраны типовые задачи.
Методические указания предназначены для студентов всех направлений и специальностей, изучающих математическую статистику.
|
|
|
Текст печатается в авторской редакции
Подписано в печать ___________. Формат 60х84 1/16.
Усл. печ. л. . Уч.-изд. л. . Тираж экз. Заказ . Бесплатно.
Юго-западный государственный университет.
305040 Курск, ул. 50 лет Октября, 94.
Содержание
Введение………………………………………………………………..4
1. Статистическое распределение выборки. Графическое изображение вариационных рядов……………………………………5
2. Точечные оценки параметров распределения……………………11
3. Интервальные оценки параметров распределения………………18
4. Доверительный интервал для оценки математического ожидания нормально распределённой случайной величины при известном среднеквадратическом отклонении…………………………….……20
5. Доверительный интервал для оценки математического ожидания нормально распределённой случайной величины при неизвестном среднеквадратическом отклонении………………………………….22
6. Проверка статистических гипотез………………………….……..24
Список рекомендуемой литературы...................................................28
Введение
В образовательном процессе математическая статистика традиционно считается наиболее сложным для восприятия предметом. Предлагаемая работа ставит своей целью помочь тем, кто осваивает этот раздел математики.
|
|
|
В ней содержатся основные положения математической статистики, а также разобраны задачи с подробным решением по указанной тематике.
Данное пособие является приложением к модулю 20 «Элементы математической статистики и корреляционного анализа».
Авторы надеются, что это методическое издание поможет студентам в самостоятельной работе по выполнению модуля и изучению данного материала.
Статистическое распределение выборки.
Графическое изображение вариационных рядов
Пусть из генеральной совокупности извлечена выборка объёма n, в которой значения 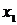 некоторого исследуемого признака
некоторого исследуемого признака  наблюдалось
наблюдалось 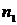 раз, значения
раз, значения 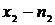 раз, значения
раз, значения 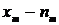 раз. Значения
раз. Значения 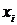 называются вариантами, а
называются вариантами, а 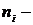 их частотами.
их частотами.
Вариационным рядом называется ранжированный в порядке возрастания (или убывания) ряд вариант с соответствующими им частотами.
Отношения частот вариант к объёму выборки
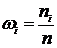
называются относительными частотами. При этом 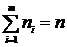 .
.
Перечень вариант и соответствующих им частот (относительных частот) называется статистическим распределением выборки или статистическим рядом. Здесь имеется аналогия с законом распределения случайной величины: в теории вероятностей – это соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике – это соответствие между наблюдаемыми вариантами и их частотами (относительными частотами). Заметим, что сумма относительных частот равна единице, т. е.  .
.
|
|
|
Вариационный ряд называется дискретным, если любые его варианты отличаются на постоянную величину, и непрерывным (интервальным), если варианты могут отличаться один от другого на сколь угодно малую величину.
Для преобразования дискретного статистического ряда в интервальный необходимо установить величину интервалов, получить шкалу интервалов и в соответствии с этой шкалой сгруппировать данные.
Для определения величины интервала используется формула Стерджесса:
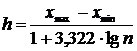 ,
,
где 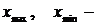 наибольшее и наименьшее значения признака;
наибольшее и наименьшее значения признака;
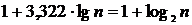 – число интервалов.
– число интервалов.
Шкала интервалов формируется следующим образом:
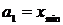 ,
,
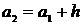 ,
,
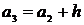 ,
,
…
Границы интервалов формируются до тех пор, пока не превысят 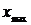 :
:  ,
, 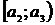 , …,
, …, 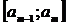 , где
, где 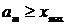 .
.
Во второй строке статистического ряда записывается количество наблюдений, попавших в каждый интервал.
Для изображения вариационных рядов обычно используются полигон, гистограмма, кумулятивная кривая.
|
|
|
1. Дискретный вариационный ряд графически изображается полигоном.
Каждую пару значений 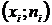 из распределения выборки можно трактовать как точку на координатной плоскости. Точно так же можно рассматривать и пары значений
из распределения выборки можно трактовать как точку на координатной плоскости. Точно так же можно рассматривать и пары значений 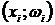 относительного распределения выборки.
относительного распределения выборки.
Полигоном частот называется ломаная, отрезки которой соединяют точки 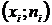 .
.
Полигоном относительных частот называется ломаная, отрезки которой соединяют точки 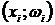 .
.
2. Интервальный вариационный ряд графически изображается гистограммой.
Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению 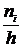 (плотность частоты).
(плотность частоты).
Геометрический смысл гистограммы частот: площадь гистограммы частот равна сумме всех частот, т.е. объёму выборки n.
Гистограммой относительных частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению 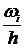 (плотность относительной частоты).
(плотность относительной частоты).
Геометрический смысл гистограммы относительных частот: площадь гистограммы относительных частот равна сумме всех частот, т.е. единице.
3.Кумулятивная кривая (кумулята, кривая накопленных частот (относительных частот)) строится как для дискретных, так и для интервальных вариационных рядов.
Для дискретных вариационных рядов кумулятивная кривая – ломаная, соединяющая точки  или
или 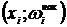 ,
, 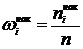 , где
, где  накопленная частота.
накопленная частота.
Для интервального вариационного ряда по оси абсцисс откладываются интервалы. Верхним границам интервалов соответствуют накопленные частоты, а нижней границе первого интервала – накопленная частота, равная нулю.
Пример решения задания 1
Имеются данные о стаже рабочих цеха: 6, 6, 10, 10, 7, 2, 2, 5, 8, 8, 12, 9, 10, 10, 7, 7, 6, 7, 2, 3. Построить дискретный и интервальный вариационные ряды и изобразить их графически: построить полигон, гистограмму, кумулятивную кривую.
Решение
1) Построение дискретного вариационного ряда.
Находится объём выборки, то есть 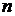 – общее количество чисел (у нас
– общее количество чисел (у нас 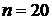 ).
).
Составляется таблица, где 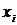 – варианты (числа из условия), расположенные в порядке возрастания,
– варианты (числа из условия), расположенные в порядке возрастания, 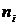 – сколько раз встречается каждое число.
– сколько раз встречается каждое число.
Дискретный вариационный ряд
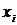
| 2 | 3 | 5 | 6 | 7 | 8 | 9 | 10 | 12 |
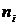
| 3 | 1 | 1 | 3 | 4 | 2 | 1 | 4 | 1 |
Контроль: 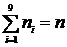 , то есть 3+1+1+3+4+2+1+4+1=20 – верно.
, то есть 3+1+1+3+4+2+1+4+1=20 – верно.
2) Построение интервального вариационного ряда
Находится величина интервала:
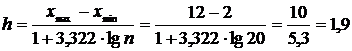 .
.
Округление величины 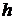 производится следующим образом: если в условии даны числа, большие 100, то округляем до целых, если числа до 100, то оставляем один знак после запятой, а если даны очень маленькие числа, то округляем до сотых.
производится следующим образом: если в условии даны числа, большие 100, то округляем до целых, если числа до 100, то оставляем один знак после запятой, а если даны очень маленькие числа, то округляем до сотых.
Далее шкала интервалов формируется так:
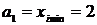 ,
,
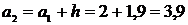 ,
,
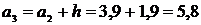 ,
,
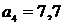 ,
,
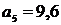 ,
,
 ,
,
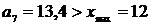 .
.
Составляется таблица, в которой первая строка имеет вид: 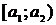 ,
, 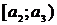 , …
, … 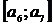 . Вторая строка формируется так:
. Вторая строка формируется так: 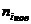 – общая сумма частоты встреч всех чисел дискретного ряда, попадающих в соответствующий интервал.
– общая сумма частоты встреч всех чисел дискретного ряда, попадающих в соответствующий интервал.
Интервальный вариационный ряд
| Интервал | 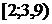
| 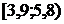
| 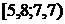
| 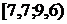
| 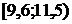
| 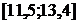
|
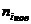
| 3+1=4 | 1 | 3+4=7 | 2+1=3 | 4 | 1 |
3) Построение полигона частот по дискретному вариационному ряду.
Дискретный вариационный ряд имеет вид:
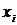
| 2 | 3 | 5 | 6 | 7 | 8 | 9 | 10 | 12 |
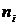
| 3 | 1 | 1 | 3 | 4 | 2 | 1 | 4 | 1 |
Соединив точки с координатами 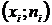 , получим искомый график.
, получим искомый график.
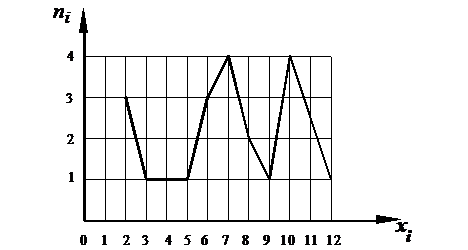
Рис. 1 Полигон частот
4) Построение гистограммы частот по интервальному вариационному ряду.
Дополним интервальный вариационный ряд. Последняя строка таблицы необходима для дальнейшего построения гистограммы частот.
| Интервал | 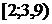
| 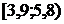
| 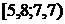
| 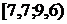
| 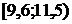
| 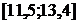
|
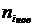
| 4 | 1 | 7 | 3 | 4 | 1 |
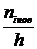
| 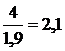
| 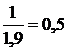
| 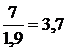
| 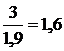
| 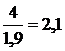
| 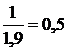
|

Рис. 2 Гистограмма частот
5) Построение кумулятивной кривой для дискретного вариационного ряда.
Дополним дискретный вариационный ряд. Последняя строка таблицы необходима для дальнейшего построения кумулятивной кривой.
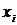
| 2 | 3 | 5 | 6 | 7 | 8 | 9 | 10 | 12 |
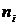
| 3 | 1 | 1 | 3 | 4 | 2 | 1 | 4 | 1 |
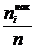
| 0,15 | 0,20 | 0,25 | 0,40 | 0,60 | 0,70 | 0,75 | 0,95 | 1 |

Рис. 3 Кумулятивная кривая для дискретного вариационного ряда
6) Построение кумулятивной кривой для интервального вариационного ряда.
| Интервал | 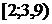
| 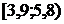
| 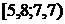
| 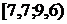
| 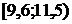
| 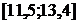
|
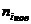
| 4 | 1 | 7 | 3 | 4 | 1 |
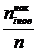
| 0,20 | 0,25 | 0,60 | 0,75 | 0,95 | 1 |
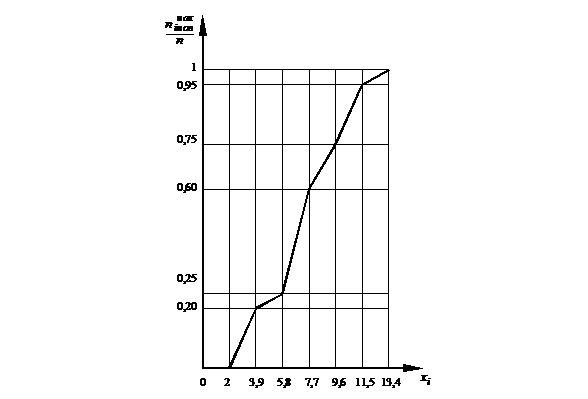
Рис. 4 Кумулятивная кривая для интервального вариационного ряда
Точечные оценки параметров распределения
Числовые характеристики всей генеральной совокупности называются параметрами. Так как всю генеральную совокупность изучить достаточно часто не представляется возможным, о параметрах судят по выборочным характеристикам.
На основании выборочных данных можно получить лишь приближенное значение параметра, которое является его оценкой.
Обозначим 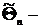 точечная оценка для параметра
точечная оценка для параметра 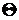 генеральной совокупности.
генеральной совокупности.
Многократные выборки одинакового объёма дадут различные значения параметра 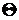 . В этом случае возникает проблема выбора наилучшей оценки. Чтобы выбранная оценка была наилучшей, она должна удовлетворять свойствам несмещённости, эффективности и состоятельности.
. В этом случае возникает проблема выбора наилучшей оценки. Чтобы выбранная оценка была наилучшей, она должна удовлетворять свойствам несмещённости, эффективности и состоятельности.
1. Оценка 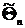 называется несмещённой, если её математическое ожидание равно оцениваемому параметру, т.е.
называется несмещённой, если её математическое ожидание равно оцениваемому параметру, т.е. 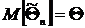 .
.
2. 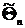 называется эффективной, если она имеет наименьшую дисперсию при заданном объёме выборки.
называется эффективной, если она имеет наименьшую дисперсию при заданном объёме выборки.
3. Состоятельной называется оценка, которая при 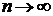 стремится по вероятности к оцениваемому параметру
стремится по вероятности к оцениваемому параметру 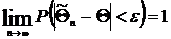 .
.
Репрезентативная выборка – это такая выборка, в которой все основные признаки генеральной совокупности, из которой извлечена данная выборка, представлены приблизительно в той же пропорции или с той же частотой, с которой данный признак выступает в этой генеральной совокупности. При достаточно большом значении объёма выборки нет разницы в выборе смещённой или несмещённой оценки параметра, при малом n необходимо рассматривать несмещённую оценку, поскольку выборка будет репрезентативной, то есть полностью представлять генеральную совокупность.
Для выборки можно определить ряд числовых характеристик: выборочное среднее, выборочная дисперсия, выборочное среднеквадратическое отклонение, размах выборки, асимметрия, эксцесс.
Пусть статистическое распределение выборки объёма n имеет вид:
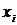
| 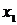
| 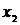
| 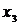
| … | 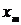
|
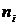
| 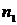
| 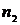
| 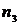
| … | 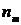
|
1) Выборочное среднее (обозначается 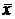 ) – это среднее арифметическое всех значений выборки:
) – это среднее арифметическое всех значений выборки:
 или
или 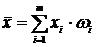 .
.
Выборочное среднее показывает среднее значение, вокруг которого группируются варианты. 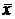 является несмещённой и состоятельной оценкой математического ожидания.
является несмещённой и состоятельной оценкой математического ожидания.
Свойства средней арифметической 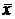 :
:
1. 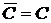 , где С – постоянная;
, где С – постоянная;
2. 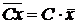 ;
;
3. 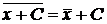 ;
;
4. 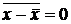 ;
;
5. 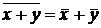 .
.
2) Выборочная дисперсия – это среднее арифметическое квадратов отклонений значений выборки от выборочной средней.
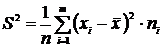 .
.
Выборочная дисперсия показывает меру разброса данных вокруг среднего значения. Она является состоятельной и смещённой оценкой дисперсии.
Свойства средней арифметической 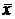 :
:
1.  , где С – постоянная;
, где С – постоянная;
2. 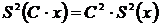 ;
;
3. 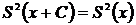 ;
;
4. 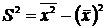 , где
, где 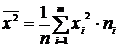
Алгоритм расчёта выборочной дисперсии
1) Вычисляется объём выборки n;
2) Находится выборочная средняя 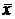 ;
;
3) Определяется величина 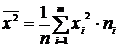 ;
;
4) 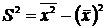 .
.
Для оценки степени отклонения от среднего значения удобно иметь дело с величиной той же размерности, что и величина Х. Для этого вводится понятие выборочного среднеквадратического отклонения.
3) Выборочное среднеквадратической отклонение – это арифметическое значение корня квадратного из его дисперсии, т.е.
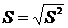 .
.
4) Размах выборки (обозначается 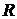 ) – это разность между максимальной и минимальной вариантами или длина интервала, которому принадлежат все варианты выборки:
) – это разность между максимальной и минимальной вариантами или длина интервала, которому принадлежат все варианты выборки:
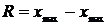 .
.
Для подробного описания особенностей распределения используют дополнительные характеристики – моменты распределения. Выяснение общего характера предполагает не только оценку степени его однородности, но и позволяет исследовать форму распределения.
Средняя из k-х степеней отклонений вариант 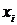 от некоторой постоянной величины
от некоторой постоянной величины 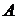 называется моментом k-го порядка:
называется моментом k-го порядка:
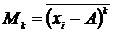 .
.
При расчёте средних в качестве весов можно использовать частоты, относительные частоты или вероятности. При использовании в качестве весов частот или относительных частот моменты называются эмпирическими (обозначаются 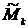 ), а при использовании вероятностей – теоретическими (обозначаются
), а при использовании вероятностей – теоретическими (обозначаются 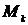 ). Порядок момента определяется величиной k.
). Порядок момента определяется величиной k.
Эмпирический момент k-го порядка – это отношение суммы произведений k-х степеней отклонений вариант от постоянной величины 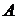 на частоты к объёму выборки:
на частоты к объёму выборки:
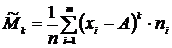 .
.
Практически используют моменты первых четырех порядков. Если 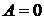 , то моменты начальные;
, то моменты начальные; 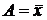 , то моменты центральные;
, то моменты центральные; 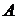 – произвольное число, то моменты условные.
– произвольное число, то моменты условные.
Нормальное распределение является одним из самых распространённых в применениях математической статистики. Для оценки отклонения эмпирического распределения от нормального используются нормированные моменты.
| Порядок момента | Начальные моменты | Центральные моменты | Нормированные моменты |
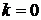
| 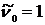
| 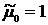
| 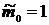
|
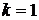
| 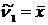
| 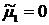
| 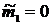
|
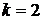
| 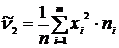
| 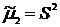
| 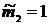
|
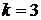
| 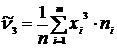
| 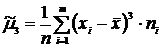
| 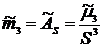
|
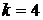
| 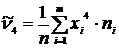
| 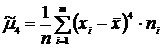
| 
|
| Общие формулы | |||
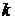
| 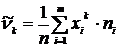
| 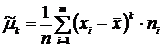
| 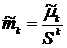
|
Для облегчения расчётов можно воспользоваться соотношениями между начальными и центральными моментами:
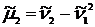 ,
,
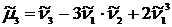 ,
,
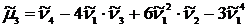 .
.
Из математической статистики известно, что при увеличении объёма статистической совокупности 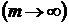 и одновременного уменьшении интервала группировки полигон либо гистограмма распределения всё более и более приближается к некоторой плавной кривой, являющейся для указанных графиков пределом. Эта кривая называется эмпирической кривой распределения и представляет собой графическое изображение в виде непрерывной линии изменения частот, функционально связанного с изменением вариант. В статистике различают следующие виды кривых распределения: одновершинные и многовершинные кривые.
и одновременного уменьшении интервала группировки полигон либо гистограмма распределения всё более и более приближается к некоторой плавной кривой, являющейся для указанных графиков пределом. Эта кривая называется эмпирической кривой распределения и представляет собой графическое изображение в виде непрерывной линии изменения частот, функционально связанного с изменением вариант. В статистике различают следующие виды кривых распределения: одновершинные и многовершинные кривые.
Однородные совокупности описываются одновершинными распределениями. Многовершинность распределения свидетельствует о неоднородности изучаемой совокупности или о некачественном выполнении группировки. Одновершинные кривые распределения делятся на симметричные, умеренно асимметричные и крайне асимметричные.
Распределение называется симметричным, если частоты любых 2-х вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой. Для характеристики асимметрии используют коэффициент асимметрии.
При симметричном распределении варианты, равноудаленные от 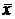 , имеют одинаковую частоту, поэтому каждый центральный момент нечётной степени равен 0. Для несимметричного распределения – не равен 0, следовательно, любой из этих моментов может служить для оценки симметрии. Поэтому выбран нечётный момент наименьшего порядка, не равный нулю или
, имеют одинаковую частоту, поэтому каждый центральный момент нечётной степени равен 0. Для несимметричного распределения – не равен 0, следовательно, любой из этих моментов может служить для оценки симметрии. Поэтому выбран нечётный момент наименьшего порядка, не равный нулю или 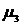 . Чтобы получить безразмерную характеристику, его делят на
. Чтобы получить безразмерную характеристику, его делят на 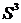 (так как
(так как 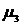 имеет размерность куба рассматриваемой случайной величины).
имеет размерность куба рассматриваемой случайной величины).
5) Коэффициент асимметрии 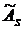 – это отношение центрального момента третьего порядка к кубу выборочного среднеквадратического отклонения:
– это отношение центрального момента третьего порядка к кубу выборочного среднеквадратического отклонения:
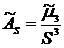 .
.
В одновершинных распределениях величина этого показателя изменяется от –1 до +1. в симметричных распределениях 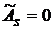 . Если
. Если 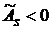 , то имеет место левосторонняя асимметрия, а если
, то имеет место левосторонняя асимметрия, а если 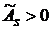 – правосторонняя асимметрия. Чем ближе по модулю
– правосторонняя асимметрия. Чем ближе по модулю 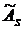 к 1, тем асимметрия существеннее:
к 1, тем асимметрия существеннее:
– если 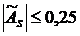 , то асимметрия считается незначительной,
, то асимметрия считается незначительной,
– если 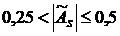 , то асимметрия считается умеренной,
, то асимметрия считается умеренной,
– если 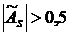 , то асимметрия значительная.
, то асимметрия значительная.
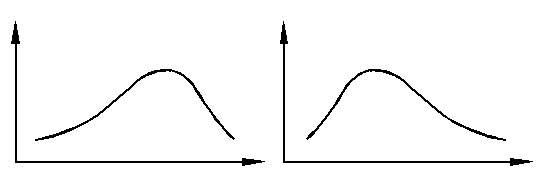
Рис. 5 Правосторонняя Рис. 6 Левосторонняя
асимметрия асимметрия
6) Для нормального распределения 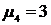 , поэтому для оценки крутизны исследуемого распределения в сравнении с нормальным из
, поэтому для оценки крутизны исследуемого распределения в сравнении с нормальным из 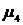 вычитается 3. Эксцесс
вычитается 3. Эксцесс 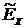 – это уменьшённое на три единицы отношение центрального момента четвёртого порядка к четвёртой степени среднеквадратического отклонения:
– это уменьшённое на три единицы отношение центрального момента четвёртого порядка к четвёртой степени среднеквадратического отклонения:
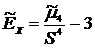 .
.
Кривые распределения, у которых 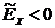 , менее крутые, имеют более плоскую вершину и называются плосковершинными. Кривые распределения, у которых
, менее крутые, имеют более плоскую вершину и называются плосковершинными. Кривые распределения, у которых 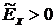 , более крутые, имеют острую вершину и называются островершинными.
, более крутые, имеют острую вершину и называются островершинными.
Рассматривая формулы моментов, можно видеть, что начальный момент первого порядка представляет собой среднюю арифметическую и используется как показатель центра распределения. Центральный момент первого порядка (нулевое свойство средней арифметической) всегда равен нулю. Центральный момент второго порядка представляет собой дисперсию и служит основной мерой колеблемости признака. Центральный момент третьего порядка равен нулю в симметричном распределении и используется для определения показателя асимметрии. Центральный момент четвертого порядка применяется при вычислении показателя эксцесса. Начальные моменты второго, третьего и четвертого порядка, так же как и условные моменты, самостоятельного значения не имеют, а используются для упрощения вычислений центральных моментов.
Пример решения задания 2
Задан вариационный ряд выборки. Найти: выборочное среднее, выборочную дисперсию, выборочное среднеквадратическое отклонение, размах выборки, асимметрию, эксцесс.
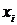
| 3 | 5 | 6 | 8 | 9 | 10 | 14 |
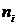
| 2 | 10 | 15 | 20 | 38 | 11 | 4 |
Решение
Объём выборки: 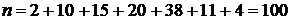 .
.
1) Выборочное среднее:
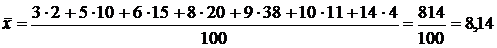 .
.
2) Выборочная дисперсия:
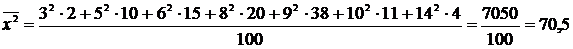 ;
;
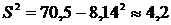 .
.
3) Выборочное среднеквадратическое отклонение:
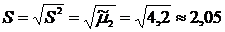 .
.
4) Размах выборки: 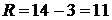 .
.
5) Начальные моменты:
– 1-го порядка 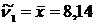 ;
;
– 2-го порядка  ;
;
– 3-го порядка
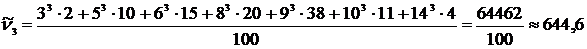 ;
;
– 4-го порядка
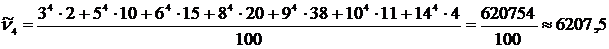 .
.
6) Центральные моменты
– 2-го порядка 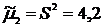 ;
;
– 3-го порядка
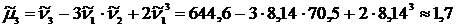 ;
;
– 4-го порядка
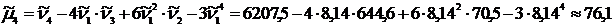 .
.
7) Асимметрия 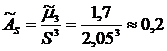 .
.
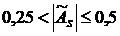 , то есть асимметрия умеренная.
, то есть асимметрия умеренная.
8) Эксцесс 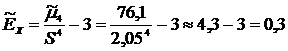 .
.
Так как 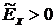 , то кривая распределения является островершинной.
, то кривая распределения является островершинной.
Дата добавления: 2018-06-27; просмотров: 335; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
