Задание 9 № 912 (решено неверно или не решено)
 В правильный четырехугольной пирамиде
В правильный четырехугольной пирамиде 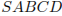 точка
точка  – центр основания,
– центр основания, 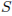 – вершина,
– вершина, 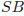 =13,
=13, 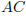 =24. Найдите найдите длину отрезка
=24. Найдите найдите длину отрезка  .
.
Решение.
в правильной пирамиде вершина проецируется в центр основания, следовательно  является высотой пирамиды. тогда по теореме Пифагора
является высотой пирамиды. тогда по теореме Пифагора

Ответ: 5.
Задание 10 № 1016 (решено неверно или не решено)
Максим с папой решил покататься на колесе обозрения. Всего на колесе 30 кабинок, из них 11 – синие, 7 – зеленые, остальные – оранжевые. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Максим прокатится в оранжевой кабинке.
Решение.
на колесе обозрения 30–11–7=12 оранжевых кабинок. Тогда вероятность того, что Максим прокатится в оранжевой кабинке равна
 .
.
Ответ: 0,4.
Задание 11 № 27181 (решено неверно или не решено)
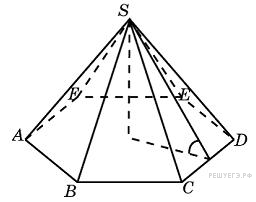 Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 45
Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 45  . Найдите объем пирамиды.
. Найдите объем пирамиды.
Решение.
Вершина правильной пирамиды проецируется в центр ее основания. В правильном шестиугольнике со стороной  расстояние от его центра до стороны равно радиусу вписанной окружности, который равен
расстояние от его центра до стороны равно радиусу вписанной окружности, который равен 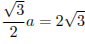 . Так как угол между боковой гранью и основанием равен 45°, высота пирамиды также равна
. Так как угол между боковой гранью и основанием равен 45°, высота пирамиды также равна 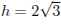 . Тогда имеем:
. Тогда имеем:
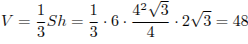 .
.
Ответ: 48.
Задание 12 № 28009 (решено неверно или не решено)
Два тела массой 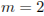 кг каждое, движутся с одинаковой скоростью
кг каждое, движутся с одинаковой скоростью 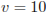 м/с под углом
м/с под углом 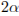 друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении определяется выражением
друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении определяется выражением  . Под каким наименьшим углом
. Под каким наименьшим углом  (в градусах) должны двигаться тела, чтобы в результате соударения выделилось не менее 50 джоулей?
(в градусах) должны двигаться тела, чтобы в результате соударения выделилось не менее 50 джоулей?
Решение.
Задача сводится к решению неравенства  Дж на интервале
Дж на интервале 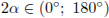 при заданных значениях массы тел
при заданных значениях массы тел 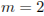 кг и их скоростей
кг и их скоростей 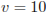 м/с:
м/с:
|
|
|
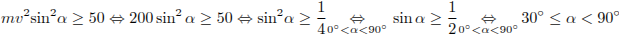 .
.
Значит, наименьший угол 
Ответ: 60.
Задание 13 № 99575 (решено неверно или не решено)
Имеется два сплава. Первый сплав содержит 10% никеля, второй – 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Решение.
Пусть масса первого сплава 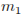 кг, а масса второго –
кг, а масса второго – 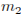 кг. Тогда массовое содержание никеля в первом и втором сплавах
кг. Тогда массовое содержание никеля в первом и втором сплавах 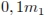 и
и 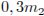 , соответственно. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений:
, соответственно. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений:


Ответ: 100.
Задание 14 № 77489 (решено неверно или не решено)
Найдите точку максимума функции 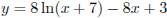 .
.
Решение.
Заметим, что 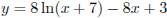 . Область определения функции — открытый луч
. Область определения функции — открытый луч  . Найдем производную заданной функции:
. Найдем производную заданной функции: 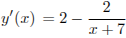 .
.
Найдем производную заданной функции: 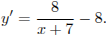
|
|
|
Найдем нули производной: 
Найденная точка лежит на луче  . Определим знаки производной функции и изобразим на рисунке поведение функции:
. Определим знаки производной функции и изобразим на рисунке поведение функции:
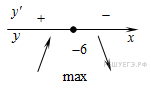
Искомая точка максимума 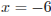 .
.
Ответ: -6.
Проверка части С
Задание С1 № 484550
| Критерии оценивания выполнения задания | Баллы |
| Система решена верно | 2 |
| Тригонометрическое уравнение получено и решено верно, система решена неверно | 1 |
| Все прочие случаи | 0 |
| Максимальный балл | 2 |
Решите систему уравнений 
Решение.
Из неравенства 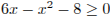 получаем
получаем  .
.
1 случай. Пусть  или
или 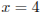 . Если
. Если 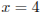 , то
, то 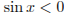 ; если
; если  , то
, то 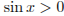 . Из второго уравнения получаем
. Из второго уравнения получаем  , откуда
, откуда 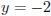 или
или 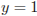 .
.
2 случай. Пусть теперь 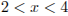 . Тогда
. Тогда 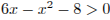 , и поэтому из первого уравнения получаем:
, и поэтому из первого уравнения получаем:  .
.
Учтем, что 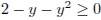 . Тогда
. Тогда 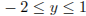 . Из всех решений уравнения
. Из всех решений уравнения  этому условию удовлетворяет только
этому условию удовлетворяет только 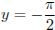 . При этом
. При этом 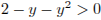 и, из второго уравнения получаем:
и, из второго уравнения получаем: 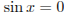 . Из всех решений этого уравнения интервалу
. Из всех решений этого уравнения интервалу 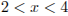 принадлежит только
принадлежит только  . Значит,
. Значит,  ,
, 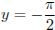 .
.
Ответ: 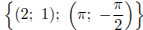 .
.
Задание С2 № 484571
| Содержание критериев оценивания задачи С2 | Баллы |
| Обоснованно получен верный ответ. | 2 |
| Верно описана геометрическая конфигурация, построен или описан геометрический объект, который нужно найти, но получен неверный ответ или решение не закончено. | 1 |
| Все прочие случаи. | 0 |
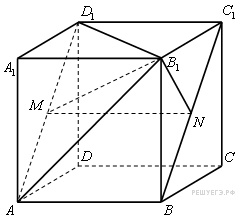
Дан куб 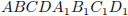 . Длина ребра куба равна 1. Найдите расстояние от середины отрезка
. Длина ребра куба равна 1. Найдите расстояние от середины отрезка 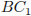 до плоскости
до плоскости  .
.
|
|
|
Решение.
М — середина  , N — середина
, N — середина 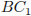 . Проведем перпендикуляр NH из точки N к плоскости
. Проведем перпендикуляр NH из точки N к плоскости  ,
, 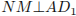 . Значит,
. Значит, 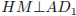 . Поэтому точка Н лежит на отрезке
. Поэтому точка Н лежит на отрезке 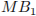 , перпендикулярном
, перпендикулярном  .
.
 Искомый отрезок NH является высотой прямоугольного треугольника
Искомый отрезок NH является высотой прямоугольного треугольника 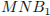 с прямым углом N.
с прямым углом N.
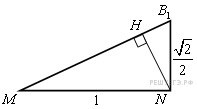
Поэтому 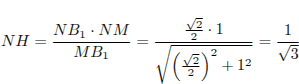 .
.
Ответ: 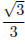 .
.
Задание С3 № 484592
| Критерии оценивания выполнения задания | Баллы |
| 3 | |
| 2 | |
| 1 | |
| 0 | |
| Максимальный балл | 3 |
Решите неравенство 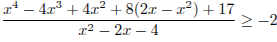 .
.
Решение.
Выполним преобразования:
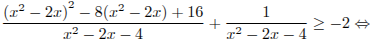
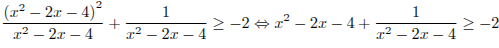 .
.
Сделаем замену: 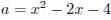 .
.
Получим:  , откуда
, откуда 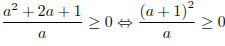 .
.
Решая это неравенство, находим:  или
или 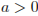 .
.
Если 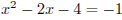 , то
, то 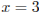 или
или 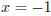 .
.
Если 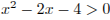 , то
, то 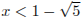 или
или  .
.
Ответ: 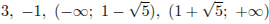 .
.
Задание С4 № 484626
| Содержание критериев оценивания задачи С4 | Баллы |
| Обоснованно получен верный ответ. | 3 |
| Рассмотрены все возможные геометрические конфигурации. В одном из случаев обоснованно получен верный ответ. | 2 |
| Рассмотрены только одна из возможных геометрических конфигураций. Для нее обоснованно получен верный ответ. | 1 |
| Все прочие случаи. | 0 |
Дана окружность радиуса 4 с центром в точке О, расположенной на биссектрисе угла, равного 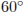 . Найдите радиус окружности, вписанной в данный угол и касающейся данной окружности внешним образом, если известно, что расстояние от точки О до вершины угла равно 10.
. Найдите радиус окружности, вписанной в данный угол и касающейся данной окружности внешним образом, если известно, что расстояние от точки О до вершины угла равно 10.
|
|
|
Решение.
Пусть Q — центр искомой окружности радиуса х, М — точка касания с данной окружностью, В — точка касания с одной из сторон данного угла с вершиной А. Центр окружности, вписанной в угол, лежит на биссектрисе угла, поэтому  . Из прямоугольного треугольника BAQ находим, что
. Из прямоугольного треугольника BAQ находим, что 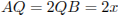 . Пусть точка Q лежит между А и О (рис. 1).
. Пусть точка Q лежит между А и О (рис. 1).

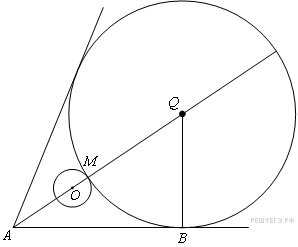 Линия центров касающихся окружностей проходит через точку их касания, поэтому
Линия центров касающихся окружностей проходит через точку их касания, поэтому  , или
, или 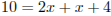 , откуда находим, что
, откуда находим, что  .
.
Пусть точка О лежит между А и Q (рис. 2),
тогда 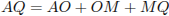 , или
, или 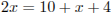 , откуда
, откуда 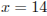 .
.
Ответ: 2 или 14.
Задание С5 № 484627
| Содержание критериев оценивания задачи С5 | Баллы |
| Обоснованно получен верный ответ. | 4 |
| Рассмотрены все возможные случаи. Получен верный ответ, но решение либо содержит пробелы, либо вычислительную ошибку или описку. | 3 |
| Рассмотрены все возможные случаи. Получен ответ, но решение содержит ошибки. | 2 |
| Рассмотрены некоторые случаи. Для рассмотренных случаев получен ответ, возможно неверный из-за ошибок. | 1 |
| Все прочие случаи. | 0 |
Найдите все значения а, при каждом из которых система  не имеет решений.
не имеет решений.
Решение.
Рассмотрим второе неравенство системы 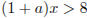 .
.
Если  , то неравенство, а значит, и система не имеет решений. Если
, то неравенство, а значит, и система не имеет решений. Если  , то решение неравенства — луч
, то решение неравенства — луч  .
.
Если 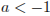 , то решение неравенства — луч
, то решение неравенства — луч 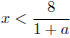 .
.
При 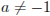 первое неравенство системы принимает вид
первое неравенство системы принимает вид

Если  , то решение этой системы — два луча с концами в точках
, то решение этой системы — два луча с концами в точках  . Если
. Если 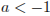 , то решение этой системы — полуинтервал с концами в точках
, то решение этой системы — полуинтервал с концами в точках 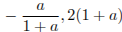 .
.
Отметим, что точки 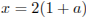 нет во множестве решений второго неравенства. Для того, чтобы система не имела решений, при
нет во множестве решений второго неравенства. Для того, чтобы система не имела решений, при 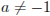 необходимо и достаточно:
необходимо и достаточно:
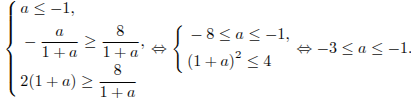
Ответ: 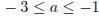 .
.
Задание С6 № 484663
| Критерии оценивания выполнения задания | Баллы |
| 4 | |
| 3 | |
| 2 | |
| 1 | |
| 0 | |
| Максимальный балл | 4 |
Найдите все простые числа p, для каждого из которых существует такое целое число k, что число p является общим делителем чисел 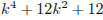 и
и 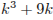 .
.
Решение.
Если число p является делителем числа 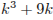 , то оно является также и делителем числа
, то оно является также и делителем числа 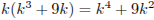 . Но если число p является общим делителем чисел
. Но если число p является общим делителем чисел 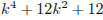 и
и 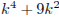 , то оно является также и делителем разности этих чисел, то есть числа
, то оно является также и делителем разности этих чисел, то есть числа
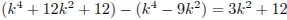 .
.
Аналогично получаем:
1) число p является общим делителем чисел 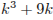 и
и 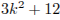 , значит, p является делителем числа
, значит, p является делителем числа
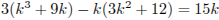 ;
;
2) число p является общим делителем чисел 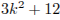 и
и 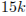 , значит, p является делителем числа
, значит, p является делителем числа
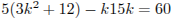 ;
;
Число 60 имеет ровно три различных простых делителя — 2, 3 и 5. Остается проверить найдутся ли такие целые числа k для каждого из которых одно из чисел 2, 3 и 5 является общим делителем чисел 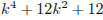 и
и 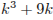 .
.
Если число k — четное, то число 2 является общим делителем данных чисел. Если число k кратно 3, то число 3 является общим делителем данных чисел. Если число 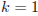 , то число 5 является общим делителем данных чисел.
, то число 5 является общим делителем данных чисел.
Ответ: 2, 3, 5.
Дата добавления: 2018-06-27; просмотров: 243; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
