Свойства симметричного тензора второго ранга
Усимметричного тензора второго ранга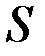 
из девяти компонент независимыми являются
только шесть. Вектор 
можно представить плоскостью
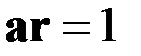. (73)
Здесь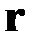 
-радиус-вектор точки плоскости. Это уравнение определяет плоскость, перпендикулярную к вектору и отстоящую от начала координат на расстояние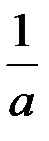 
. На прямой, проходящей через начало координат и имеющей направление 
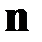, плоскость отсекает отрезок длины
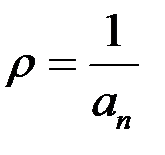. (74)
Плоскость является геометрическим образом вектора, длина которого равна обратной величине расстояния от начала отсчета до данной плоскости, а направление совпадает с нормалью к плоскости, направленной из начала отсчета.
Рассмотрим уравнение
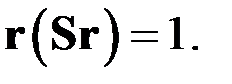(75)
В произвольной системе координат имеем
Следовательно, уравнение (75) имеет вид
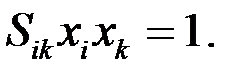(76)
Подробно
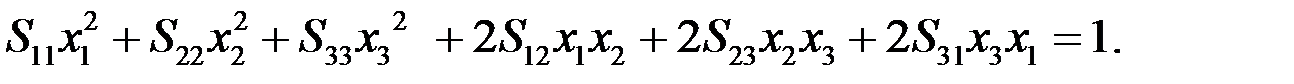(77)
Уравнение (77) есть уравнение поверхности второго порядка, центр которой помещается в начале координат. В физических задачах диагональные компоненты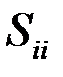 
обычно больше 0. В этом случае поверхность (77) представляет собой эллипсоид.
Этот эллипсоид и является геометрическим образом симметричного тензора второго ранга. Уравнение (77) называется уравнением тензорного эллипсоида.
Найдем расстояние от центра эллипсоида до точек, лежащих на его поверхности. Для этого проведем из центра эллипсоида произвольную прямую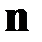 
, которую примем за ось 
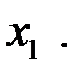Тогда расстояние 
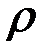от центра эллипсоида до точки Р будет равно значению 
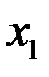при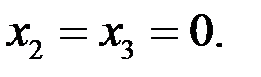 
Отсюда
|
|
|
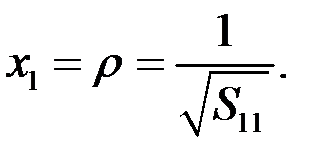
При преобразованиях координат изменяются коэффициенты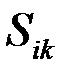 
, однако сам эллипсоид от выбора системы координат не зависит. Если направить оси координат вдоль полуосей эллипсоида, уравнение эллипсоида принимает вид
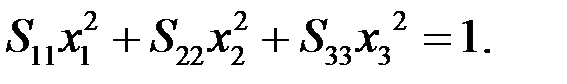
Главные оси тензора совпадают с полуосями тензорного эллипсоида. Если координатные оси направить вдоль полуосей эллипсоида, тензор принимает диагональный вид
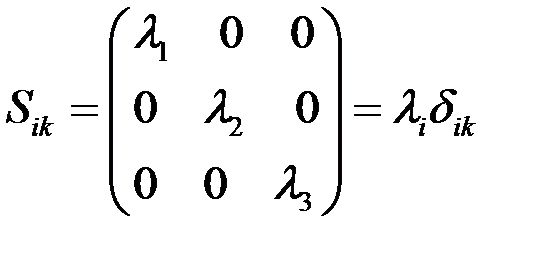. (78)
В (78) нет суммирования по повторяющемуся индексу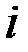 
.
Величины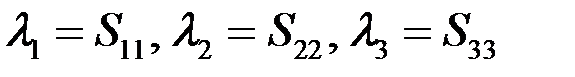 
- главные значения тензора. В случае, когда
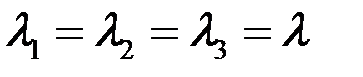тензорный эллипсоид превращается в сферу. В частности, единичному тензору 
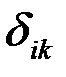соответствует сфера единичного радиуса.
Умножим вектор на тензор (78). В результате получим
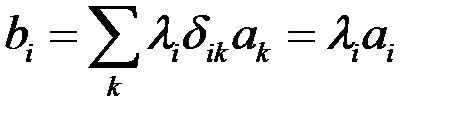. (79)
Здесь нет суммирования по повторяющемуся индексу 
.Пусть вектор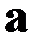 
направлен вдоль первой главной оси тензора. Тогда
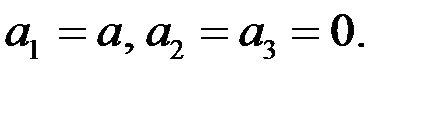
При этом из формулы (69)
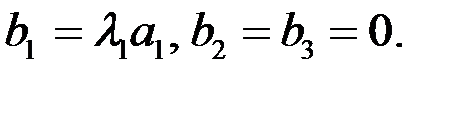
Для других осей аналогично. Таким образом, если вектор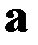 
направлен по одной из главных осей тензора, то справедливо следующее равенство:
|
|
|
(80)
Здесь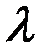 
- соответствующее главное значение тензора. Запишем равенство (70) в компонентах. Будем предполагать, что тензор пока не приведен к главным осям. Имеем
,
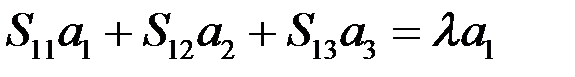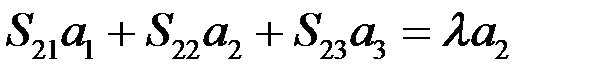, (81)
.
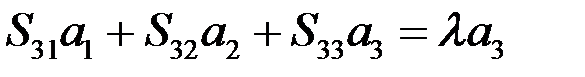Для существования нетривиального решения должно выполняться
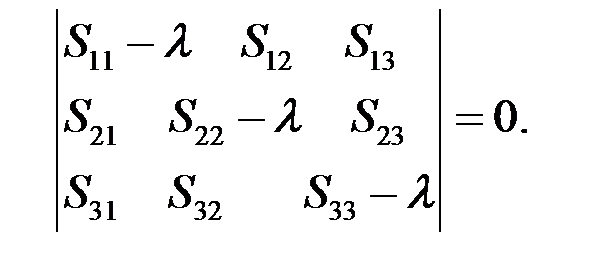(82)
Корни этого кубического уравнения представляют собой главные значения тензора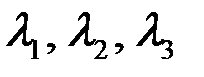 
. Подставив один из корней в систему (81), определим 
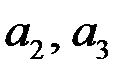при заданном 
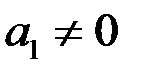, которые определят направление вектора 
, т.е. соответствующую главную ось тензора. Проделав эту операцию для всех трех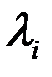 
, найдем направления всех главных осей. Мы предполагали, что все корни 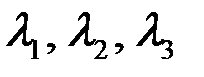различны. При двух кратных корнях тензорный эллипсоид будет эллипсоидом вращения. Однозначно будет определена только одна главная ось тензора, совпадающая с осью симметрии эллипсоида. В качестве двух других главных осей можно взять две любые взаимно-перпендикулярные оси, перпендикулярные к оси симметрии эллипсоида.
Дата добавления: 2018-06-27; просмотров: 643; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!