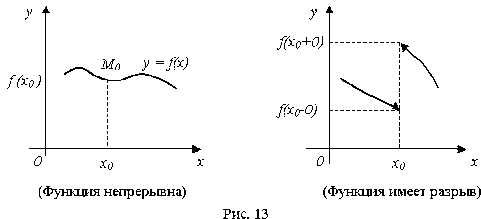Бесконечно – малые и бесконечно – большие функции и их связь



Непрерывность функции, точки разрыва. Основные теоремы о непрерывных функциях
| Непрерывность функции, точки разрыва | |
|

Производная. Производная сложной функции. Производные высших порядков
Производная функция - базовый элемент дифференциального исчисления, который является результатом применения какой-либо операции дифференцирования к исходной функции.

Название функции происходит от слова «произведенная», т.е. образованная от другой величины. Процесс определения производной какой-либо функции называется дифференцированием. Распространенный способ представления и определения - через теорию пределов, хотя она возникла позже дифференциального исчисления. Согласно этой теории производная - это предел отношения приращения функции к приращению аргумента, если такой предел существует, при условии, что аргумент стремится к нулю. Считается, что впервые термин «производная» употребил известный русский математик В.И.Висковатов.Чтобы найти производную функции f в точке x, необходимо определить значения этой функции в точке х и в точке x+ x, где x – приращение аргумента х. Найти приращение функции y = f(x+ x) – f(x). Записать производную через предел отношения f’ = lim(f(x+ x) – f(x))/ x, вычислить при x 0. Принято обозначать производную знаком апостроф «’» над дифференцируемой функцией. Один апостроф – первая производная, два – вторая, производная высшего порядка задается соответствующей цифрой, например, f^(n) – производная n-го порядка, где n – целое число 0.
|
|
|

Производные высших порядков
Пусть функция y = f(x) имеет производную y' = f'(x) во всех точках некоторой окрестности точки x0. Если функция f'(x) в свою очередь имеет в точке x0 производную 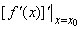 , то она называется второй производной функции f в точке x0 и обозначается f"(x0) или f(2)(x0). Таким образом, опуская обозначения аргумента, имеем
, то она называется второй производной функции f в точке x0 и обозначается f"(x0) или f(2)(x0). Таким образом, опуская обозначения аргумента, имеем
y(2) 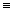 y"
y"  (y')'.
(y')'.
Аналогично определяются и производные y(n) более высоких порядков n:
| y(n+1) = [y(n)]', n = 0, 1, 2, ..., |
где для удобства считается, что y(0) = y.
Примеры.
1. Если y = ax, a > 0, то y' = ax ln a, y" = ax ln2 a, вообще, y(n) = ax lnn a, n = 0, 1, 2, ... В частности, если y = ex, то
|
|
|
| (ex)(n) = ex. |
2. Если y = sin x, y' = cos x, y(2) = -sin x, y(3) = -cos x, y(4) = sin x. Заметив, что cos x = sin (x +  /2), получим
/2), получим
y' = sin(x +  /2), y(2) = cos (x +
/2), y(2) = cos (x +  /2) = sin(x + 2
/2) = sin(x + 2  /2).
/2).
Вообще,
sin(x)(n) = sin(x + n  /2). /2).
|
Аналогично,
cos(x)(n) = cos(x + n  /2), n = 0, 1, 2, .. /2), n = 0, 1, 2, ..
|
Дата добавления: 2018-05-13; просмотров: 622; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 непрерывна в точке
непрерывна в точке  , если
, если
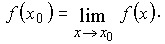 Графически же непрерывность функции y = f(x) означает непрерывность ее графика как линии на плоскости Oxy.
Имеет место следующая теорема (критерий непрерывности).
Теорема. Функция f(x),
Графически же непрерывность функции y = f(x) означает непрерывность ее графика как линии на плоскости Oxy.
Имеет место следующая теорема (критерий непрерывности).
Теорема. Функция f(x), 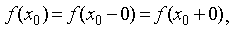
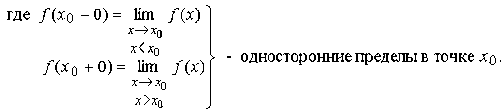 Как видно из рис. 13, в точке x0 разрыва функции f(x) ее левая "половина графика" не соединяется с "правой половиной", т.е. график "разорвался", а поэтому f(x) в точке x0 имеет разрыв.
Как видно из рис. 13, в точке x0 разрыва функции f(x) ее левая "половина графика" не соединяется с "правой половиной", т.е. график "разорвался", а поэтому f(x) в точке x0 имеет разрыв.