Метод математической индукции
Пусть мы имеем бесконечную последовательность утверждений P1, P2, ...,
Pn, ..., занумерованных натуральными числами, причём:
— утверждение P1 истинно;
— если некоторое утверждение Pk истинно, то следующее утверждение Pk+1
тоже истинно.
Тогда принцип математической индукции утверждает, что все утверждения
последовательности истинны.
Другими словами принцип математической индукции можно
сформулировать так: если в очереди первой стоит женщина, и за каждой
женщиной стоит женщина, то все в очереди – женщины.
Способ рассуждений, основанный на принципе математической индукции
называется методом математической индукции. Для решения задач методом
математической индукции необходимо:
1) сформулировать утверждение задачи в виде последовательности
утверждений P1, P2, ..., Pn, ...
2) доказать, что утверждение P1 истинно (этот этап называется базой
индукции); 3) доказать, что если утверждение Pn истинно при некотором n
= k, то оно истинно и при n = k + 1 (этот этап называется шагом
индукции).
Функция
Функция— математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).
Свойства: область определения; область значения; четность; возрастание, убывание; периодичность.
|
|
|
Четность
Функция f (x) называется четной, если для любого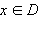 
выполняются равенства:
1) 
,
2) f (–x) = f (x).
График четной функции на всей области определения симметричен относительно оси OY. Примерами четных функций могут служить y = cos x, y = |x|, y = x2 + |x|.
Функция f (x) называется нечетной, если для любого 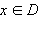выполняются равенства:
1) ,
2) f (–x) = –f (x).
Иными словами функция называется нечетной, если ее график на всей области определения симметричен относительно начала координат. Примерами нечетных функций являются y = sin x, y = x3.
Монотонность
Функция f (x) называется возрастающей на промежутке D, если для любых чисел x1 и x2 из промежутка D таких, что x1 < x2, выполняется неравенство f (x1) < f (x2).
Функция f (x) называется убывающей на промежутке D, если для любых чисел x1 и x2 из промежутка D таких, что x1 < x2, выполняется неравенство f (x1) > f (x2).
Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке.
Ограниченность функций
Если для любого (xÎD, x ≠ a) выполняется неравенство f (x) ≤ f (a) , aÎD то точка a называется точкой наибольшего значения функции на множестве D:
|
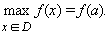
Если для любого xÎD выполняется неравенство f (x) > f (b) bÎD то точка b называется точкой наименьшего значения функции на множестве D.
|
|
|
|
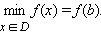
Если существует число C такое, что для любого xÎD выполняется неравенство f (x) ≤ C, то функция f называется ограниченной сверху на множестве D.
Если существует число c такое, что для любого xÎD выполняется неравенство f (x) ≥ c, то функция f называется ограниченной снизу на множестве D.
Функция, ограниченная и сверху, и снизу, называется ограниченной на множестве D. Геометрически ограниченность функции f на множестве D означает, что график функции y = f (x), xÎD лежит в полосе c ≤ y ≤ C.
Если функция не является ограниченной на множестве, то говорят, что она не ограничена.
Примером функции, ограниченной снизу на всей числовой оси, является функция y = x2.
Примером функции, ограниченной сверху на множестве (–∞; 0) является
функция y = 
.
Примером функции, ограниченной на всей числовой оси, является функция y = sin x.
Дата добавления: 2018-05-13; просмотров: 239; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!