Основные методы решения тригонометрических неравенств

К простейшим тригонометрическим неравенствам относятся неравенства:

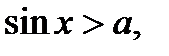
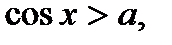
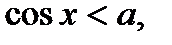
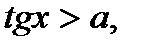
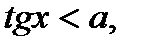
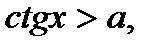
(1)

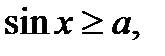
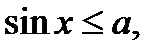
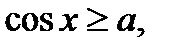
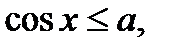
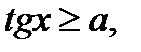
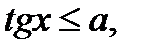
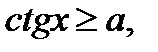
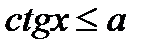(2)

Для решения таких неравенств можно использовать, в частности, единичную окружность (рис. 1 – 4). Строят «граничные углы», соответствующие равенству в заданном неравенстве (т.е. в случае замены знаков неравенства на знак равенства). Исходя из смысла неравенства определяют множество углов, которые являются решением (если такие имеются). Для строгих неравенств (1) (соотв . рис. 1 – 4) решения приведены в таблице.

Решение простейших тригонометрических неравенств.С помощью единичной окружности нетрудно получить множества решений простейших тригонометрических неравенств.

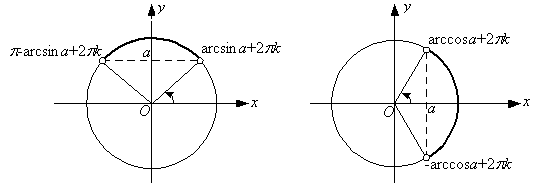
Рис.1 Рис. 2

Неравенства	Множества решений неравенств (kÎZ)


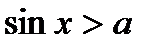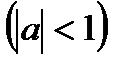
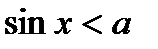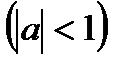
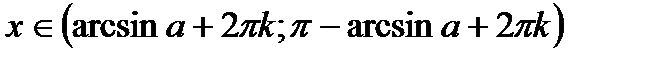
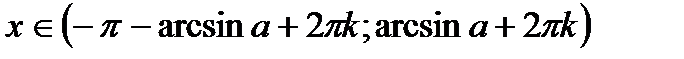
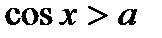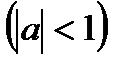
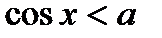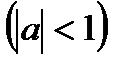
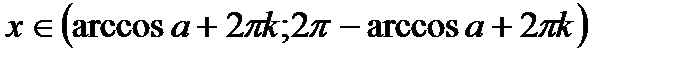
tgx > a tgx < a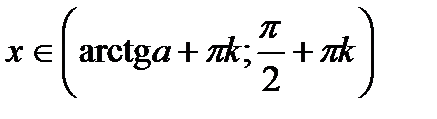

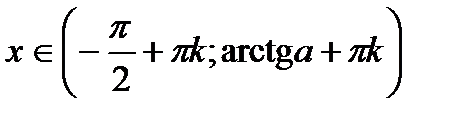
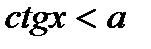
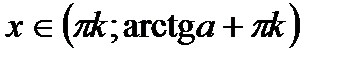
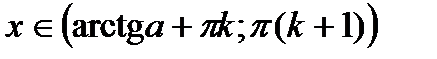
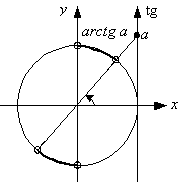
Рис. 3

Более сложные тригонометр. неравенства решаются сведением к простейшим (если это возможно).

Если решают нестрогие неравенства, то в соответствующие промежутки, указанные во множестве решений (см. таблицу) включают граничные точки. При этом следует учитывать, что для неравенств, содержащих 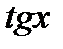и 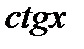не включаются концы промежутка, которые не входят в ОДЗ этих функций. Если задано тригонометрическое неравенство, которое не является простейшим, то его решают вначале в зависимости от типа (в частности, разложением на множители, заменой переменной), а затем решают полученные простейшие неравенства.

Метод интервалов при решении тригонометрических неравенств

Пример. Решить неравенство .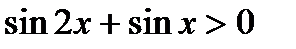

Решение. Рассмотрим функцию 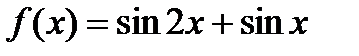. Она определена и непрерывна на множестве всех действительных чисел. Функци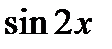и и 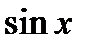имеют периоды 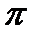и 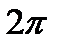соответственно. Следовательно, период 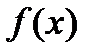равен 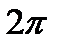. Найдем нули функции:

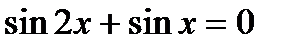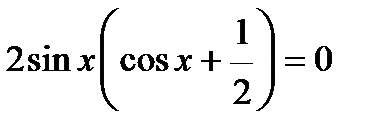; , откуда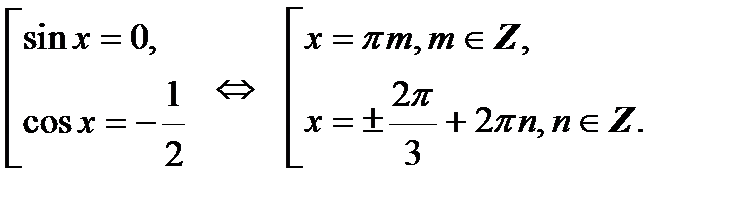

Выберем промежуток , длина которого равна периоду 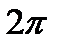. Нетрудно заметить, что его концы являются нулями функции (можно было выбрать любой промежуток длины 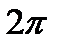, но сделанный выбор позволит записать ответ в более компактном виде).

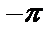
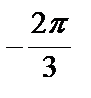
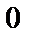
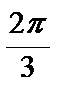
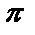
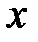
Найдем решения исходного неравенства на выбранном интервале. Для этого отметим на промежутке нули функции и определим знак 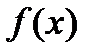на каждом из получившихся интервалов. Функция 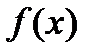принимает положительные значения на интервалах .

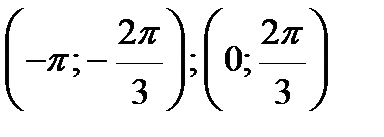Ответ:

Доказательство тригонометрических неравенств

При доказательстве тригонометрических неравенств применяют те же методы, что и при доказательстве алгебраических неравенств (вопросы 18,19). Однако, если в процессе доказательства тригонометрических неравенств используется синтетический метод, то в качестве опорных часто берутся следующие неравенства:

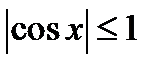, , , где 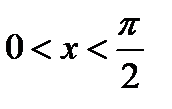. Иногда в качестве опорных используют неравенства, вытекающие из монотонности тригонометрических функций. Так, в интервале 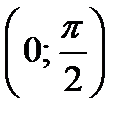функци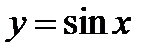и и 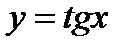возрастают, а функци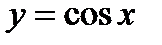и и 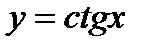убывают. Поэтому если , то , , 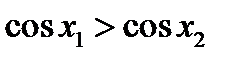, 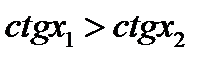. Аналогичные неравенства можно получить и для других промежутков монотонности тригонометрических функций.