Понятие определённого интеграла
Определение:Если F(x)+C первообразная функции f(x), то приращение F(b)-F(a) первообразной функции при изменении аргумента х от х=а до х=b называется определённым интегралом и обозначается символом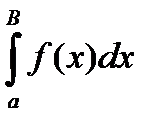 
, т,е
|
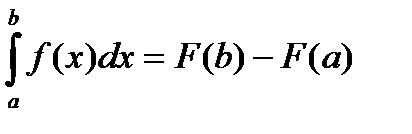
формула Ньютона-Лейбница
Интегрирование подстановкой
Теорема: Пусть функция f(t) непрерывна в любой точке t=j(x), где xÎ[a,b] и пусть a=j(a), b=j(b). Тогда если функция j(х) имеет непрерывную производную, то справедлива следующая формула.
|
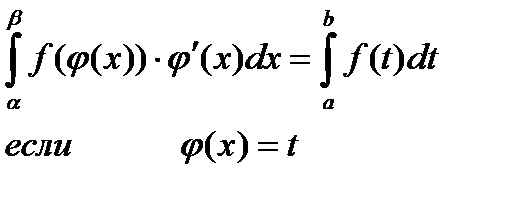
формула замены переменной в определённом интеграле
Для вычисления определённого интеграла способом подстановки поступают так же, как и при вычислении неопределённого интеграла этим способом. Однако нужно помнить одну особенность: в случае определённого интеграла нет необходимости возвращаться к первоначальной переменной, но нужно помнить, что заменяя переменную под знаком интеграла следует изменить и пределы интегрирования.
План интегрирования способом подстановки.
1. Определяют к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подынтегральное выражение, если нужно).
- Определяют, какую часть подынтегральной функции заменить новой переменной и записывают эту замену.
- Находят дифференциалы обеих частей записи и выражают дифференциал старой переменной (или выражение, содержащее этот дифференциал) через дифференциал новой переменной.
- Находят новые пределы интегрирования.
- Производят замену под интегралом.
- Находят полученный интеграл.
Правило 1:Если подынтегральная функция имеет вид f(ax+b), то может оказаться полезной подстановка t=ax+b.
|
|
|
Пример 1:
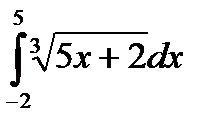
| Определяем к какому табличному интегралу приводится данный интеграл |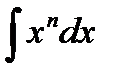 
|
| Определяем, какую часть подынтегральной функции заменить новой переменной и записываем эту замену. |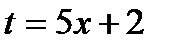 
|
| Находим дифференциалы обеих частей записи и выражаем дифференциал старой переменной через дифференциал новой переменной. |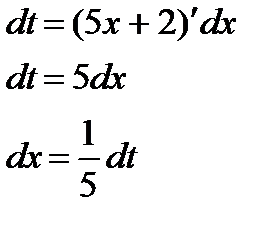 
|
| Находим новые пределы интегрирования | хнижнее= -2 tнижнее = 5×(-2)+2= -8 xверхнее= 5 tверхнее= 5×5+2=27 |
| Производим замену под интегралом | 
|
| Находим полученный интеграл. |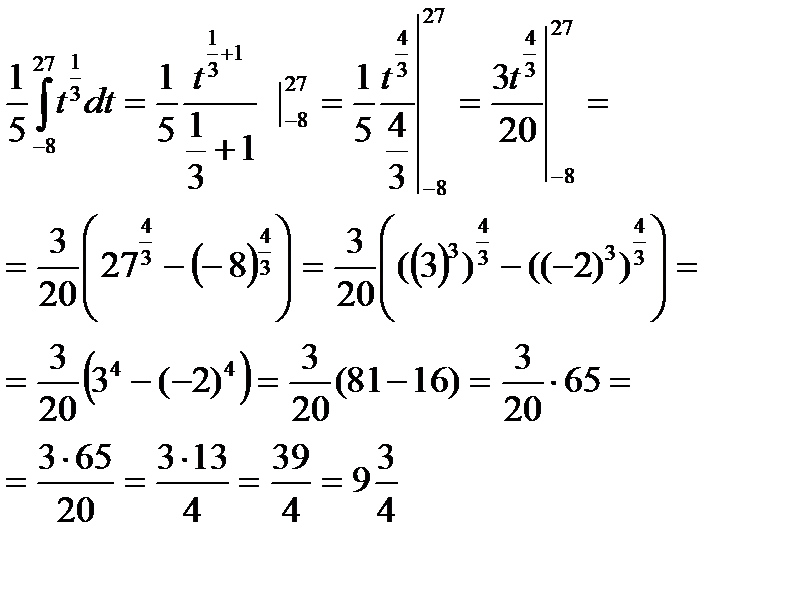 
|
Иногда перед тем как сделать подстановку подынтегральное выражение надо преобразовать.
Пример 2:
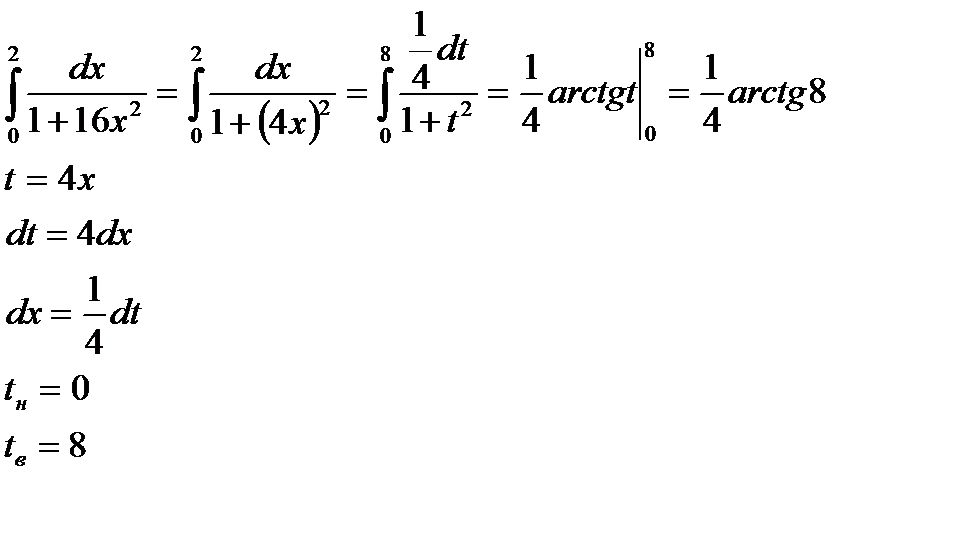
Правило 2:Пусть подынтегральное выражение разбито на два сомножителя и в одном из них легко распознать дифференциал функции j(х). Может оказаться, что после подстановки t=j(х) второй сомножитель превратиться в такую функцию от t, которую легко проинтегрировать. Тогда подстановка окажется полезной.
Пример 3:
Интегрирование по частям
Теорема:Если функции u(x) и v(x) имеют непрерывные производные на отрезке [a;b], то справедлива формула
|
|
|
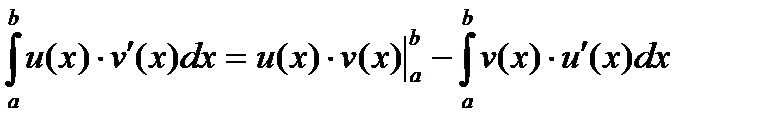
формула интегрирования по частям в определённом интеграле
|
При практическом использовании формулы интегрирования по частям данное подынтегральное выражение представляют в виде произведения двух сомножителей, которые обозначают u и dv. Множитель u выбирают так, чтобы u’ было проще, чем u.
Замечание 1:В интегралах вида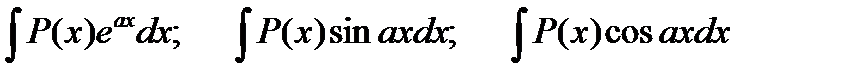 
, где Р(х) – многочлен относительно х, а - некоторое число. Полагают u=P(x), а все остальные сомножители за dv. Если Р(х) – многочлен степени выше первой, то операцию интегрирования по частям следует повторить несколько раз.
Пример 4.
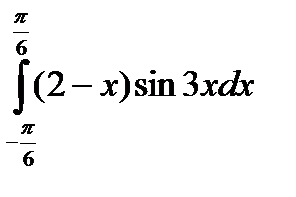
| Представим данное подынтегральное выражение в виде произведения двух сомножителей, которые обозначим u и dv. | u=2-x dv=sin3xdx |
| Зная u найдём du (du=u’dx) | du=-dx |
Зная dv найдём v (v=  )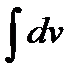
| 
|
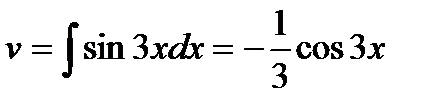
| Подставим всё в формулу интегрирования по частям ( )
| 
|
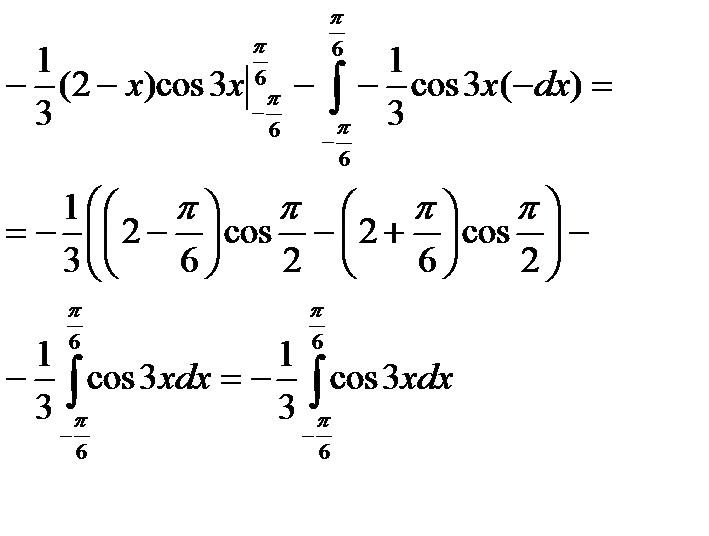
| Вычислим второй интеграл |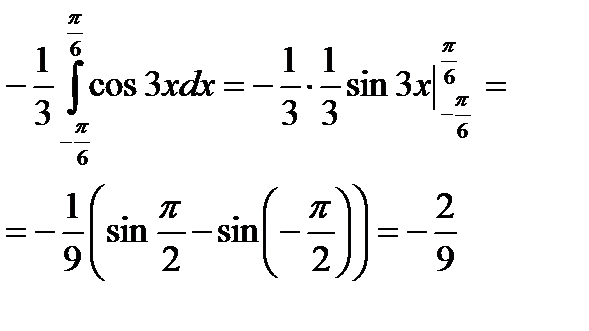 
|
Замечание 2:В интегралах вида 
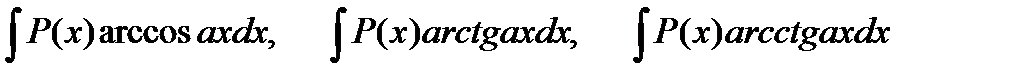полагают P(x)dx=dv, а остальные сомножители u.
Пример 5:
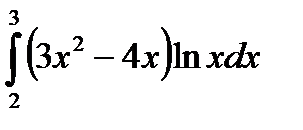
| Представим данное подынтегральное выражение в виде произведения двух сомножителей, которые обозначим u и dv. |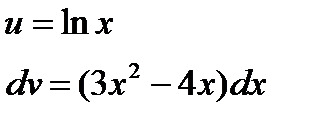 
|
| Зная u найдём du (du=u’dx) |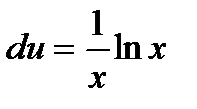 
|
| Зная dv найдём v (v= )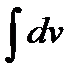
| 
|
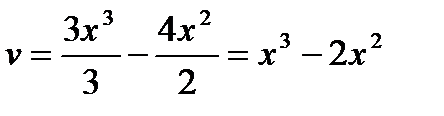
| Подставим всё в формулу интегрирования по частям ( )
|  
|
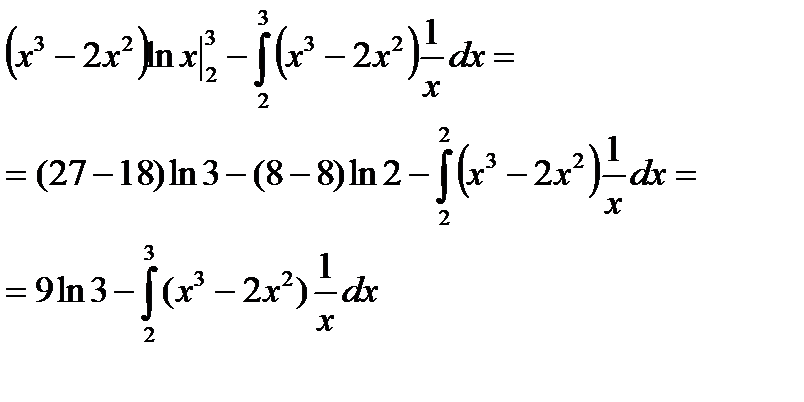
| Вычислим второй интеграл, предварительно раскрыв скобки в подынтегральном выражении |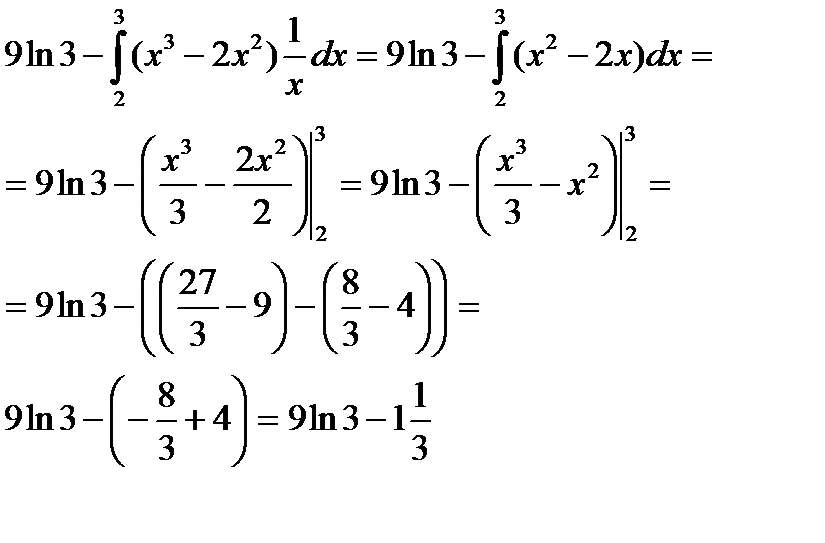 
|
|
|
|
Интегрирование рациональных функций
Интегрирование дробей типа 
(D=p2-4q>0, трёхчлен имеет действительные корни).
Пример 6:
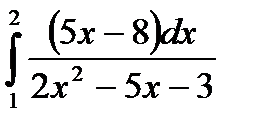
| Разложим квадратный трёхчлен на множители по формуле ax2+bx+c=a(x-x1)(x-x2), где х1 и х2 – корни трёхчлена. | 2х2-5х-3=2(х-3)(х+ 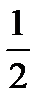 )=(х-3)(2х+1)
D=25-4×2×(-3)=49
|
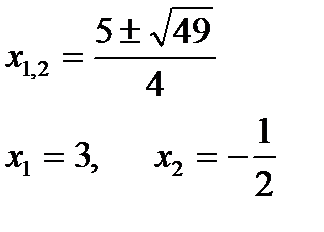
| Выпишем подынтегральное выражение и представим его в виде суммы двух дробей. | 
|
| Чтобы найти коэффициенты А и В приведём дроби к общему знаменателю |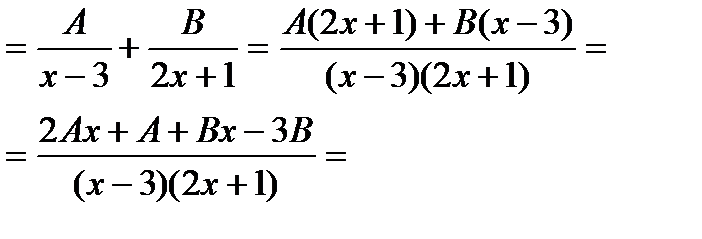 
|
| Выполним группировку в числителе |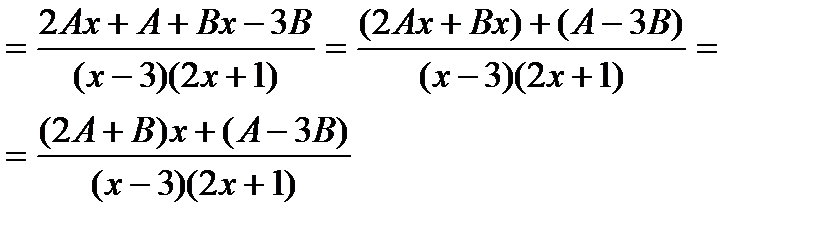 
|
| Получили равенство |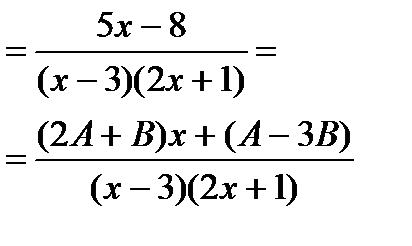 
|
| Две дроби с равными знаменателями равны, если равны их числители | 5х-8=(2А+В)х+(А-3В) |
| Два многочлена равны, если равны коэффициенты при одинаковых степенях переменной, поэтому получим систему |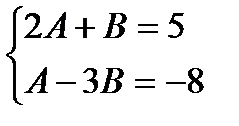 
|
| Решим эту систему методом подстановки. Выразим из первого уравнения В и подставим во второе | В=5-2А А-3(5-2А)=-8 |
| Решим полученное уравнение | А-15+6А=-8 7А=7 А=1 |
| Подставим полученное значение А в первое уравнение и найдём В | В=5-2×1=3 |
| Итак подынтегральное выражение можно представить в виде суммы двух дробей |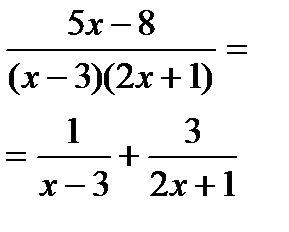 
|
| Подставим полученное выражение под знак интеграла |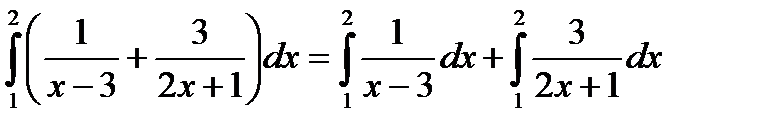 
|
| Для вычисления каждого интеграла сделаем подстановку |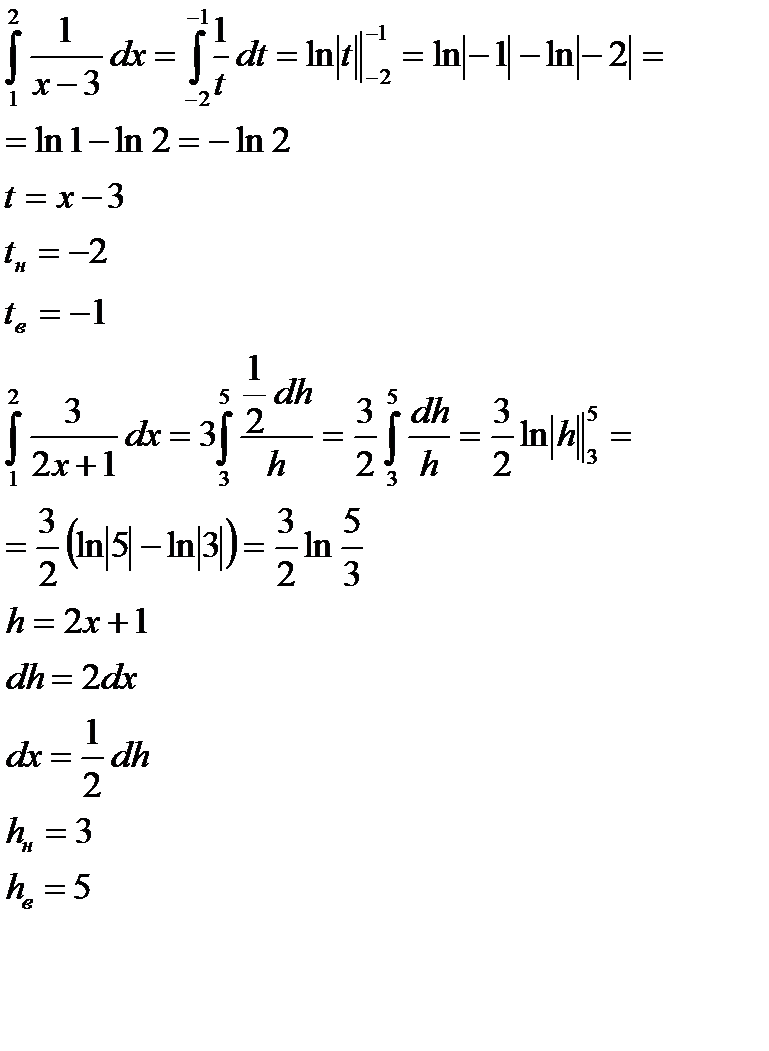  
|
| Окончательно получим |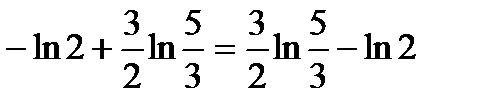 
|
Интегрирование дробей типа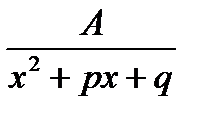 
(D=p2-4q<0, трёхчлен не имеет действительных корней).
|
|
|
Пример 7.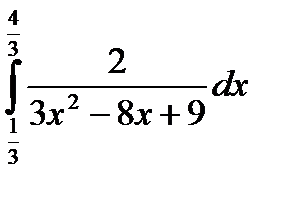 
| Выделим полный квадрат в знаменателе |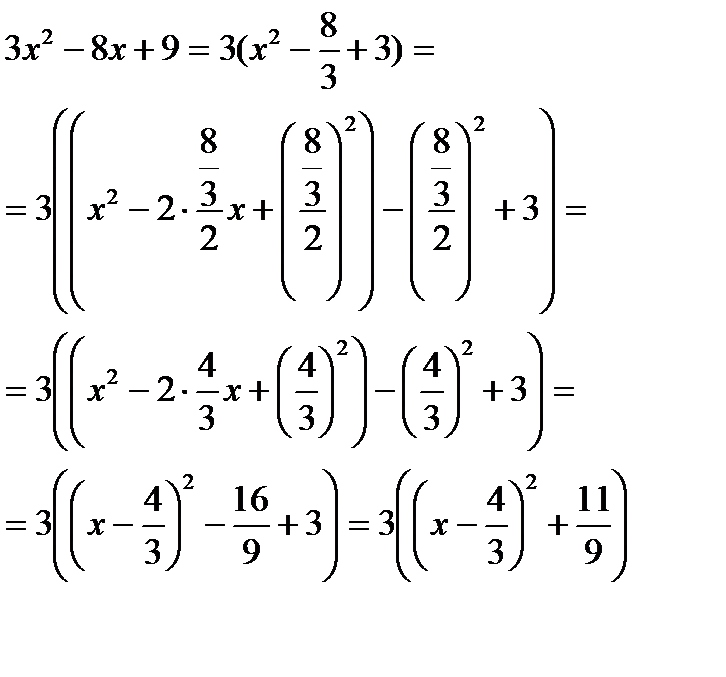 
|
| Запишем полученное выражение под знак интеграла |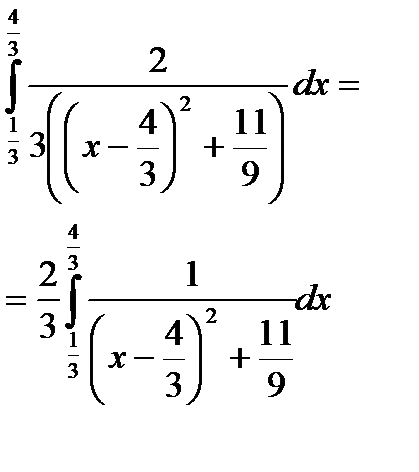 
|
| Выполним подстановку |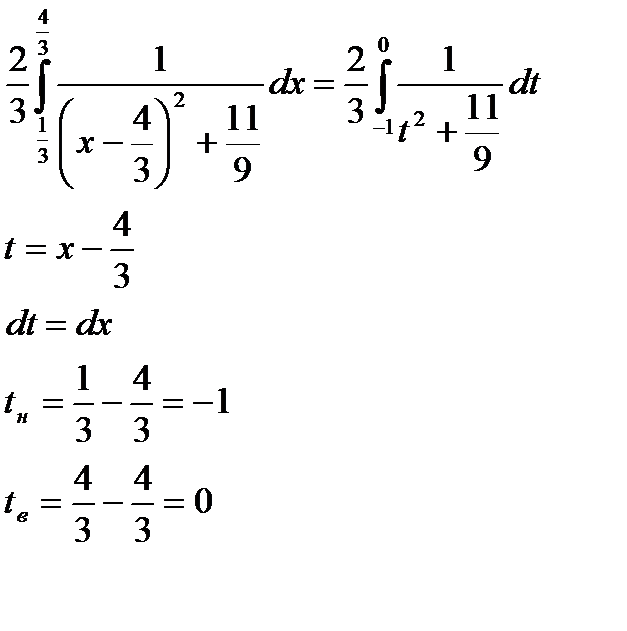 
|
| Найдём табличный интеграл |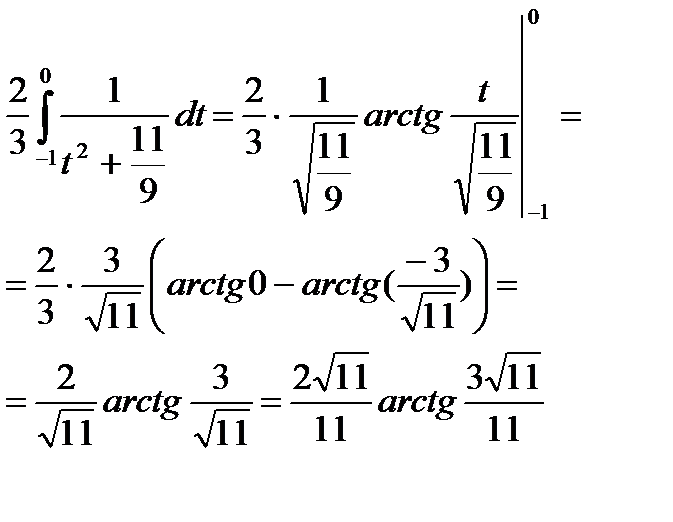 
|
Интегралы вида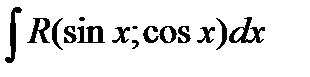 
Под знаком интеграла стоит рациональная функция от sinx и cosx. Она приводится к интегралу от рациональной функции подстановкой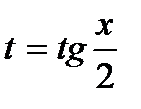 
(универсальная тригонометрическая подстановка). При этом
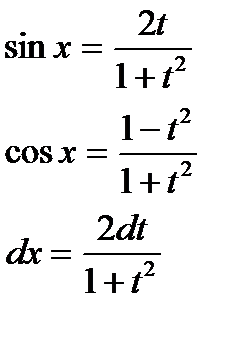
Пример 8:
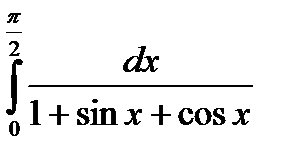
| Выполним подстановку | 
|
Дата добавления: 2018-05-12; просмотров: 305; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!