Логическая операция ИСКЛЮЧАЮЩАЯ ДИЗЪЮНКЦИЯ
(строгая дизъюнкция, исключающее или, сложение по модулю 2)
Логическая операция исключающая дизъюнкция(eXcluding OR, строгая дизъюнкция, исключающее или, сложение по модулю 2):
– в естественном языке соответствует союзу «либо»;
– в алгебре высказываний обозначается Å;
– в языках программирования обозначается xor.
Исключающая дизъюнкция – это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся истинным тогда и только тогда, когда истинно либо первое простое высказывание, либо второе, но не оба сразу.
Исключающей дизъюнкцией элементарных высказываний «Данное число четно», «Число больше данного на единицу, четно» будет составное высказывание «Данное число четно либо число больше данного на единицу, четно».
Исключающую дизъюнкцию можно выразить через конъюнкцию, дизъюнкцию и инверсию (17), (18):
| (17) |
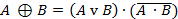 ,
,
| (18) |
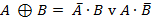 ,
,
Таблица истинности исключающей дизъюнкции приведена в таблице 9, диаграмма Эйлера-Венна – на рисунке 8.
Таблица 9 – Таблица истинности
исключающей дизъюнкции
| A | B | A Å B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| B |
| A |
| Рисунок 8 – Диаграмма Эйлера-Венна для исключающей дизъюнкции |

Логическая операция ИМПЛИКАЦИЯ (логическое следование)
Логическая операция импликация (от лат. «implico» – тесно связаны, логическое следование):
– в естественном языке соответствует оборотам «если ..., то ...», «... влечет ...», «из ... следует»;
|
|
|
– в алгебре высказываний обозначается ®.
Импликация – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.
Импликацией простых высказываний «Париж – столица Англии», «2х2=5» будет составное высказывание «Если Париж – столица Англии, то 2х2=5».
| (19) |

Таблица истинности импликации приведена в таблице 10, диаграмма Эйлера-Венна – на рисунке 9.
Таблица 10 – Таблица истинности импликации
| A | B | A ® B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| A |
| Рисунок 9 – Диаграмма Эйлера-Венна для импликации |
| B |
Логическая операция ЭКВИВАЛЕНЦИЯ
(равнозначность, равносильность, двойная импликация)
Логическая операцияэквиваленция:
– в естественном языке соответствует оборотам речи «тогда и только тогда», «в том и только в том случае»;
– в алгебре высказываний обозначается «, º, ~ ;
Эквиваленция(эквивалентность) – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.
|
|
|
Эквиваленцией двух простых высказываний «Число является четным», «Число делится без остатка на 2» будет составное высказывание «Число является четным тогда и только тогда, когда число делится без остатка на 2».
| (21) |
| (20) |
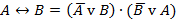
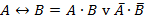
Таблица истинности эквиваленции приведена в таблице 11, диаграмма Эйлера-Венна – на рисунке 10.
Таблица 11 – Таблица истинности эквиваленции
| A | B | A « B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| Рисунок 10 – Диаграмма Эйлера-Венна для эквиваленции |
| B |
| A |
Порядок выполнения логических операций:
– действия в скобках,
– инверсия,
– конъюнкция,
– дизъюнкция,
– импликация, эквиваленция.
ЗАДАЧИ
1. Установите, какие из следующих предложений являются логическими высказываниями, а какие – нет (объясните почему):
а) «Солнце есть спутник Земли»;
б) «2+3?4»;
в) «сегодня отличная погода»;
г) «в романе Л.Н. Толстого «Война и мир» 3 432 536 слов»;
|
|
|
д) «Санкт-Петербург расположен на Неве»;
е) «музыка Баха слишком сложна»;
ж) «первая космическая скорость равна 7.8 км/сек»;
з) «железо — металл»;
и) «если один угол в треугольнике прямой, то треугольник будет тупоугольным»;
к) «если сумма квадратов двух сторон треугольника равна квадрату третьей, то он прямоугольный».
2. Укажите, какие из высказываний предыдущего задания истинны, какие – ложны, а какие относятся к числу тех, истинность которых трудно или невозможно установить.
3. Приведите примеры истинных и ложных высказываний:
а) из математики;
б) из физики;
в) из биологии;
г) из информатики;
д) из геометрии;
е) из жизни.
4. Сформулируйте отрицания следующих высказываний или высказывательных форм:
а) «Эльбрус – высочайшая горная вершина Европы»;
б) «2≥5»;
в) «10<7»;
г) «все натуральные числа целые»;
д) «через любые три точки на плоскости можно провести окружность»;
е) «теннисист Сафин не проиграл финальную игру»;
ж) «мишень поражена первым выстрелом»;
з) «это утро ясное и теплое»;
и) «число n делится на 2 или на 3»;
к) «этот треугольник равнобедренный и прямоугольный»;
л) «на контрольной работе каждый ученик писал своей ручкой».
5. Определите, какие из высказываний (высказывательных форм) в следующих парах являются отрицаниями друг друга, а какие нет:
|
|
|
а) «5<10», «5>10»;
б) «10>9», «10≤9»;
в) «мишень поражена первым выстрелом», «мишень поражена вторым выстрелом»;
г) «машина останавливалась у каждого из двух светофоров», «машина не останавливалась у каждого из двух светофоров»,
д) «человечеству известны все планеты Солнечной системы», «в Солнечной системе есть планеты, неизвестные человечеству»;
е) «существуют белые слоны», «все слоны серые»;
ж) «кит – млекопитающее», «кит – рыба»;
з) «неверно, что точка А не лежит на прямой а», «точка А лежит на прямой а»
и) «прямая а параллельна прямой b», «прямая a перпендикулярна прямой b»;
к) «этот треугольник равнобедренный и прямоугольный», «этот треугольник не равнобедренный или он не прямоугольный».
6. Определите значения истинности высказываний:
а) «наличия аттестата о среднем образовании достаточно для поступления в институт»;
б) «наличие аттестата о среднем образовании необходимо для поступления в институт»;
в) «если целое число делится на 6, то оно делится на 3»;
г) «подобие треугольников является необходимым условием их равенства»;
д) «подобие треугольников является необходимым и достаточным условием их равенства»;
е) «треугольники подобны только в случае их равенства»;
ж) «треугольники равны только в случае их подобия»;
з) «равенство треугольников является достаточным условием их подобия»;
и) «для того, чтобы треугольники были неравны, достаточно, чтобы они были неподобны»;
к) «для того, чтобы четырёхугольник был квадратом, достаточно, чтобы его диагонали были равны и перпендикулярны».
7. Подставьте в приведённые ниже высказывательные формы вместо логических переменных a, b, c, d такие высказывания, чтобы полученные таким образом составные высказывания имели смысл в повседневной жизни:
а) если (а или (b и с)), то d;
б) если (не а и не b), то (с или d);
в) (а или b) тогда и только тогда, когда (с и не d).
8. Формализуйте следующий вывод: «Если a и b истинны, то c – истинно. Но c – ложно: значит, a или b ложны».
9. Формализуйте предостережение, которое одна жительница древних Афин сделала своему сыну, собиравшемуся заняться политической деятельностью:
«Если ты будешь говорить правду, то тебя возненавидят люди.
Если ты будешь лгать, то тебя возненавидят боги.
Но ты должен говорить правду или лгать.
Значит, тебя возненавидят люди или возненавидят боги».
Формализуйте также ответ сына:
«Если я буду говорить правду, то боги будут любить меня.
Если я буду лгать, то люди будут любить меня.
Но я должен говорить правду или лгать.
Значит, меня будут любить боги или меня будут любить люди».
10. Пусть a = «это утро ясное», а b = «это утро теплое». Выразите следующие формулы на обычном языке:
1)  2)
2)  3)
3) 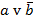 4)
4) 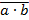 5)
5) 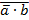 6)
6) 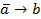
7) a 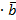 8)
8)  9)
9) 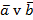 10)
10) 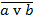 11) a
11) a  12)
12) 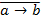
11. Из двух данных высказываний a и b постройте составное высказывание, которое было бы:
а) истинно тогда и только тогда, когда оба данных выказывания ложны;
б) ложно тогда и только тогда, когда оба данных высказывания истинны.
12. Из трех данных высказываний a, b, c постройте составное высказывание, которое истинно, когда истинно какое-либо одно из данных высказываний, и только в том случае.
Логические формулы
Высказывание можно формализовать – заменить логической формулой, состоящей из логических переменных и символов логических операций.
Логическая формула:
1. Элементарные формулы: любая логическая переменная и символы «1» («истина») и «0» («ложь») – формулы.
2. Правило образования новых формул: если А и В – формулы, то Ā, (А Ù В), (А v В), (А ® B) , (А«В) – формулы.
Других формул в алгебре логики нет.
В качестве примера рассмотрим высказывание «если я куплю яблоки или абрикосы, то приготовлю фруктовый пирог». Это высказывание формализуется в виде (A v B) ® C.
Такая же формула соответствует высказыванию «если Игорь знает английский или японский язык, то он получит место переводчика».
Как показывает анализ формулы (A v B) ® C, при определённых сочетаниях значений переменных A, Bи Cона принимает значение «истина», а при некоторых других – «ложь». Такие формулы называются выполнимыми.
Некоторые формулы принимают значение «истина» при любых значениях входящих в них переменных. Таковой будет, например, формула А v Ā, соответствующая высказыванию «Этот треугольник прямоугольный или косоугольный».
Эта формула истинна, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный. Такие формулы называются тождественно истиннымиили тавтологиями.
Высказывания, которые формализуются тавтологиями, называются логически истинными.
Высказыванию «Катя самая высокая девочка в классе, и в классе есть девочки выше Кати» соответствует формула А Ù Ā. Очевидно, формула будет ложной, так как либо значение А,либо Ā обязательно ложно. Такие формулы называются тождественно ложнымиили противоречиями. Высказывания, которые формализуются противоречиями, называются логическиложными.
Если две формулы А и В при одинаковых наборах значений, входящих в них переменных, принимают одинаковые значения, то они называются равносильными.
Равносильность двух формул алгебры логики обозначается символом «=» или символом «º». Замена формулы другой, равносильной ей, называется равносильным преобразованиемданной формулы.
Упрощение логических формул
Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определённому виду с использованием основных законов алгебры логики.
Под упрощением формулы, не содержащей операций импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая
1. содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции либо меньшее число вхождений переменных;
2. не содержит отрицаний неэлементарных формул.
Основные законы алгебры логики приведены в таблице 12.
Таблица 12 – Основные законы алгебры логики
| Закон | Для ИЛИ | Для И |
| Коммутативный (переместительный) | 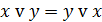
| 
|
| Ассоциативный (сочетательный) | 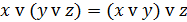
| 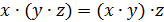
|
| Дистрибутивный (распределительный) | 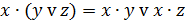
| 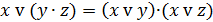
|
| Правила де Моргана | 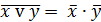
| 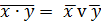
|
| Идемпотенции | 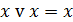
| 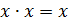
|
| Поглощения | 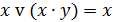
| 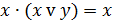
|
| Закон Порецкого | 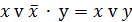
| 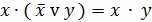
|
| Склеивания | 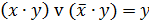
| 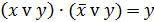
|
| Операция переменной с ее инверсией | 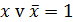
| 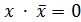
|
| Операция с константами | 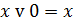 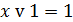
| 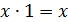
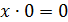
|
| Двойного отрицания |
| |
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре: вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п. Другие – основаны на свойствах, которыми не обладают операции обычной алгебры: использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.
Покажем на примерах некоторые приемы и способы, применяемые при упрощении логических формул.
Пример 4.4.1 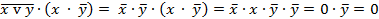 ,
,
применялись следующие законы алгебры логики: правило де Моргана для дизъюнкции, сочетательный закон, правило операций переменной с её инверсией, правило операций с константами.
Пример 4.4.2 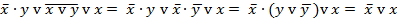 ,
,
использовали правило де Моргана для дизъюнкции, вынесли за скобки общий множитель, использовали правило операций переменной с её инверсией.
Пример 4.4.3 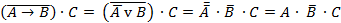 ,
,
выражаем импликацию через дизъюнкцию и инверсию, применяем правило де Моргана для дизъюнкции, применяем закон двойного отрицания.
При упрощении логических формул не всегда очевидно, какой из законов алгебры логики следует применить на том или ином этапе. Навыки приходят с опытом.
Пример 4.4.4Для какого из указанных значений числа X истинно выражение
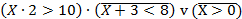 ?
?
1) 1 2) 2 3) 4 4) 7
Решение:преобразуем выражение таким образом, чтобы левая часть каждого неравенства содержала только X. Получим:
 .
.
Выполним инверсию:
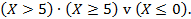
Выполним конъюнкцию:
 ,
,
Она будет истинной только в том случае, когдаоба неравенства примут значение«истина», т.е. при 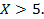
Рассмотрим дизъюнкцию:
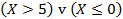 .
.
Дизъюнкция истинна только в том случае, когда истинно хотя бы одно из входящих в нее высказываний. Высказывание 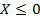 при данных вариантах ответа истинным быть не может. Следовательно, ищем такое значение X, при котором будет истинно первое высказывание
при данных вариантах ответа истинным быть не может. Следовательно, ищем такое значение X, при котором будет истинно первое высказывание  . Такое значение 7. Правильный ответ – 4.
. Такое значение 7. Правильный ответ – 4.
Пример 4.4.5Чему равно наименьшее целое значение числа X, при котором истинно выражение
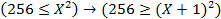 .
.
Преобразуем выражение, используя формулу (19):
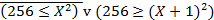 .
.
Инверсией выражения 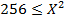 будет
будет 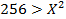 .
.
Отсюда:
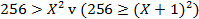
Для того чтобы дизъюнкция была истинной, должно быть истинным хотя бы одно из выражений.
Первое неравенство будет истинным при 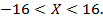 Второе при
Второе при 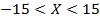 . Ответ: –16.
. Ответ: –16.
Пример 4.4.6Какое из перечисленных выражений является тождественно-ложным:
1) 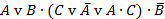 2)
2) 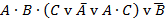
3) 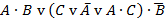 4)
4) 
Решение. Упростим логические выражения:
1) 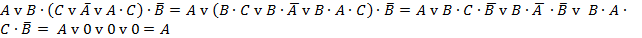 – формула не является тождественно-ложной;
– формула не является тождественно-ложной;
2) 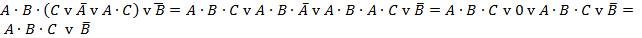 – формула не является тождественно ложной;
– формула не является тождественно ложной;
3) 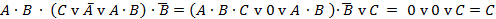 – формула не является тождественно-ложной;
– формула не является тождественно-ложной;
4) 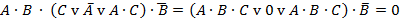 – формула является тождественно-ложной.
– формула является тождественно-ложной.
Ответ: 4.
Пример 4.4.7Какое из приведенных имен удовлетворяет логическому условию
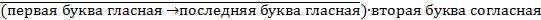
1) Ирина 2) Олег 3) Степан 4) Илона
Решение:введем условные обозначения. Пусть
А – первая буква гласная;
B – последняя буква гласная;
С – вторая буква согласная.
Тогда
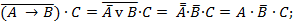
Это значит, что значения логических переменных А и С должно быть истинно, а значение В – ложно.
Проверяем ответы:
1) Ирина.
Первая буква гласная – 1;
Последняя буква гласная – 1;
Вторая буква согласная – 1.
Следовательно: 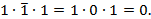 Ответ неверный.
Ответ неверный.
2) Олег.
Первая буква гласная – 1;
Последняя буква согласная – 0;
Вторая буква согласная – 1.
Следовательно: 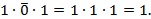 Ответ верный.
Ответ верный.
Таким образом ответ 2 (Олег).
Дата добавления: 2018-05-12; просмотров: 4481; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

