Логическая операция ИНВЕРСИЯ (отрицание, логическое НЕ)
Инверсия(отрицание):
– в естественном языке соответствует словам «неверно, что...» и частице «не»;
– обозначение Ø А; 
– в языках программирования обозначается not.
Инверсия – это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.
Например, инверсией высказывания «Лондон – столица Франции» будет высказывание «Неверно, что Лондон – столица Франции».
В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.е. множеству получившемуся в результате отрицания множества А соответствует множество, дополняющее его до универсального множества.
Инверсия является унарной (одноместной) операцией: она выполняется над одним операндом.
Если значение логической переменной А истинно (равно 1), то значение Ā – ложно (равно 0) и наоборот: если значение А ложно, то значение Ā истинно.
Все остальные логические операции, рассматриваемые в данном пособии, являются бинарными (двуместными) и выполняются над двумя операндами.
Таблица истинности инверсии приведена в таблице 6, диаграмма Эйлера-Венна – на рисунке 5.
| U |
| Ā |
| A |
| |
| 0 | 1 | |
| 1 | 0 |
| Рисунок 5 – Диаграмма Эйлера-Венна для инверсии |
Логическая операция КОНЪЮНКЦИЯ (логическое умножение, логическое И)
|
|
|
Конъюнкция(от лат. conjunctio – соединение):
– в естественном языке соответствует союзу «и»;
– в алгебре высказываний обозначается &, Ù, *, · ;
– в языках программирования обозначается and.
Конъюнкция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Конъюнкцией элементарных высказываний «На улице прекрасная погода», «Мы пойдем на пляж» будет составное высказывание «На улице прекрасная погода и мы пойдем на пляж».
Таблица истинности конъюнкции приведена в таблице 7, диаграмма Эйлера-Венна – на рисунке 6.
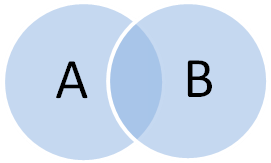Таблица 7 – Таблица истинности конъюнкции
| A | B | A&B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| A Ç B |
Рисунок 6 – Диаграмма Эйлера-Венна
для конъюнкции
В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству, получившемуся в результате умножения множеств А и В. Конъюнкции соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение, логическое ИЛИ)
|
|
|
Логическая операция дизъюнкция(логическое сложение):
– в естественном языке соответствует союзу «или»;
– в алгебре высказываний обозначается Ú, + ;
– в языках программирования обозначается or.
Дизъюнкция – это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.
Дизъюнкцией элементарных высказываний «Две прямые на плоскости параллельны», «Две прямые на плоскости пересекаются» будет составное высказывание «Две прямые на плоскости параллельны или пересекаются».
В алгебре множеств дизъюнкции соответствует операция объединения множеств, т.е. множеству получившемуся в результате сложения множеств А и В соответствует множество, состоящее из элементов, принадлежащих множеству А и элементов множества В.
Таблица истинности конъюнкции приведена в таблице 8, диаграмма Эйлера-Венна – на рисунке 7.
Таблица 8 – Таблица истинности дизъюнкции
| A | B | A v B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
| A |
| B |
А È В
|
|
|
Рисунок 7 – Диаграмма Эйлера-Венна
для дизъюнкции
Дата добавления: 2018-05-12; просмотров: 4549; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!