Число измерений (размерность) пространства.
Важную роль в дальнейшем будет играть понятие линейной зависимости и линейной независимости векторов.
Определение 1.2 Пусть  -- линейное пространство. Векторы  называются линейно зависимыми, если существуют такие числа 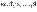 , из которых хотя бы одно отлично от нуля, что 
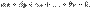
| (1) |
Векторы, не являющиеся линейно зависимыми, называются линейно независимыми. Другими словами,векторы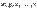 
называются линейно независимыми, если равенство
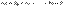
возможно только при 
.Пусть векторы 
линейно зависимы, т.е. пусть они связаны соотношением вида (1), в котором хотя бы один из коэффициентов, например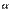 
, отличен от нуля. Тогда 
и, разделив на 
и положив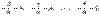 
получим: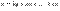 
|
Если вектор 
выражается через векторы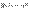 
в виде (2), то мы будем говорить, что 
есть линейная комбинация векторов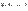 
.Таким образом, если векторы 
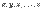линейно зависимы, то хотя бы один из них является линейной комбинацией остальных. Мы предоставляем читателю проверить, что верно и обратное, т.е. чтовекторы, один из которых есть линейная комбинация остальных, линейно зависимы.Определение 1.3 Линейное пространство 
называется 
-мерным, если в нем существует 
линейно независимых векторов и нет большего числа линейно независимых векторов. Если в пространстве 
можно найти любое число линейно независимых векторов, то 
называется бесконечномерным. Бесконечномерные пространства составляют предмет специального изучения. Мы будем в этой книге заниматься в основном пространствами конечного числа измерений. [document] В этой книге в основном рассматриваются пространства конечного числа измерений. Найдем в каждом из рассмотренных выше примеров 1-5 размерность соответствующего пространства. 1. Как мы уже указали, в пространстве 
примера 1 имеется три линейно независимых вектора, а всякие четыре вектора линейно зависимы. Поэтому трехмерно.2. 
-- пространство, векторами которого являются системы 
действительных чисел. В этом пространстве можно указать 
линейно независимых векторов, например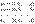 
(мы предоставляем читателю доказать, что эти векторы действительно линейно независимы).
|
|
|
Любой набор из N линейно независимых векторов называется базисом в пространстве RN . Простейший пример базиса — это набор векторов 
в каждом из которых только один элемент равен 1, а остальные равны нулю. Тогда любой вектор x = (x1, x2,...,xN)t может быть представлен как линейная комбинация x =x1e1+ x2e2+...+xNeN базисных векторов.
Базис, составленный из попарно ортогональных векторов, называется ортогональным, а если базисные вектора еще и нормированы, то этот базис называетсяортонормированным.
Дата добавления: 2018-05-12; просмотров: 170; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!