АКСИОМЫ ЛИНЕЙНЫХ ПРОСТРАНСТВ, ПРИМЕРЫ ЛИН. ПРОСТРАНСТВ
Nbsp;
ПОЛИНОМ
Многочлен (или полином) от n переменных — это конечная формальная сумма вида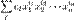 
,
где 
есть набор из целых неотрицательных чисел (называется мультииндекс), cI — число (называемое «коэффициент многочлена»), зависящее только от мультииндекса I.
В частности, многочлен от одной переменной есть конечная формальная сумма вида 
где ci фиксированные коэффициенты, а x — переменная. Функция вида
при 
и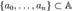 
относительно переменной 
называется полиномом1) илимногочленом от указанной переменной над множеством 
. Число 
называется коэффициентом2) полинома (при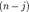 
-й степени переменной), выражение 
— членом (одночленом) полинома, 
— свободным членом, 
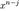— мономом.
Значением полинома при (или в точке)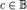 
называется число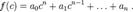 
Два полинома 
с коэффициентами из 
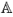называются (тождественно) равными: 
если совпадают множества их членов; или, что то же, равны их степени и равны коэффициенты при одинаковых степенях переменной. Это определение отличается от привычного определения равенства двух функций: две функции 
и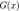 
называются равными на множестве 
если совпадают их значения при любом 
. На самом деле, для случая полиномов эти два определения — алгебраическое ифункциональное — эквивалентны. Корни
Если значение полинома 
при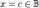 
равно нулю, то число 
ывается корнем полинома 
. Иными словами, корень полинома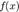 
— это решение уравнения 
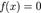, принадлежащее множеству .
|
|
|
Историческая справка. Корень как название неизвестной величины, которую требуется определить («извлечь») из уравнения, является переводом арабского слова «джизр» — буквально означающего «корень растения». В свою очередь, арабский вариант, по-видимому, является переводом санскритского слова «мула», применявшегося индийскими учеными для обозначения квадратного корня.
Уравнение 
, в левой части которого стоит полином одной или нескольких переменных, называется алгебраическим.
Задача. Выяснить количество корней полинома 
, принадлежащих множеству 
, и вычислить их.
Решить алгебраическое уравнение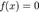 
над множеством 
означает найти все корни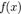 
, принадлежащие 
.
На основании теоремы из предыдущего пункта имеет место следующая
Теорема [Безу]. Пусть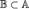 
и 
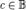— корень полинома 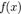. Тогда полином 
допускает представление в виде произведения: 
где полином 
определяется единственным образом.Итак, теорема Безу утверждает, что в случае существования корня полинома, возможно разложение этого полинома в произведение двух полиномов — одного первой степени и одного полинома степени, на единицу меньшей исходного. Тем самым, задача о нахождении корней полинома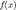 
сведется к аналогичной задаче для полинома 
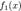; вторая задача может оказаться более простой за счет понижения степени.Фактическое нахождение полинома 
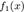возможно произвести с помощью схемы Хорнера.
|
|
|
Пример. Решить уравнение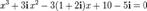 
над множеством 
, если известно, что число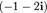 
— одно из его решений.
Решение. Строим схему Хорнера:
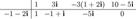
Видим, что число 
действительно является корнем полинома, и, следовательно, последний раскладывается в произведение двух полиномов: линейного и квадратичного. Коэффициенты квадратичного полинома выбираются из той же схемы:
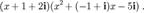
Квадратное уравнение над 
можно решить (см. ☞ ЗДЕСЬ ), его корн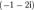и: 
и 
.
Ответ.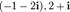 
.
Если полином 
раскладывается в произведение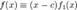 
, то полином 
называется линейным множителем для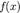 
над множеством 
.
АКСИОМЫ ЛИНЕЙНЫХ ПРОСТРАНСТВ, ПРИМЕРЫ ЛИН. ПРОСТРАНСТВ
Линейное, или векторное пространство 
над полем P — это непустое множество L, на котором введены операции(АКСИОМЫ)
сложения, то есть каждой паре элементов множества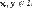 
ставится в соответствие элемент того же множества, обозначаемы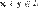й 
и
1. умножения на скаляр (то есть элемент поля P), то есть любому элементу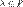 
и любому элементу 
ставится в соответствие единственный элемент из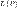 
, обозначаемый 
.
|
|
|
При этом на операции накладываются следующие условия:
, для любых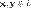 
(коммутативность сложения); 
, для любых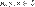 
(ассоциативность сложения);
1. существует такой элемент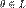 
, что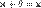 
для любого 
(существование нейтрального элемента относительно сложения), в частности L не пусто;
2. для любого существует такой элемент 
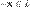, что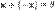 
(существование противоположного элемента относительно сложения).
3. 
(ассоциативность умножения на скаляр);
4. 
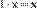(унитарность: умножение на нейтральный (по умножению) элемент поля P сохраняет вектор).
5. 
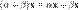(дистрибутивность умножения на вектор относительно сложения скаляров);
6. 
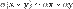(дистрибутивность умножения на скаляр относительно сложения векторов).
Элементы множества L называют векторами, а элементы поля P — скалярами. Свойства 1-4 совпадают с аксиомами абелевой группы.
Часто приходится встречаться с объектами, над которыми производятся операции сложения и умножения на числа. Приведем несколько примеров.1. В геометрии объектами такого рода являются векторы в трехмерном пространстве, т.е. направленные отрезки. При этом, если два направленных отрезка можно совместить параллельным переносом, то считается, что они определяют один и тот же вектор. Поэтому удобно все эти отрезки откладывать от одной какой-либо точки, которую мы будем называть началом координат. Операция сложения векторов, как известно, определяется следующим образом: суммой векторов 
и 
мы считаем диагональ параллелограмма со сторонам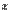и 
и . Известным образом вводится также умножение на числа.2. В алгебре мы встречаемся с системами 
чисел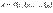 
(например, строки матрицы, совокупность коэффициентов линейной формы и т.д.). Для таких систем операции сложения и умножения на числа обычно определяются так: суммой систем 
и 
называется система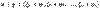 
. Произведением системы на число 
мы считаем систему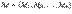 
.3. В анализе определяются операции сложения функций и умножения их на числа. В дальнейшем мы для определенности будем рассматривать совокупность всех непрерывных функций, заданных на сегменте 
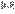.В приведенных примерах одни и те же операции сложения и умножения на числа производятся над совершенно разными объектами. Для того чтобы изучить все такие примеры с единой точки зрения, мы введем понятие линейного, или аффинного, пространства.
|
|
|
Дата добавления: 2018-05-12; просмотров: 297; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!