Тема1.4 Дифференциальные уравнения
Дифференциальным уравнением называется уравнение, связывающее независимую переменную, искомую функцию, её производную (или дифференциал независимой переменной и дифференциал функции)
Если дифференциальное уравнение содержит производную или дифференциал не выше первого порядка, то оно называется дифференциальным уравнением первого порядка.
Общий вид такого уравнения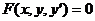 
. Общим решением дифференциального уравнения 1-ого порядка называется функция 
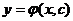, которая обращает это уравнение в тождество.
Частным решением дифференциального уравнения 1-ого порядка называется решение, полученное из общего решения при фиксированном значении С.
График любого частного решения дифференциального уравнения 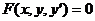называется интегральной кривой. Общему решению этого уравнения соответствует семейство интегральных кривых, зависящих от одного параметра.
Задача нахождения частного решения дифференциального уравнения 1-ого порядка при заданном начальном условии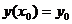 
называется задачей Коши. Это означает, что из всех интегральных кривых данного дифференциального уравнения требуется выделить ту, которая проходит через точку 
.
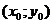Пример 1. Составить уравнение кривой 
, если угловой коэффициент касательной, проведённой в любой точке кривой, равен 2х.
Решение. На основании геометрического смысла производной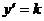 
, где k- угловой коэффициент касательной. Согласно условию k=2x . Составим дифференциальное уравнение первого порядка: 
.
|
|
|
Чтобы найти функцию надо проинтегрировать обе части уравнения.: 
, получили общее решение уравнения.
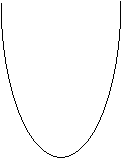
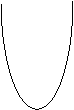
Геометрически это решение
представляет собой семейство
парабол с вершиной на оси ОУ,
симметричных относительно этой
оси.
Чтобы из общего решения
выделить частное решение, надо
задать начальные условия. Пусть
у=-1 при х=1, тогда общее решение
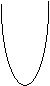
примет вид -1=1+с, 
с=-2. Геометрически частное решение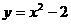 
представляет собой параболу, проходящую через точку (1;-1).
Дифференциальным уравнением первого порядка с разделяющимися переменными называется уравнение вида 
,где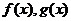 
заданные функции.
Алгоритм решения данного уравнения:
1) переписать производную через дифференциалы;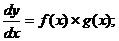 
2) разделить переменные
3) проинтегрировать обе части равенства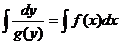 
и найти общее решение в виде функции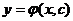
4) если заданы начальные условия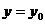 
при 
, то найти частное решение.
Пример 2. Найти общее решение дифференциального уравнения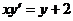 
Решение. Перепишем производную через дифференциалы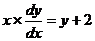 
. Разделим переменные 
. Проинтегрируем обе части равенства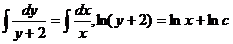 
(для удобства вместо постоянной с записали lnc). Применяя свойства логарифма, имеем 
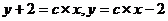, получили общее решение уравнения.
|
|
|
Пример 3. Решить уравнение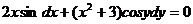 
, если 
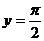при х=1
Решение Второе слагаемое переносим в правую часть равенства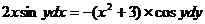 
обе части разделим на 
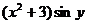, имеем: 
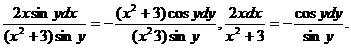Проинтегрируем обе части равенства 
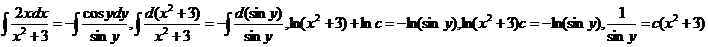-общее решение уравнения. Подставим начальные условия и найдём частное решение 
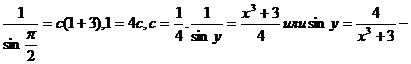частное решение.
Дата добавления: 2018-05-12; просмотров: 310; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!