КОНВЕКТИВНЫЙ ТЕПЛООБМЕН (ТЕПЛООТДАЧА)
Процесс теплообмена между поверхностью твердого тела и жидкостью, имеющих разные температуры, называется теплоотдачей. Теплоотдача обычно сопровождается теплопроводностью. Совместный процесс конвекции и теплопроводности называется конвективной теплоотдачей.
Согласно закону Ньютона-Рихмана тепловой поток в процессе теплоотдачи пропорционален коэффициенту теплоотдачи, площади поверхности теплообмена и разности температур поверхности тела и жидкости.
Q =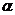 
(tс – tж)F , 2.17
В расчетах разность температур tс – tж берут по абсолютной величине. Коэффициент теплоотдачи α Вт/(м2·К) характеризует интенсивность процесса теплоотдачи и зависит от большого числа факторов:
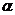= ƒ ( tж, t ст, d, λ, ν, ω, ℓ, ġ, β Х…….) 2.18
где : tж-температура жидкости,0С ; tст – температура стенки, 0С; d –диаметр трубы, м;
λ – теплопроводность жидкости, Вт/ ( м К ): ω –скорость течения жидкости, м/с; ℓ – определяющий размер ( для труб – диаметр ), м ; g – ускорение свободного падения, 9,8 м/с2 ;
β – коэффициент объемного расширения, 1/К ; Х – характер течения жидкости; ν – кинематический коэффициент вязкости, м2/с.
Из формулы 2.18 видно, что коэффициент теплоотдачи определить сложно, т.к. он зависит от большого числа переменных.
Существует два способа решения задач конвективного теплообмена: аналитический и с применением теории подобия.
|
|
|
При аналитическом решении задач конвективного теплообмена составляются дифференциальные уравнения, учитывающие тепловые и динамические явления в рассматриваемом процессе. Вывод таких уравнений рассматривается в специальной литературе.
Конвективный теплообмен в несжимаемой однофазной среде описывается следующими уравнениями.
Уравнение теплоотдачи:
α = -( λ/θ ) ( ∂t / ∂n )n=0, где θ = t – t0. 2.19
Дифференциальное уравнение теплопроводности (сплошности) имеет вид:
∂t /∂τ = а 
2t = [∂ 2t / ∂x2 +∂2t / ∂y2 + ∂2t / ∂z2 ] λ /с ρ 2.20
где: ∂t /∂τ – температурное поле исследуемого объекта, которое зависит от изменения температуры по осям , т.е. от оператора Лапласа,
2t = ∂2t /∂x2 + ∂2t / ∂y2 + ∂2t /∂ z2, 2.21
и от теплофизических свойств: коэффициента температуропроводности – а (м2/с), удельной теплоемкости – с (кДж/(кг К) и плотности ρ (кг/м3)
Дифференциальное уравнение движения:
∂ω/ ∂τ = gβ 
– 1/ρ ( ρ) + ν 2ω. 2.22
Дифференциальное уравнение сплошности: 
|
|
|
∂ωх / ∂х + ∂ωу / ∂у + ∂ωz / ∂z = 0 или div = 0 2.23
Приведенные дифференциальные уравнения конвективного теплообмена 2.19 – 2.22 описывают бесчисленное множество процессов. Чтобы решить конкретную задачу, к приведенным уравнениям следует присоединить условия однозначности. Условия однозначности дают математическое описание частных случаев. Условия однозначности состоят:
1)из геометрических условий, характеризующих форму и размеры тела или системы, в которой протекает процесс;
2) физических условий, характеризующих физические свойства среды;
3) граничных условий, определяющих особенности протекания процесса на границах жидкой среды;
4) временных или начальных условий, характеризующих особенности процесса в начальный момент времени; для стационарных процессов эти условия отпадают.
Решение приведенных систем дифференциальных уравнений и условий однозначности с большим количеством переменных получается сложным. Поэтому большое значение приобретает экспериментальный путь исследования и применение теории подобия.
В основе теории подобия лежат три теоремы.
Первая терема подобия: у подобных явлений числа подобия численно одинаковы.
|
|
|
Вторая теорема подобия: если физическое явление описывается системой дифференциальных уравнений, то всегда существует возможность представить их в виде уравнений подобия.
Третья теорема подобия: подобны те явления, условия однозначности которых подобны, и числа подобия, составленные из условий однозначности, численно одинаковы.
Сущность теории подобия состоит в том, что размерные физические величины, влияющие на конвективный теплообмен, объединяются в безразмерные комплексы, причем так, что число комплексов меньше числа величин, из которых составлены эти комплексы. Комплексам или числам подобия присваиваются имена ученых, внесших большой вклад в исследование процессов теплопереноса и гидродинамики
Полученные безразмерные комплексы рассматриваются как новые переменные. Они отражают не только влияние одиночных факторов, но и их совокупности, что упрощает описание исследуемого процесса. Теория подобия является теоретической базой эксперимента, облегчает анализ процессов. Рассмотрим применение теории подобия для исследования конвективных процессов теплоотдачи.
Из формулы 2.17 видно, интенсивность конвективного теплообмена характеризуется коэффициентом теплоотдачи, который зависит, в частности, от определяющего размера, площади теплообменной поверхности, температуропроводности, теплопроводности, температурного напора, скорости движения жидкости, коэффициента кинематической вязкости и т. д.
|
|
|
Из этих величин составлены безразмерные комплексы – числа подобия (критерии подобия).
число Нуссельта Nu = αℓ / λ 2.24
число Рейнольдса Re = ωℓ / ν 2.25
число Грасгофа Gr = g β Δt ℓ3/ ν2 2.26
число Прандтля Рr = ν /а 2.27
Число Нуссельта – определяемое число, т.к. в него входит искомый коэффициент теплоотдачи. Числа Рейнольдса, Грасгофа, Прандтля – определяющие. Они состоят из величин, известных до решения задачи. В общем виде
Nu= ƒ ( Rе, Gr, Рr ) 2.28
Для решения задач приведенное уравнение записывается в степенном виде:
Nu = c Rеm Grn Рrr 2.29
Различают естественное (свободное) и вынужденное течение жидкости.
Естественная конвекция возникает за счет разности плотностей холодных и горячих частиц жидкости около поверхности нагрева. Интенсивность теплового расширения характеризуется температурным коэффициентом объемного расширения β Для газов, которые в большинстве случаев можно считать идеальными, коэффициент объемного расширения определяется равенством
β = 1/Т 2.30
При естественной конвекции уравнение 2.28 упрощается:
Nu= с ( Gr, Рr )n 2.31
Вынужденная конвекция создается внешним источником (насосом, вентилятором). Для вынужденной конвекции уравнение 2.28 имеет вид:
Nu = с Rеm Prn 2.32
Задачей эксперимента является определение конкретного вида функциональной связи в уравнении подобия, т.е. следует найти числовые значения коэффициентов, показателей степеней и т.д.
Определив число Нуссельта, можно рассчитать искомый коэффициент теплоотдачи:
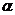= Nu ℓ /λ 2.33
Как показали экспериментальные исследования, режим течения определяется скоростью потока.
О. Рейнольдс опытным путем установил, что при движении жидкости встречаются два вида потока, подчиняющимся различным законам. В одном виде потока все частицы движутся только по параллельным траекториям и движение длительно совпадает с направлением всего потока. Жидкость движется спокойно, без пульсаций. Такое движение названо ламинарным. При ламинарном течении в трубе число Рейнольдса менее 2300.
Во втором типе потока происходит непрерывное перемешивание всех слоев жидкости. Поток представляет беспорядочную массу хаотически движущихся частиц. Такой тип потока называется турбулентным. При турбулентном течении число Рейнольдса более 104.
При числах Рейнольдса более 2000, но менее 1.104 движение жидкости нестабильное. Режим течения называется переходным.
Теоретическое исследование задач конвективного теплообмена основано на теории пограничного слоя, разработанной Л. Прандтлем.
Введены понятия теплового и динамического пограничных слоев.
Если температуры стенки и жидкости неодинаковы, то вблизи стенки образуется тепловой пограничный слой, в котором происходит изменение температуры. Вне пограничного слоя температура жидкости одинакова и равна температуре потока.
Тонкий пограничный слой жидкости вблизи поверхности, в котором происходит изменение скорости от значения скорости невозмущенного потока вдали от стенки до нуля непосредственно на стенке, называется динамическим пограничным слоем.
Рис.2.4 Распределение температуры и скорости в тепловом
и динамическом пограничном слое
С увеличением вязкости толщина динамического слоя увеличивается, с увеличением скорости потока толщина динамического слоя уменьшается. Течение в динамическом слое может быть как ламинарным, так и турбулентным и определяется числом Рейнольдса.
Толщины теплового и пограничного слоев могут не совпадать. Соотношение толщин динамического и теплового пограничных слоев определяется безразмерным числом Прандтля. Для вязких жидкостей, например, масел, Рr>1. Для вязких жидкостей, например, масел толщина динамического пограничного слоя больше толщины теплового пограничного слоя. Для газов Рr ≈ 1и толщины слоев приблизительно одинаковы. Для жидких металлов Рr < 1, толщина теплового пограничного слоя больше толщины динамического пограничного слоя.
Если движение внутри теплового пограничного слоя ламинарное, то теплообмен осуществляется теплопроводностью. С увеличением скорости в пограничном слое и появлением турбулентности следует учитывать интенсивность перемешивания жидкости.
В процессе продольного обтекания какого-либо тела безграничным потоком жидкости с постоянной скоростью течения в непосредственной близости от поверхности тела скорость течения должна падать до нуля.
При решении задач конвективного теплообмена следует обращать внимание на то, какая температура для данного уравнения подобия принимается за определяющую, т.к. физические параметры жидкостей и газов изменяются с изменением температуры.
Для простейших случаев, когда температура потока изменяется в небольших пределах, среднюю температуру жидкости можно определить как среднеарифметическую у входа в канал t1 и выхода из канала t2: tж = 0,5 (t1 – t2).
Для более точных расчетов пользуются формулой
tж = 0, 5 ( t1 – t2 ) 
( ∆tб - ∆tм)/ ℓn ( ∆t б /∆tм ), 2.34
где ∆ tб и ∆ tм – температурные напоры в начальном и конечном сечении трубы или канала.
В некоторые числа подобия входит линейный размер, причем, берут тот размер, которым определяется развитие процесса. Для труб определяющим размером при течении жидкости внутри трубы является внутренний диаметр, при внешнем обтекании – наружный диаметр трубы, для каналов некруглого сечения - принимается эквивалентный диаметр dэкв = 4F / S, где F – площадь поперечного сечения канала, S – полный (смоченный) периметр канала. При обтекании плиты за определяющий размер принимается ее длина по направлению движения потока.
Следует обратить внимание на аналогию процессов тепло и массопереноса.
Рассмотренное выше уравнение теплопроводности – закон Фурье (уравнение 2.3) аналогичен основному закону процесса диффузии (молекулярного переноса массы) – закону Фика.
m = - D grad ci 2.35
где m плотность потока массы, кг / ( м2 с ); D – коэффициент диффузии, м2/ с; сi – концентрация массы рассматриваемого компонента в единице объема вещества, кг/м3. Сопоставим эти законы:
Q = -λgrad t F m = - D grad ci F
Одинаковые математические записи законов Фурье и Фика отражают аналогию переноса массы и теплоты. Например, в газах носители массы и теплоты одни и те же: Каждая молекула вместе с собственной массой переносит и энергию. Вблизи поверхности образуется тонкий пограничный слой, в котором концентрация вещества будет изменяться от состояния насыщения у поверхности до концентрации вещества в потоке.
Уравнение массоотдачи в направлении у (поперек потока) имеет вид
β = ( D / c 0- c ж ) (∂с / ∂у ) 2.36
Уравнение переноса массы диффузией и концентрацией
ωх (∂с /∂х ) + ωу( ∂с/∂у) = D [(∂2c/∂х2) + ( ∂2с/∂у2) 2.37
Уравнения сплошности и движения (2.20 и 2.22) останутся без изменения.
Аналогичны по записи числа Nu и Рr
Nu =αℓ/λ Nuд= βℓ/ D – иногда его называют числом Шервуда 2.38
Рr = ν/ а Рrд = ν/ D - иногда его называют числом Шмитда 2.39
Nu = Nuд; Рr = Рrд 2.40
Одни и те же безразмерные уравнения при одних и тех же граничных условиях дадут одни и те же решения, пригодные для описания процессов как теплоодачи, так и массоодачи.
βℓ / D = αℓ/λ , тогда 2.41
β / D = α / λ 2.42
При больших перепадах температур или концентраций аналогия процессов тепло и массообмена нарушается, т.к. зависимости теплофизических свойств от температуры и концентрации неодинаковы.
Дата добавления: 2018-05-12; просмотров: 1117; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!