Колебательные системы. Свободные колебания в одиночном контуре.
В различных радиотехнических устройствах, особенно врадиоприемных, одной из важнейших операций является выделение полезного сигнала из всевозможных помех. Эти функции выполняются электрическими колебательными системами, основным элементом которых является колебательный контур. При изучении свойств колебательного контура главное внимание обращается на его резонансные свойства, которые и определяют его частотную избирательность. В зависимости от способа включения элементов колебательного контура индуктивности L и емкостиС по отношению к внешнему источнику сигнала различают последовательный и параллельный колебательные контуры.
При отсутствии внешнего возбуждения в колебательном конуре с первоначально запасённой энергией электрического поля в конденсаторе или магнитного поля в индуктивности возможно существование свободных колебаний.
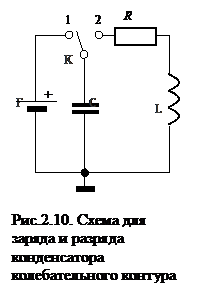Рассмотрим переходные процессы в цепи, состоящей из индуктивности L, емкости C и активного сопротивления R, рис. 2.10. Если предварительно зарядить конденсатор C, а затем в момент времени t=0 замкнуть его на цепь состоящей из последовательно включенныхL и R, то в таком контуре будет идти процесс периодического преобразования электрической энергии в магнитную и наоборот. В этом случае функция внешнего воздействия при любых t0³ 0 равна нулю и уравнение Кирхгофа для такой цепи имеет вид 
(2.27)
После дифференцирования соотношение (2.27) по времени и деления на L обеих частей этого уравнения запишем для тока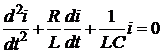 
(2.28)
|
|
|
Введем параметры 
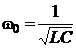или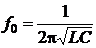 
(2.29)
Тогда с учетом соотношения (2.29) выражение (2.28) принимает вид 
(2.30)
Решение дифференциального уравнения (2.30) будем искать в виде 
(2.31)
Подстановка решения уравнения (2.31) в выражение (2.30) приводит к соотношению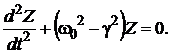 
(2.32). Обозначим 
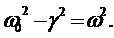(2.33)
С учетом соотношения (2.33) выражение (2.32) принимает вид 
(2.34)
Решением уравнения (2.34) является функция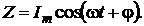 
(2.35)
После подстановки зависимости (2.35) в выражение (2.31) для тока і получим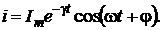 
(2.36)
Из уравнения (2.36) следует, что ток в колебательном контуре изменяется по гармоническому закону, причем его амплитуда с течением времени непрерывно уменьшается. Затухание амплитуды тока аналитически описывается множителем e-gt. Скорость затухания собственных колебаний в контуре можно охарактеризовать отношением амплитуд тока в моменты времени t и t+T (рис. 2.11), гдеТ – период колебаний.
Используя выражение (2.36) находим это соотношение записать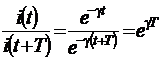 
(2.37)
Натуральный логарифм выражения (2.37) носит название логарифмического декремента затухания контура, и для контура с малыми потерями описывается формулой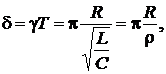 
(2.38) где 
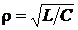– волновое или характеристическое сопротивление контура.
|
|
|
На практике вместо логарифмического декремента затухания (2.38) часто используется пропорциональная ему величина – затухание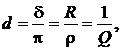 
(2.39)
где величина, равная Q=r/R (2.40)называется добротностью контура.
С энергетической точки зрения добротность контура характеризует отношение запасенной электромагнитной энергии контура при резонансе к энергии, поглощаемой в этом режиме активным сопротивлением контура за один период изменения тока в контуре. Добротность Q контура с малым затуханием может быть достаточно просто определена путем подсчета по осциллограмме числа периодов свободных колебаний в контуре числа m периодов колебаний за интервал времени, в течение которого амплитуда собственных колебаний контура уменьшается в два раза. Тогда согласно соотношению (2.37)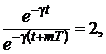 
или egmТ=2, откуда gmТ=ln2. Логарифмический декремент затухания согласно выражению (2.38) равен d=gT=ln2/m, а затухание на основании соотношения (2.39) d=d/p=ln2/pm. Отсюда добротность контура 
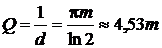(2.41)
Дата добавления: 2018-05-12; просмотров: 316; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!