Спектральный состав последовательности прямоугольных импульсов при различном периоде их скважности.

Классификация сигналов и их параметры.

Электрические сигналы представляют собой электрические процессы, используемые для передачи или хранения информации.

Сигналы можно разделить на два больших класса: детерминированные и случайные. Детерминированными называются сигналы, мгновенные значения которых в любой момент времени можно предсказать с вероятностью, равной единице и которые задаются в виде некоторой определенной функции времени. Приведем несколько характерных примеров: гармонический сигнал с известной амплитудой A и периодом T (рис. 1.1 а); последовательность прямоугольных импульсов с известным периодом следования T, длительностью t_ии амплитудой A (рис. 1.1 б); последовательность импульсов произвольной формы с известнымидлительностью t_и, амплитудой A и периодом T (рис. 1.1 в). Детерминированные сигналы не содержат никакой информации.

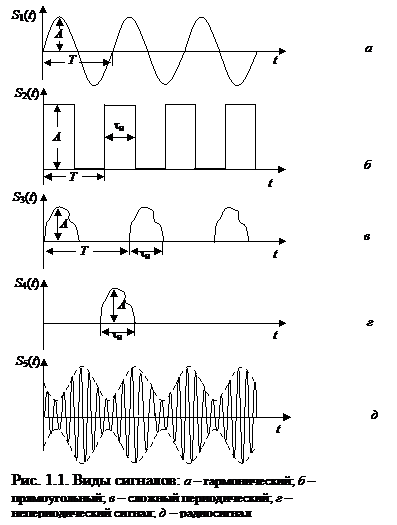Случайные сигналы представляют собой хаотические функции времени, значения которых заранее неизвестны и не могут быть предсказаны с вероятностью, равной единице (одиночный импульс с длительностью t_ии амплитудой A (рис. 1.1 г) речь, музыка в выражении электрических величин). К случайным сигналам относятся также шумы.

Детерминированные сигналы, в свою очередь, подразделяются на периодические, для которых выполняется условие S(t)=S(t+kT), где T – период, k -любое целое число, а под S(t) понимается изменяющиеся со временем ток, напряжение или заряд (рис. 1.1 а, б, в).

Очевидно, что к непериодическим относится любой детерминированный сигнал, для которого выполняется условие S(t)¹S(t+kT).

Простейшим периодическим сигналом является гармонический сигнал вида .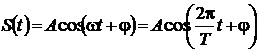

Любой сложный периодический сигнал можно разложить на гармонические составляющие. Ниже такое разложение будет проведено для нескольких конкретных видов сигналов.

Гармонический сигнал высокой частоты, в котором путем модуляции заложена информация, называется радиосигналом (рис. 1.1 д).

Периодические сигналы.

Любой сложный периодический сигнал S(t)=S(t+kT) (рис.1.2), заданный на интервале значений t от –¥ до +¥, может быть представлен в виде суммы элементарных гармонических сигналов. Это представление осуществляется в виде ряда Фурье, если только заданная периодическая функция удовлетворяет условиям Дирихле:

1. На любом конечном интервале времени функция S(t) должна быть непрерывна или иметь конечное число разрывов первого рода.

2. В пределах одного периода функция должна иметь конечное число максимумов и минимумов.

Обычно все реальные радиотехнические сигналы удовлетворяют этим условиям. В тригонометрической форме ряд Фурье имеет вид (1.1)

где постоянная составляющая равна 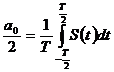(1.2)

а коэффициенты a_n, и b_n при косинусоидальных и синусоидальных членах разложения определяются выражениями 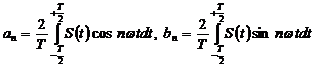(1.3)

Амплитуда (модуль) и фаза (аргумент) n-ой гармоники выражаются через коэффициенты a_n, и b_n следующим образом (1.4)

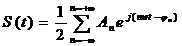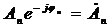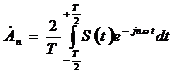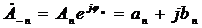При использовании комплексной формы записи выражение для сигнала S(t) принимает вид . Здесь коэффициенты , называемые комплексными амплитудами, равны и связаны с величинами а_nи b_nформулами: при n>0, и при n<0. С учётом обозначений .

Спектр периодической функции состоит из отдельных линий, соответствующих дискретным частотам 0, w, 2w, 3w …, т. е. имеет линейчатый или дискретный характер (рис.1.3). Использование рядов Фурье в сочетании с принципом суперпозици является мощным средством анализа влияния линейных систем на прохождение через них различного вида периодических сигналов.

При разложении периодической функции в ряд Фурье, следует учитывать симметрию самой функции, т. к. это позволяет упростить расчеты. В зависимости от вида симметрии представленные рядом Фурье функции могут:

1. Не иметь постоянной составляющей если площадь фигуры для положительного полупериода равна площади фигуры для отрицательного полупериода.

2. Не иметь четных гармоник и постоянной составляющей, если значения функции повторяются через половину периода с обратным знаком.

3. Содержать только косинусоидальные составляющие если функция четная относительно времени t т. е. f(t)=f(–t) (симметрия относительно оси ординат).

4. Содержать только синусоидальные составляющие, если функция нечетная, т. е. f(t)=–f(–t) (симметрия относительно начала координат).

Спектральный состав последовательности прямоугольных импульсов при различном периоде их скважности.

Периодическая последовательность прямоугольных импульсов изображена на рис. 1.4. Постоянная составляющая ряда Фурье определяется из выражения 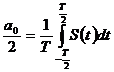и для данного случая равна .

Амплитуда cos-составлящей а_n равна

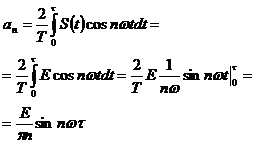, а амплитуда sin-составляющей b_nравна .

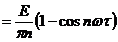Амплитуда n-ой гармоники

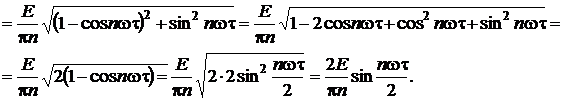
Амплитуда n-ой гармоники зависит от величины 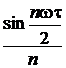т. е. изменяется согласно этому закону.

Определим номера гармоник n₀, которые обращаются в нуль. Это возможно, если 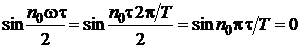, откуда 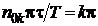, k=1, 2, 3, …, и 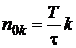. Определим далее соответствующие «нулевые» частоты, т. е. те частоты, на которых амплитуда равна нулю . .

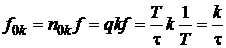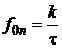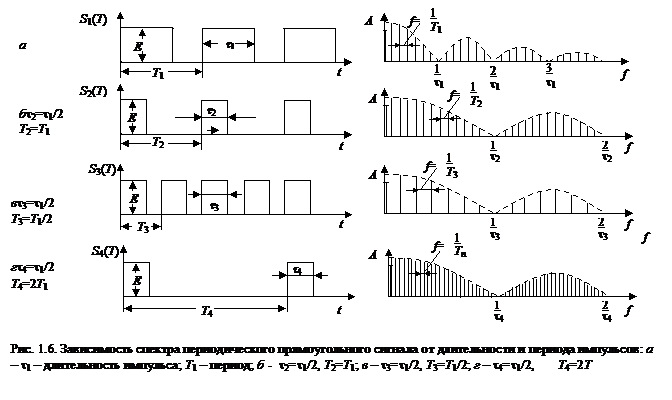
Вид спектра такой последовательности показан на рис 1.5. Изобразим вид спектра последовательностей с различными параметрами t иТ (рис. 1.6).

Скважность— один из классификационных признаков импульсных систем, определяющий отношение периода следования (повторения) импульсов одной последовательности к их длительности.

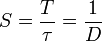
где S — скважность, D — коэффициент заполнения, T — период импульсов, τ — длительность импульса.

Дата добавления: 2018-05-12; просмотров: 1104; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!