Бесконечно малые и б.б. числовые последовательности, связь между ними.
Теорема 1. : Сходящаяся числ. последовательность ограничена.
Т.2: Ограниченная монотонная ч. п. сходится.
Если Lim an=0 , то ч.п.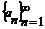 
называется б.м.
Пример: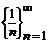 
; 
; 
.
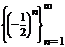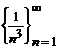Ч.п. называется б.б. и обознач.: Lim an=∞
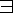
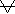nà∞
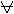если: M>0 N такой, что n>N, выполняется: (an)>M.
пример: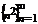 
; 
.
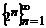Т.3:
А) если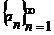 
- б.м. ч.п. и an≠0, то 
- б.б. ч.п. [1/0=∞]
Б) если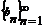 
- б.б. ч.п. и bn ≠0, то 
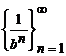- б.м. ч.п. [1/∞=0].
Предел ф-ции(2 опред.):
1-ое опред.(на языке последовательностей(по Гейне)): Число А наз-ся пределом ф-ции f(x) в точке X0 
, если 
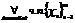на множестве X выполняется:
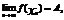
2-ое опред.(на языке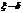 
(эпсилам-дельта) по Коши):
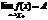, если: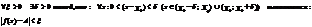 
Односторонние пределы и пределы по бесконечному направлению
Односторонние пределы:
1) 
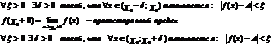
Теорема 1: Оба определения предела ф-ции в точке эквивалентны.
Теорема 2: Предел ф-ции X0 тогда и только тогда, когда существуют оба односторонних предела и они равны между собой.
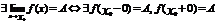
Пределы по бесконечному направлению:
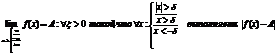
1) Если 
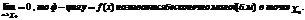
2) Ф-ция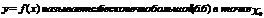 
:
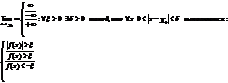
Бесконечно малые и бесконечно большие ф-ции в точке, их св-ва:
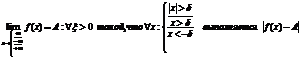
1) Если 
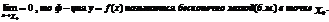
2) Ф-ция 
:
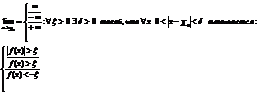
Свойства:
Теорема 1:
1) Если f(x)-б.м. ф-ция в т. 
2) Еслиg(x)-б.б. ф-ция в т.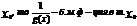 
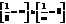
Теорема 2:
Если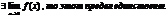 
Теорема 3:
Сумма, разность и произведение б.м. ф-ций в т.X0 является б.м. ф-цией в т. X0.
Произведение б.м. в т. X0 на ограниченную, явл. б.м.
Теорема о пределах ф-ции в точке:
Если 
:
1) 
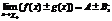
2) 
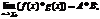
3) 
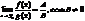
Классификация бесконечно малых функций
|
|
|
Пусть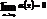 
и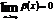 
.
Вычисляем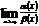 
.
Если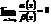 
, то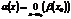 
- бесконечно малая функция более высокого порядка малости, чем 
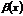. Пример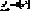 
Если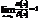 
, то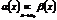 
- б.м. функции эквивалентны в т. X0
Если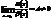 
, то 
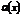и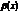 
- одного порядка малости в т. X0. Пример 5x2и3x2.
Замечательные пределы
1-й замечательный предел:
Пример: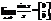 
1) 
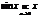
2) 
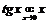
3) 
2-й замечательный предел:
Пример: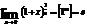 
Непрерывность ф-и в точке. Классиф. точек разрыва. Св-ва ф-й, непрерывность в точке и на отрезке.
Y=f(x) по обл Д Xo €Д Xo+∆X€Д ∆X – приращение аргумента
∆f(x)=f(Xo+∆X) – f(Xo) - приращение ф-и в точке Xo
Ф-я y=f(x), наз. Непрерывной в точке Xo если: 1) Xo€Д т.е.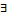 
f(Xo); 2) 
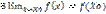; 3)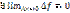 
(б.м. приращение по аргументу 
соотв. Б.м. приращение аргумента ∆f)
Точки в которых нарушается непрерывность, наз. точками разрыва.
Классиф. точек разрыва: Вычислим: пусть Хо – т.разрыва, f(Xo-0) и f(Xo+0) – односторонние пределы.
1)Если однос.пределы f(Xo-0)=A и f(Xo+0)= В – конечны, то Хо наз.точкой разрыва 1-го рода.
2)В частности, если А=В(но ≠f(Хо), то Хо, наз.точкой устранённого разрыва.
3)Все остальные точки разрыва(хотябы один из одност. пределов бесконечны или не сущ.)и точки разрыва 2-го порядка.
|
|
|
 |
F(x) = 
Х=0,т.разрыва 2-го рода 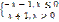F(x)=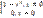 
F(x)= 
f(x)=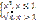 
X=0,т.разрыва 1-го рода x=0, т.устран.разрыва x=1, точка непрерывности
Ф-я f(x) наз.непрер.на отрезке АВ, если она непрерывна в каждой т.этого отрезка.
Св-ва ф-й, непрер.на отрезке: Т1(Вейерштрасса):если ф-я f(x) непрер.на отрезке АВ, то она достигает на этом отрезке наибол.(М) и наимен.(м) значений.
Т2: если ф-я непрер. На отрезке АВ и принимает на концах отрезка значение разных знаков, т.е. f(a)*f(b)<0,то сущ. C€(a,b) такой, что f(c)=0
Т3: если ф-я f(x) непрер. На отрезке АВ и приним. значение между м и М, то для любого числа C€(a,b) такое, что f(c)=c
Теорема: все остальн. Элементы ф-и( степенная, показательная, логарифмическая, тригоном. и обратн. тригоном)непрер. на своей облости определения. Пример: док-ть, что ф-я f(x)=2+3x-x2 непрер. на(-∞;+∞)
|
|
|
2’) 
; 
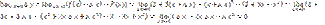
Дата добавления: 2018-05-12; просмотров: 293; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!