Generierung allgemeiner Trajektorien durch
Interpolationspolynome
69. Wenn die Trajektorie q(t) bzw. x(t), die Bahn q(s) bzw. x(s) oder das Geschwindigkeitsprofil s˙(t) in diskreten Punkten gegeben sind, kann das Problem der Trajektorien bzw. Bahnplanung auf die Approximation von Funktionen bei gegebenen Stützstellen zurückgeführt werden.
70. Dazu wird das Zeitintervall [0, T] durch eine eigentlich monoton wachsende Folge von diskreten Zeitpunkten  mit
mit  in N Teilintervalle
in N Teilintervalle 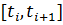 zerlegt.
zerlegt.
71. Bild 7.5 zeigt für den skalaren Fall 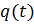 das Vorgehen.
das Vorgehen.
72. Durch 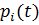 werden die Approximationspolynome bezeichnet.
werden die Approximationspolynome bezeichnet.
73. Bild 7.5: Approximation durch Polynome 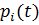 .
.
74. Je nach Anforderungen an die Stetigkeit von 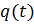 müssen neben den Funktionswerten
müssen neben den Funktionswerten  noch die Ableitungen
noch die Ableitungen 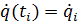 bzw.
bzw.  in den Stützstellen bekannt sein, dargestellt durch das folgende Schema:
in den Stützstellen bekannt sein, dargestellt durch das folgende Schema:
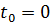
| 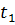
| 
| … | 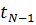
| 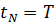
| |
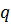
| 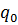
| 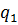
| 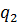
| … | 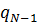
| 
|
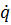
| 
| 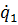
| 
| … | 
| 
|
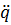
| 
| 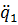
| 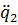
| … | 
| 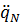
|
75. Als Approximationspolynome werden Minimalpolynome verwendet, das sind solche, deren Polynomgrad sich aus der eindeutigen Berechenbarkeit der Polynomkoeffizienten ergibt.
1. Generierung 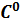 -stetiger Trajektorien
-stetiger Trajektorien
76. Diese sind durch ihre einfache Stetigkeit gekennzeichnet und können durch Polynome ersten Grades approximiert werden.
77. Die Randbedingungen lauten
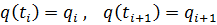 .
.
78. Für den Ansatz
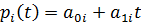
ergeben sich die Koeffizienten 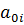 ,
, 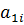 durch Einsetzen der Randbedingungen als Lösung eines linearen Gleichungssystems
durch Einsetzen der Randbedingungen als Lösung eines linearen Gleichungssystems
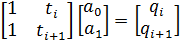 .
.
79. Das in Beispiel 7.2 behandelte trapezförmige Geschwindigkeitsprofil ist eine typische 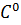 -stetige Trajektorie.
-stetige Trajektorie.
2. Generierung 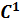 -stetiger Trajektorien (Stoßfreie Trajektorien)
-stetiger Trajektorien (Stoßfreie Trajektorien)
80. Sie sind durch ihre Stetigkeit bis zur ersten Ableitung gekennzeichnet.
81. Die Randbedingungen lauten in diesem Fall
|
|
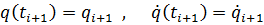 .
.
82. Das Minimalpolynom muß 3. Grades sein,
|
|
83. Die Koeffizienten 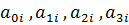 ergeben sich in analoger Weise aus dem Gleichungssystem
ergeben sich in analoger Weise aus dem Gleichungssystem
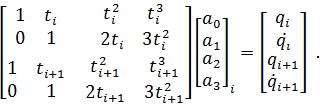
3. Generierung 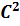 -stetiger Trajektorien (Ruckfreie Trajektorien)
-stetiger Trajektorien (Ruckfreie Trajektorien)
84. Randbedingungen:
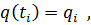
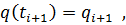
| |
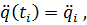
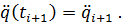
85. Minimalpolynom:
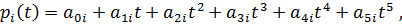
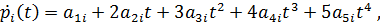
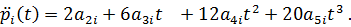
86. Bestimmung der Polynomkoeffizienten aus dem Gleichungssystem:
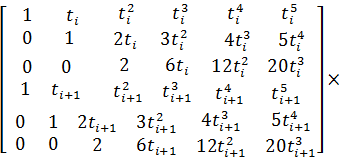

Beispiel 7.3: Ruckfreie Beschleunigungsphase
87. Will man z.B. die Beschleunigungsphase von Bild 7.3b ruckfrei durchführen, lauten die Randbedingungen 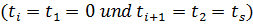 :
:
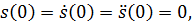
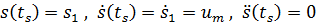 .
.
88. Für die Polynomkoeffizienten erhält man aus dem oben angegebenen Gleichungssystem
|
|
|
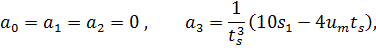
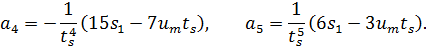
89. Die ruckfreie Bahn kann folglich durch beschrieben werden
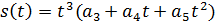 .
.
Beispiel 7.4: Verbindung von Geradenstücken durch Polynome 3. Grades (Bild 7.6)
90. Die Trajektorie sei durch N Geradenstücke gegeben.
91. Um die Unstetigkeiten der ersten Ableitungen zu den Zeitpunkten
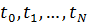 zu vermeiden, werden häufig die durch lineare Interpolation entstehenden Ecken durch Polynome 2. oder 3. Grades ersetzt.
zu vermeiden, werden häufig die durch lineare Interpolation entstehenden Ecken durch Polynome 2. oder 3. Grades ersetzt.
92. Die Generierung C1-stetiger Verläufe läßt sich mit einer kleinen Modifikation durch Gl. (7.8) ausführen.
93. Dazu müssen in Gl. (7.8) 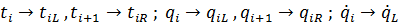 und
und 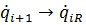 ersetzt werden.
ersetzt werden.
94. Bild 7.6: Gemischte Interpolation
7.1.4 Bahnplanung für redundante Systeme
95. Nach Abschnitt 6.1.6 besitzt ein redundantes MKS mehr Freiheitsgrade als für die Ausführung der Aufgabe notwendig ist (n > m).
96. Das inverse kinematische Problem liefert in diesem Fall mehrdeutige Lösungen, d.h. jeder Bahnpunkt kann mit unendlich vielen Konfigurationen erreicht warden.
97. Die Auswahl einer ”geeigneten“ Konfiguration kann z.B. über eine Optimierungstrategie erfolgen.
98. Im einfachsten Fall dient dazu ein Gütekriterium der Form
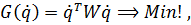
das die verallgemeinerten Geschwindigkeiten mit einer symmetrischen, positiv definiten (n, n)-Wichtungsmatrix 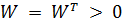 quadratisch wichtet.
quadratisch wichtet.
99. Die ”geeignete“ Konfiguration ist dadurch ausgezeichnet, daß sie eine Lösung des Problems
a) mit kleinstem quadratischen Geschwindigkeitsaufwand liefert und
b) die Nebenbedingung (6.41) erfüllt.
100. Die Lösung dieser Extremalaufgabe mit Nebenbedingung kann mit der Methode der Lagrangeschen Multiplikatoren erfolgen.
101. Dazu wird das um die Nebenbedingung in impliziter Form erweiterte Gütekriterium
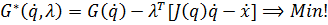
betrachtet.
102. Der Vektor 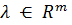 heißt Lagrangescher Multiplikator.
heißt Lagrangescher Multiplikator.
103. Die notwendigen Bedingungen für die Existenz eine Minimums ergeben
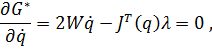
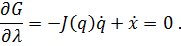
104. Aus diesen Beziehungen können berechnet und die inverse Kinematik gelöst werden.
105. Aus der ersten Gleichung folgt
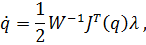
Einsetzen in die zweite Gleichung und Auflösen ergibt für den Lagrangeschen Multiplikator
|
|
|
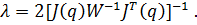
106. Diese Auflösung ist möglich, da  den vollen Rang besitzt und folglich invertierbar ist.
den vollen Rang besitzt und folglich invertierbar ist.
| 107. Durch Elimination von findet man schließlich das Ergebnis
|
mit der die inverse Kinematik redundanter MKS behandelt werden kann.
108. Die hinreichende Bedingung für die Existenz eines Minimums
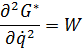
ist wegen 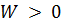 stets erfüllt.
stets erfüllt.
109. Der Sonderfall 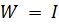 führt auf
führt auf
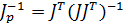
mit 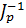 als der rechten Pseudoinversen von J.
als der rechten Pseudoinversen von J.
Дата добавления: 2018-04-15; просмотров: 148; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!


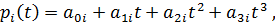
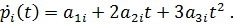

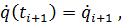
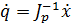 mit
mit