Представление выражений с помощью деревьев

⇐ ПредыдущаяСтр 12 из 37Следующая ⇒

С помощью деревьев можно представлять произвольные арифметические выражения. Каждому листу в таком дереве соответствует операнд, а каждому родительскому узлу √ операция. В общем случае дерево при этом может оказаться не бинарным.

Однако если число операндов любой операции будет меньше или равно двум, то дерево будет бинарным. Причем если все операции будут иметь два операнда, то дерево окажется строго бинарным.

Рис.. Представление арифметического выражения произвольного вида в виде дерева.

Рис. Представление арифметического выражения в виде бинарного дерева

Бинарные деревья могут быть использованы не только для представления выражений, но и для их вычисления. Для того чтобы выражение можно было вычислить, в листьях записываются значения операндов.

Затем от листьев к корню производится выполнение операций. В процессе выполнения в узел операции записывается результат ее выполнения. В конце вычислений в корень будет записано значение, которое и будет являться результатом вычисления выражения.

Помимо арифметических выражений с помощью деревьев можно представлять выражения других типов. Примером являются логические выражения. Поскольку функции алгебры логики определены над двумя или одним операндом, то дерево для представления логического выражения будет бинарным

Рис. Вычисление арифметического выражения с помощью бинарного дерева

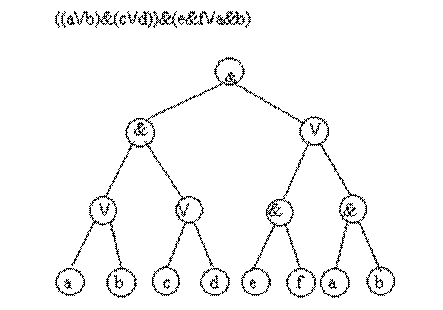
Рис. Представление логического выражения в виде бинарного дерева

Рассмотрим как связаны спрособы обхода дерева с различными формами записи выражения.Терминология способов охода дерева «префиксный», «инфиксный», «постфиксный» явно связана с обходом бинарного дерева, представляющего арифметическое выражение с бинарными операциями. Пусть, например, дано арифметическое выражение

(a + b) * c - d / (e + f * g) .

Соответствующее бинарное дерево.

Рис. Бинарное дерево, представляющее

арифметическое выражение (a + b) * c – d / (e + f * g)

Тогда три варианта обхода этого дерева порождают три известные формы записи арифметического выражения:

1) КЛП - префиксную запись

- * + a b c / d + e * f g ;

2) ЛКП - инфиксную запись (без скобок, необходимых для задания последовательности выполнения операций)

a + b * c - d / e + f * g ;

3) ЛПК - постфиксную запись

a b + c * d e f g * + / - .

ЛЕКЦИЯ 12. ГРАФЫ ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ. СПОСОБЫ ЗАДАНИЯ И РЕАЛИЗАЦИЯ

Цели и задачи лекции: показать способы задания и реализация графов

Основные рассматриваемые вопросы. Основные определения. Способы задания и реализация графов. Наличие циклов, связность.

Граф G - это упорядоченная пара (V, Е), где V- непустое множество вершин, Е - множество пар элементов множества V, называемое множеством ребер.

Упорядоченная пара элементов из V называется дугой. Если все пары в Е упорядочены, то граф называется ориентированным (орграфом).

Если дуга е ведет от вершины v_l к вершине v₂, то говорят, что дуга е инцидентна вершине v₂, а вершина v₂ являются смежной вершине v_v В случае неориентированного графа ребро е является инцидентной обеим вершинам v_l и v₂, а сами вершины - взаимно смежными.

Путь - это любая последовательность вершин орграфа такая, что в этой последовательности вершина в может следовать за вершиной а, только если существует дуга, следующая из а в в .

Путь, начинающийся и заканчивающийся в одной и той же вершине, называется циклом. Граф, в котором отсутствуют циклы, называется ациклическим.

Петля - дуга, соединяющая некоторую вершину сама с собой.

- Выбор структуры данных для хранения графа в памяти имеет принципиальное значение при разработке эффективных алгоритмов.

При дальнейшем изложении будем предполагать, что вершины графа обозначены символьной строкой и всего их до п, а ребер - до т. Каждое ребро и каждая вершина имеют вес - целое положительное число. Если граф не является помеченным, то считается, что вес равен единице.

Матрица смежности - это двумерный массив V, размером пХп:

При этом vij=0, если вершина i не смежна вершине; vij=весу ребра (дуги), если вершина i смежна вершине j, vij=весу петли.

Пространственная сложность этого способа V(n)~O(n²). Способ очень хорош, когда надо часто проверять смежность или находить вес ребра по двум заданным вершинам.

Матрица инцидентности — это двумерный массив U размером пХт:

При этом uij=0, если вершина i не инцидентна ребру j, uij=весу ребра, если вершина инцидентна ребру j.

Пространственная сложность этого способа V(n, m)~O(n*m). Матрица инцидентности лучше всего подходит для операции «перечисление ребер, инцидентных вершине х».

Списки смежных вершин - это одномерный массив размером п, содержащий для каждой вершины указатели на списки смежных с ней вершин:

type

PNode = ^ANode;

Node = record {смежная вершина}

Name: string; {имя смежной вершины}

Weight: integer; {вес ребра}
Next: PNode; {следующая смежная вершина}

end;

TAdjacencyList = array [l..n] of record
NodeWeight: integer; {вес вершины}
Name: string; {имя вершины}

List: PNode; {указатель на список смежных}

end; var

Graph: TAdjacencyList;

Пространственная сложность этого способа F_max(w)~0(w²). Хранение списков в динамической памяти позволяет сократить объем расходуемой памяти, так как в этом случае не будет резервироваться место под п соседей для каждой вершины. Можно и сам массив представить в виде динамического списка, но это не имеет особого смысла, так как граф обычно является статичной (неизменяемой) структурой.

Этот способ хранения лучше всех других подходит для операции «перечисление всех вершин, смежных с х».

Список ребер - это одномерный массив размером т, содержащий список пар вершин, инцидентных с одним ребром графа:

Пространственная сложность этого способа V(m)~O(m). Этот способ хранения графа особенно удобен, если главная операция, которой чаще всего выполняется, это перечисление ребер или нахождение вершин и ребер, находящихся в отношениях инцидентности.