Тема: «Вычисление определенных интегралов»
Цель работы: изучение методов вычисления определенных интегралов, оценка точности этих методов. Получение практических навыков программной реализации методов вычисления определенных интегралов.
Технические средства: IBM PS AT.
Программное средство: Visual Studio или Delphi
Теоретические сведения
Постановка задачи. Пусть некоторый конечный интервал [а, b] на оси Ох разбит на n подынтервалов [хi, хi+1], которые в дальнейшем будем называть элементарными отрезками. Ясно, что без ограничения общности можно положить х0 = а; хn= b и х0 < <х1 < ... <хn. Через hi обозначим длину элементарного отрезка (хi+1- хi). Если заданный отрезок [а, b] разбит равномерно, то тогда hi будет постоянна для любой 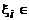 [а, b]. Пусть теперь на[а, b]определена некоторая функция f(х). Предположим, что необходимо найти приближение к определенному интегралу, которое обозначим
[а, b]. Пусть теперь на[а, b]определена некоторая функция f(х). Предположим, что необходимо найти приближение к определенному интегралу, которое обозначим 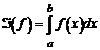 . Очевидно также, что если f(х) непрерывна
. Очевидно также, что если f(х) непрерывна  [а, b], то тогда
[а, b], то тогда 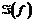 можно представить как
можно представить как 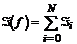 , где
, где 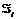 - интеграл функции f(х) на элементарном отрезке [хi+1, хi], т.е.:
- интеграл функции f(х) на элементарном отрезке [хi+1, хi], т.е.:
 .
.
Bсякая простая формула, аппроксимирующая отдельный интеграл  , назывaется квадратурной. Составная квадратурная формула - это формула, дающая приближение интеграла
, назывaется квадратурной. Составная квадратурная формула - это формула, дающая приближение интеграла 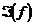 в виде суммы приближений интегралами
в виде суммы приближений интегралами 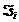 по данной квадратурной формуле.
по данной квадратурной формуле.
|
|
|
Двумя простейшими квадратурными формулами являются формулы прямоугольников и трапеций, которые в ряде случаев оказываются наиболее эффективными.
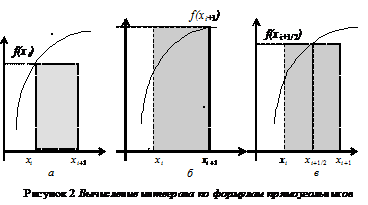
Известны три разновидности формул прямоугольников: это формулы левых, правых и средних прямоугольников. Все они основаны на аппроксимации каждого интеграла 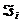 площадью прямоугольника, одной из сторон которого является hi , а второй - либо значение функции на левом конце отрезка (рис.2, а), либо значение функции на правом конце отрезка (рис. 2, б), либо значение функции в средней точке отрезка (рис. 2, в).
площадью прямоугольника, одной из сторон которого является hi , а второй - либо значение функции на левом конце отрезка (рис.2, а), либо значение функции на правом конце отрезка (рис. 2, б), либо значение функции в средней точке отрезка (рис. 2, в).
|
|
Квадратурные формулы, аппроксимирующие 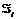 , будут иметь вид:
, будут иметь вид:
левых прямоугольников: 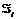 = hi f (хi);
= hi f (хi);
правых прямоугольников: 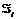 = hi f (хi+1);
= hi f (хi+1);
средних прямоугольников: 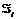 = hi f (хi+1/2).
= hi f (хi+1/2).
С учетом представления 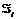 на элементарном отрезке составные квадpатурные формулы прямоугольников могут быть записаны так:
на элементарном отрезке составные квадpатурные формулы прямоугольников могут быть записаны так:
левых прямоугольников
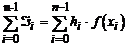 ; (3.1)
; (3.1)
правых прямоугольников
 ; (3.2)
; (3.2)
средних прямоугольников
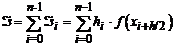 . (3.3)
. (3.3)
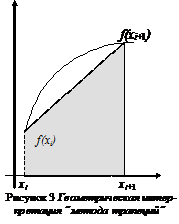
В формуле трапеций используются значения функции в концевых точках элементарных отрезков. В этом случае 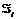 аппроксимируется площадью трапеции с основаниями f(хi) и f(хi+1)и высотой Dx (рис. 3).
аппроксимируется площадью трапеции с основаниями f(хi) и f(хi+1)и высотой Dx (рис. 3).
|
|
|
|
|
Тогда площадь фигуры моСт быть определена из формулы площади прямоугольной трапеции
Si = (fi + fi+1) hi /2.
Если теперь просуммируем последнюю формулу по всем элементарным отрезкам, то получим с учетом выполненных элементарных преобразований следующее выражение:
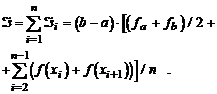
Заметим, что при бесконечном уменьшении длин элементарных отрезков формулы обоих типов (прямоугольников и трапеций) сходятся к точному значению интеграла 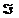 . Однако не ясно, как быстро они сходятся ? Попытаемся выяснить данный вопрос, воспользовавшись разложением функции в ряд Тейлора относительно центра элементарного отрезка [хi, хi+1]
. Однако не ясно, как быстро они сходятся ? Попытаемся выяснить данный вопрос, воспользовавшись разложением функции в ряд Тейлора относительно центра элементарного отрезка [хi, хi+1]
f(x) = f(yi) + (x – yi) f ’(yi) + (x – yi)2 f ’’(yi)/2 +
+ (x – yi)3 f’’’(yi)/6 + (x-yi)4 f (IV)(yi)/24 + …
затем, проинтегрировав полученный ряд по каждому из отрезков в предположении, что оставшиеся члены ряда намного меньше выписанных, с учетом значений коэффициентов ряда Тейлора на элементарном отрезке
|
|
|
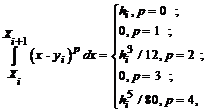
получим
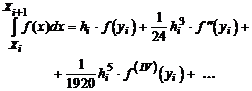
Член 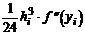 показывает ошибку формулы прямоугольников без учета членов более высокого порядС. Если теперь подставим в формулу трапеций значения функции в точках х = хi и х = хi+1, то получим
показывает ошибку формулы прямоугольников без учета членов более высокого порядС. Если теперь подставим в формулу трапеций значения функции в точках х = хi и х = хi+1, то получим

Можно видеть, что ошибки формул средних прямоугольников и трапеций одного порядС, т.е. дают почти одинаковую точность.
Формальные параметры процедуры вычисления интеграла методами прямоугольников и трапеций. Входные: Х0, Х1 (тип real) – границы отрезС, на котором вычисляется определенный интеграл; N (тип integer) – количество узлов (элементарных отрезков), на которые разбивается заданный интервал [a, b]. Выходные: FХ (тип real) – массив значений функции в заданных узлах (хi); fint (тип real) – вычисленные значения интеграла; err (тип real) – погрешность вычисленного значения.
Метод Симпсона часто называют в литературе методом парабол. Очевидно, что точность вычислений приближенного интеграла возрастет по сравнению с точностью вычислений, выполненных по формулами трапеций и прямоугольников, Сли подынтегральную функцию f(х) заменить на отрезке [хi,хi+1] квадратичной параболой, которая в узлах разбиения хi принимает значения f(хi) и при этом х0 = =а; f(х0) = f(а) = y0; хn = b; f(хn) = f(b) = yn .
|
|
|
Разобьем равномерно отрезок [а, b] на N элементарных отрезков [хi,хi+1] и на каждом из них заменим подынтегральную функцию f(х) интерполяционным многочленом Ньютона (или Лагранжа, в принципе, без разницы!) второй степени. Тогда для каждого элементарного отрезка [хi,хi+1] имеем следующее:
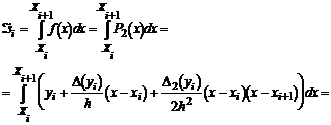
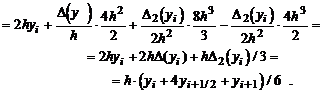
Просуммируем полученное выражение по всем элементарным отрезкам, и если подставим h = =(b - а) / n, то окончательно получим
 (3.4)
(3.4)
Данное выражение называется формулой Симсона. Онo относится к формулам повышенной точности и является точной для многочленов второй и третьей степени . Погрешность формулы Симсона оценивается по формуле Тейлора и имеет вид
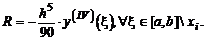
Интегрирование квадратурными формулами Ньютона - Котеса и методом "три восьмых".
Пусть некоторая функция f(х), как и раньше, задана в виде таблицы значений yi = f(хi)в узлах интерполяции хi = =х0+ ih на отрезке [а, b]. Требуется найти значения интеграла 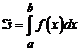 на указанном отрезке.
на указанном отрезке.
По заданным значениям подынтегральной функции yi = =f(хi) построим интерполяционный полином Лагранжа
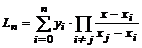 ,
,
который для равноотстоящих узлов примет вид
 ,
,
где q = (х - х0) / h.
Теперь заменим подынтегральную функцию f(х) построенным полиномом, считая, что узлы интерполяции расположены равномерно:
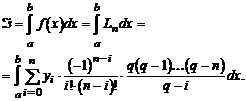
Проведя необходимые элементарные преобразования, выполнив замену переменных dq = dx/n и сменив в соответствии с подстановкой пределы интегрирования, получим

Здесь h - шаг, который для равноотстоящих узлов интерполяции определяется как h = (b - а)/n. Подставив значения h в последнюю формулу, окончательно получим
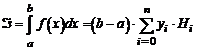 ,
,
где
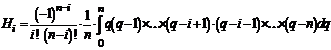 ;
;
Нi - коэффициенты Ньютона - Котеса. Они не зависят от значений функции f(х) и являются функциями только количества узлов, на которые разбит отрезок [а, b]. Поэтому Нi обычно вычисляют заранее:
N = 1: Н0 = Н1 = 1/2;
N = 2: Н0 = Н2 = 1/6; Н1 = 2/3;
N = 3: H0 = H3 = 1/8; H1 = H2 = 3/8;
N = 4: H0 = H4 = 7/90; H1 = H3 = 16/45; H2 = 2/13;
N = 5: H0 = H5 = 19/288; H1 = H4 = 25/96; H2 = H3 = 25/144.
Этот список при необходимости можно продолжить. Но если теперь рассмотреть частные случаи формулы Ньютона - Котеса, то:
1) при n = 1 получаем формулу трапеций:
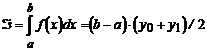 ;
;
1) при n = 2 получаем формулу Симсона:
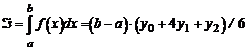 ;
;
2) при n = 3 получаем формулу "трех восьмых":
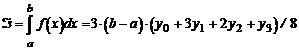 .
.
Погрешность последней формулы оценивается соотношением
R = -(3/80) h5 y(IV)(x)для всех x Î[a, b]\ xi .
Достроим таблицу коэффициентов до n = 7:
N = 6: H0 = H6 = 41/840; H1 = H5 = 9/35;
H2 = H4 = 9/280, Н5 = 34/105;
N = 7: H0 = H7 = 751/17280; H1 = H6 = 3577/17280;
H2 = H5 = 1323/17280; Н3 = Н4 = 2989/17280.
Задание
Написать программу для вычисления интегралов (методы задаются преподавателем).
Варианты
1. 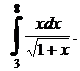 2.
2. 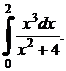 3.
3. 
4. 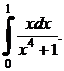 5.
5. 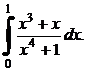 6.
6. 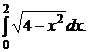
7. 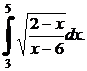 8.
8. 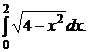 9.
9. 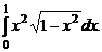
10. 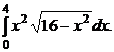
Требования к программе
1. Программа должна быть написана в среде Visual Studio или Delphi.
2. В программе должно быть предусмотрено следующее:
- ввод исходных данных и вывод результата в удобной для пользователя форме;
- возможность пошагового просмотра решения задачи;
- справка с комментариями по работе с программой;
- корректировка исходных данных;
- сохранение исходных данных и результата в файле.
Порядок выполнения работы
1. Получить задание у преподавателя.
2. Разработать алгоритм решения задачи.
3. Реализовать полученный алгоритм.
4. Проанализировать результаты работы алгоритма.
5. Оформить отчет по лабораторной работе.
Содержание отчета
1. Номер и тема лабораторной работы.
2. Цель выполнения работы.
3. Описание алгоритма.
4. Руководство пользователю.
5. Пример работы программы.
6. Анализ полученных результатов и вывод по работе.
7. Текст программы с комментариями привести в приложении.
Лабораторная работа № 4
Дата добавления: 2018-04-15; просмотров: 545; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!