Разработать программное средство для решения систем линейных уравнений (методы решения определяет преподаватель).
Лабораторная работа № 1
Тема: «Прямые и итерационные методы решения систем линейных уравнений»
Цель работы: изучение методов решения линейных уравнений, оценка и сравнение этих методов. Получение практических навыков программной реализации методов решения систем линейных уравнений.
Технические средства: IBM PS AT.
Программное средство: Delphi или Visual Studio
Теоретические сведения
Система m линейных алгебраических уравнений с n неизвестными в общем виде может быть записана следующим образом:
 (1.1)
(1.1)
или в матричном виде AX = B, где A - прямоугольная матрица размерности m´n, X - вектор n-го порядка, B- вектор m-го порядка. Решением системы (1) называется такая упорядоченная совокупность чисел 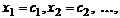
 которая обращает все уравнения системы в верные равенства. Две системы называются эквивалентными (равносильными), если множества их решений совпадают.
которая обращает все уравнения системы в верные равенства. Две системы называются эквивалентными (равносильными), если множества их решений совпадают.
Система линейных уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной - в противном случае. Совместная система называется определенной, если она имеет единственное решение, и неопределенной - в противном случае. Система является определенной, если rang A = rang B, где матрица B, полученная из матрицы A добавлением столбца свободных членов, называется расширенной.
|
|
|
Если матрица A- квадратная и det A ¹ 0, то она называется неособенной (невырожденной), при этом система уравнений, имеющая неособенную матрицу A, совместна и имеет единственное решение.
Eсли уравнения (1) являются нелинейными относительно неизвестного вектора Х, то соответствующая система, записанная в векторной форме
 (1.2)
(1.2)
называется системой нелинейных уравнений. Она может быть также представлена в координатном виде:
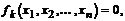 1 < k < n.
1 < k < n.
Многообразие численных методов решения систем линейных алгебраических уравнений можно разделить на два класса: прямые (или точные) и итерационные (или приближенные) методы. В лабораторной работе рассматриваются эффективные алгоритмы, реализующие ряд методов из обоих классов.
Метод исключения Гаусса для систем линейных уравнений
Из курса линейной алгебры известно, что решение системы линейных уравнений можно просто найти по правилу Крамера - через отношение определителей. Но этот способ не очень удобен для решения систем уравнений с числом неизвестных > 5, т.е. когда найти определитель сложно, а при числе неизвестных > 10 нахождение определителя с достаточно высокой степенью точности становится самостоятельной вычислительной задачей. В этих случаях применяют иные методы решения, среди которых самым распространенным является метод Гаусса.
|
|
|
Запишем систему линейных уравнений (1.1) в виде
 (1.3)
(1.3)
Если матрица системы верхняя треугольная, т.е. ее элементы ниже главной диагонали равны нулю, то все хj можно найти последовательно, начиная с хn, по формуле
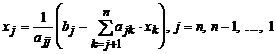 . (1.4)
. (1.4)
При j > k и аjj ¹ 0 этот метод дает возможность найти решение системы.
Метод Гаусса для произвольной системы (1.1) основан на приведении матрицы Асистемы к верхней или нижней треугольной. Для этого вычитают из второго уравнения системы первое, умноженное на такое число, при котором а21 = 0, т.е. коэффициент при х1 во второй строке должен быть равен нулю. Затем таким же образом исключают последовательно а31 , а41 , ..., аm1 . После завершения вычислений все элементы первого столбца, кроме а11, будут равны нулю.
|
|
|
Продолжая этот процесс, исключают из матрицы А все коэффициенты аij, лежащие ниже главной диагонали.
Построим общие формулы этого процесса. Пусть исключены коэффициенты из k - 1 столбца. Тогда ниже главной диагонали должны остаться уравнения с ненулевыми элементами:
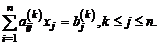
Умножим k-ю строку на число
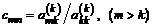
и вычтем ее из m-й строки. Первый ненулевой элемент этой строки обратится в нуль, а остальные изменятся по формулам
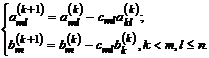 (1.5)
(1.5)
Произведя вычисления по формулам (1.5) при всех указанных индексах, исключим элементы k-го столбца. Такое исключение назовем циклом, а выполнение всех циклов назовем прямым ходом исключения.
После выполнения всех циклов получим верхнюю треугольную матрицу А системы (1.3), которая легко решается обратным ходом по формулам (1.4). Если при прямом ходе коэффициент аjj оказался равен нулю, то перестановкой строк перемещаем на главную диагональ ненулевой элемент и продолжаем расчет.
Формальные параметры процедуры. Входные: n (тип integer) - порядок системы; а (тип real) - массив коэффициентов системы размером n´n; b (тип real) - массив-строка свободных членов. Выходные: х (тип real) - массив-строка, в который помещается решение системы.
|
|
|
Метод главных элементов
На практике применяют множество вариантов вычислительных схем метода Гаусса. Например, при приведении матрицы к верхней треугольной форме выбирают наибольший элемент (в строке или столбце), уменьшая вычислительную погрешность за счет деления на не самый маленький элемент. Такая вычислительная схема называется методом Гаусса с выбором ведущего элемента. Если же выбирать при приведении матрицы самый большой (по модулю) элемент из всех оставшихся, то такая схема будет называться методом Гаусса с выбором главного элемента. Последняя схема относится к наиболее популярным. Главное ее отличие от метода Гаусса состоит в том, что при приведении матрицы А к верхней (или нижней) треугольной форме ее строки и столбцы переставляют так, чтобы наибольший из всех оставшихся элементов матрицы стал ведущим, и на него выполняется деление. Если матрица хорошо обусловлена, то в методе Гаусса с выбором главного элемента погрешности округления невелики.
Формальные параметры процедуры. Входные: n (тип integer) - целое положительное число, равное порядку исходной системы; aa (тип real) - массив из n´n действительных чисел, содержащий матрицу коэффициентов системы (aa[1] = а11; aa[2] = а21; aa[3] = a31; ...; aa[n]= an1; aa[n +1]= =a12; aa[n + 2] = a22; ...; aa[2*n] = аn2; ...; aa[n*n] = аnn); b (тип real) - массив из n действительных чисел, содержащий столбец свободных членов исходной системы (b[1] = =b1; b[2] = b2; ...; b[n] = bn). Выходные: b (тип real) - массив из n действительных чисел (он же был входным) при выходе из подпрограммы, содержащий решения исходной системы (b[1]= x1; b[2] = x2; ...; b[n] = xn); ks (тип integer) - признак правильности решения или код ошибки: если ks = 0, то в массиве b содержится решение исходной системы; если ks = 1, то исходная система не имеет решения (главный определитель ее равен нулю).
Решение систем линейных уравнений методом итераций
Итерационные методы решения систем линейных уравнений дают возможность вычислить решение системы как предел бесконечной последовательности промежуточных решений. Причем каждое последующее решение в случае сходимости итерационного процесса считается более точным. В этих методах, в отличие от точных, ошибки в начальном приближении и последующих вычислениях компенсируются, т.е. итерационные методы (в случае сходимости) позволяют получить решение более точное, чем прямые. Поэтому итерационные методы относят к самоисправляющимся.
Условия и скорость сходимости процесса в большей степени зависят от свойств уравнений, т.е. от свойств матрицы системы и от выбора начального приближения.
Пусть дана система линейных алгебраических уравнений (1)с неособенной матрицей. В методе простой итерации если аii ¹ 0, то исходная система может быть преобразована к виду хi = bi + aij хj , i ¹ j, т.е. из каждого уравнения последовательно выражают хi.
Здесь bi = Fi / аii; aij = - аij / аii. Таким образом, в матричном виде имеем Х = В+ AХ. Полученную систему будем решать методом последовательных приближений. За нулевое приближение Х(0)можно принять матрицу В:Х(0)= = B, и далее, подставив найденные значения в исходную систему, получим Х (1) = В + A Х(0) .
При бесконечном повторении этой вычислительной схемы имеем
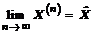 ,
,
где 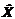 и будет искомое решение системы.
и будет искомое решение системы.
Условия сходимости итерационного процесса определяются теоремами, которые приводятся нами без доказательств.
Теорема 1. Для того, чтобы последовательность приближений Х(n) сходилась, достаточно, чтобы все собственные значения матрицы A были по модулю меньше единицы: | li | < 1, i = 1, 2, ..., n.
Теорема 2. Если требовать, чтобы последовательность Х(n) сходилась к 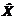 при любом начальном приближении Х(0) , то условие теоремы 1 является необходимым.
при любом начальном приближении Х(0) , то условие теоремы 1 является необходимым.
Применение теорем 1 и 2 требует знания всех собственных значений матрицы A, нахождение которых является очень не простой задачей. Поэтому на практике ограничиваются более простой теоремой, дающей достаточные условия сходимости.
Теорема 3. Если для системы Х= В+ AХ выполняется хотя бы одно из условий :
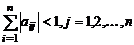 ;
;
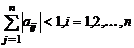 ,
,
то итерационный процесс сходится к единственному решению этой системы независимо от выбора начального приближения.
Для многих приложений важно знать, какой является скорость сходимости процесса, и оценить погрешность полученного решения.
Теорема 4. Если какая-либо норма матрицы A, согласованная с рассматриваемой нормой вектора Х, меньше единицы, то верна следующая оценка погрешности приближения в методе простой итерации:
 .
.
Формальные параметры процедуры. Входные: А (тип real) - матрица, составленная из коэффициентов при Х преобразованного уравнения; В (тип real) - матрица, составленная из свободных членов; N (тип integer) - размерность матриц А(N ´ N) и В(N); IK (тип integer) - предельно возможное количество итераций (введено для того, чтобы в случае расхождения процесса выйти из подпрограммы. Обычно решение достигается за 3-6 итераций); ЕРS (тип real) - заданная погрешность решения. Выходные: Х(тип real) - матрица, в которой находится решение системы.
Решение систем линейных уравнений методом Зейделя
Этот метод относится к итерационным, имеет более быструю сходимость по сравнению с методом простых итераций .
Метод Зейделя применяют в двух расчетных схемах. Рассмотрим каноническую форму (для схемы итераций). Пусть система приведена к виду Х = Вх + b. В схеме простой итерации следующее приближение Х(k +1) находится путем подстановки предыдущего приближения Х(k) в правую часть выражения X(k +1) = B X (k) + b.
Для удобства рассуждений полагаем, что левые части уравнений содержат хi (элементы матрицы X(k +1)) с возрастающими номерами, т.е. сначала х1, затем х2, х3, ..., хn. Тогда решение системы уравнений Х = Вх +b на очередной (k +1) итерации будет имет вид
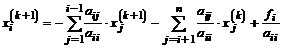 , (1.6)
, (1.6)
т.е. каждое очередное найденное приближение хi(k +1)сразу же используется для определения 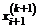 . Условия сходимости для итерационного метода Зейделя дают те же теоремы, что и в методе простых итераций.
. Условия сходимости для итерационного метода Зейделя дают те же теоремы, что и в методе простых итераций.
Вторая форма метода Зейделя требует предварительного приведения системы (1) к виду, когда все диагональные элементы отличны от нуля. Если разложить матрицу А на сумму двух матриц R + С, где R - нижняя диагональная матрица, а С- верхняя с нулями на главной диагонали, то систему (1) можно записать как
Ax = (R + C)x = R x(k +1) + C x(k) = B
или x(k +1) = R-1B - R-1C x(k)
и тогда становится ясно, что метод Зейделя в канонической форме равносилен методу простой итерации, примененному к системе
X = R-1B - R-1C X.
Формальные параметры процедурытакие же, как и в методе итераций.
Задание
Разработать программное средство для решения систем линейных уравнений (методы решения определяет преподаватель).
Варианты
1. 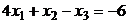 2.
2. 
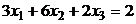
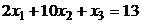
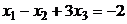 .
. 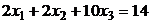 .
.
3. 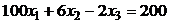

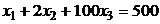 .
.
4. 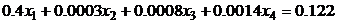
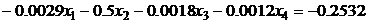


5. 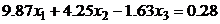
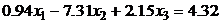
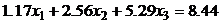 .
.
6. 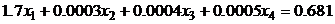
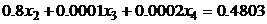
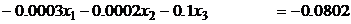
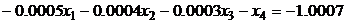
7. 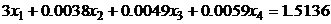
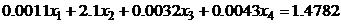


8. 
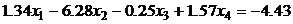
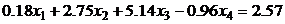
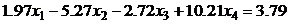
9. 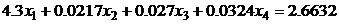

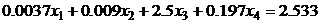

10. 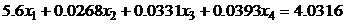
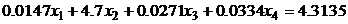
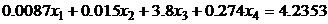
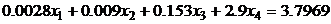
Требования к программе
1. Программа должна быть написана в среде Visual Studio или Delphi.
2. В программе должно быть предусмотрено следующее:
- ввод исходных данных и вывод результата в удобной для пользователя форме;
- возможность пошагового просмотра решения задачи;
- справка с комментариями по работе с программой;
- корректировка исходных данных;
- сохранение исходных данных и результата в файле.
Порядок выполнения работы
1. Получить задание у преподавателя.
2. Разработать алгоритм решения задачи.
3. Реализовать полученный алгоритм.
4. Проанализировать результаты работы алгоритма.
5. Оформить отчет по лабораторной работе.
Содержание отчета
1. Номер и тема лабораторной работы.
2. Цель выполнения работы.
3. Описание алгоритма.
4. Руководство пользователю.
5. Пример работы программы.
6. Анализ полученных результатов и вывод по работе.
7. Текст программы с комментариями привести в приложении.
Лабораторная работа № 2
Тема: «Интерполирование и экстраполирование функций»
Цель работы: изучение методов интерполирования и экстраполирования функции. Получение практических навыков программной реализации методов интерполирования и экстраполирования функции.
Технические средства: IBM PS AT.
Программное средство: Visual Studio.
Теоретические сведения
Предположим, что задано некоторое упорядоченное множество вещественных абcцисс х1, х2, ..., хn и связанное с ним множество вещественных ординат у1, у2, ..., уn. Пусть х1< х2< ...< хn и каждое уi есть некоторое вещественное число, отвечающее хi, которое определяется математически или в результате каких-либо наблюдений (рис. 2.1). Точки (xi,yi)называются узлами интерполяции. Кривая, которая точно проходит через эти узлы, называется интерполяционной кривой.
|
|
При решении задач на ЭВМ достаточно часто возникает обратная задача, т.е. необходимо подобрать некоторую простую функцию, которая, с одной стороны, имела бы в известных точках заданные значения, а с другой — вычислялась бы быстрee и проще исходной.
Исходя из изложенного можно сформулировать (не строго) следующие определения. Задача одномерной интерполяции заключается в построении такой непрерывной функции f, при которой f(хi)º уi для всех хi, т.е. функция f обязательно должна проходить абсолютно точно через заданные узлы интерполяции. Однако при этом f(xk) должна принимать "разумные" значения для всех xk, лежащих между заданными точками хi. Кроме того, на интерполирующую функцию накладывается еще ряд очевидных ограничений: не иметь особых точек на интервале интерполирования; быть достаточно гладкой; иметь необходимое количество производных и пр. Если функция определена и непрерывна на [y1, y2],ее интерполяционные узлы расположены на [х1, х2], а точка x Ï [х1, х2] или f(x)Ï [y1, y2],то тогда говорят о задаче экстраполирования функции.
Таким образом, задачи интерполирования и экстраполирования возникают в следующих случаях:
1) если решаются прогнозные задачи (экстраполирование);
2) практически всегда при решении различных практических задач (интерполирование и экстраполирование);
3) при обработке данных, полученных в экспериментах (интерполирование);
4) всегда при решении задач на ЭВМ (интерполирование и экстраполирование);
5) при задании функции графиком или таблицей (интерполирование и экстраполирование);
6) во всех остальных не описанных здесь случаях, если это необходимо.
Построение интерполяционного полинома Лагранжа по заданным значениям функции
Пусть теперь функция f(x)известна лишь в х1, х2, ..., хn узлах некоторой сетки. Попытаемся построить такую другую функцию j(х;a), которая полностью совпадала бы с заданной f(x)в этих узлах, т.е. j(х; a) = j(х, а1, а2, ..., ат)ººf(xк). Тогда из последнего равенства можно будет определить компоненты a. При k £ т, а в частном случае k = т, компоненты aопределяются из решения системы
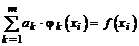 , (*)
, (*)
которая в указанных случаях имеет единственное решение, если ее главный определитель отличен от нуля:

 .
.
Система функций, удовлетворяющая условию (*), является Чебышевской.
Одним из самых важных классов среди интерполирующих функций является множество алгебраических полиномов вида
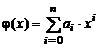 ,
,
где аi - некоторые неизвестные коэффициенты. Для того чтобы их определить однозначно, необходимо иметь n+1 точек для построения системы из n линейных уравнений относительно аi:
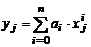 , (j = 0, 1, ..., N+1).
, (j = 0, 1, ..., N+1).
При этом потребуем, чтобы построенный полином в заданных узлах хi Î {Х} в точности совпадал со значениями f(хi) в указанных точках. Если среди множества хi нет совпадающих, тогда система линейных уравнений, полученная относительно аi,
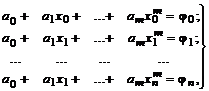
определена, имеет решение и это решение единственное. Заметим, что главный определитель системы - это определитель Вандермонда:
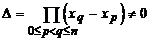 ,
,
который при выполнении названных условий всегда отличен от 0. Значит система имеет решение и это решение будет единственное. Очевидно, что решением системы будет полином n-й степени, который называют полиномом Лагранжа и записывают
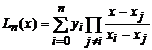 . (2.1)
. (2.1)
Важно отметить, что существует один и только один полином степени меньше n, который интерполирует заданные n + 1 точки. При использовании всего известного набора точек интерполирующий полином называют глобальным интерполирующим полиномом. Однако по теореме Фабера при специальном расположении узлов интерполяции n всегда можно найти такой полином Рn, непрерывный на заданном отрезке [х0, хn], который не сходится к f, несмотря на то, что Рn(хi)º уi . Поэтому на практике редко пользуются глобальным интерполирующим полиномом, заменяя его полиномом степени не выше 5. Тогда говорят о скользящей интерполяции.
Формальные параметры процедуры. Входные: b (тип real) - точка на оси Ох, для которой ищутся значение функции; n (тип integer) - количество точек, по которым строится интерполирующий полином. Степень полинома должна быть на единицу меньше n; x, y (тип real) - массивы, в которых находятся заданные значения точек. Выходные: L (тип real) - значение функции в точке b.
При большом количестве точек n могут оказаться решающими ошибки, связанные с округлением при вычислении высших степеней х, что приведет к расхождению решения. Кроме того, ошибки округления накапливаются на каждом очередном шаге, поэтому оценка ошибки интерполирования должна обязательно вычисляться в каждом конкретном случае на каждом расчетном шаге.
Один из возможных способов оценки ошибки при интерполировании заключается в следующем. Во-первых, предполагают, что заданные числа уi являются в действительности значениями некоторой функции f(хi). Во-вторых, что f(хi) имеет n +1 непрерывную производную для всех хi. В-третьих, что Pn - единственный полином степени < n, интерполирующий заданные точки {(хi , уi)}. Тогда можно доказать, что для любого действительного хi выполняется
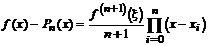 ,
,
где x - некоторая неизвестная точка на интервале, определяемом точками х0, х1, ..., хn и хn+1. Когда известны границы для f(х), эта разность дает оценку ошибки.
Построение интерполяционного полинома Ньютона по заданным значениям функции
В силу единственности многочлена степени n, построенного по n + 1 значениям функции f(х), многочлен Ньютона Рn(х) является разновидностью записи интерполяционного многочлена и полностью совпадает с многочленом, построенным по формуле Лагранжа (2.1). Однако с помощью многочлена Ньютона удобнее проводить интерполяцию в начале и конце таблицы значений функции.
В начале таблицы используют первую интерполяционную формулу Ньютона, а в конце - вторую. Рассмотрим один из способов построения первой интерполяционной формулы.
Пусть некоторая функция f(х) задана табличными значениями у0 = f(х0); у1= f(х1); ...; уn = f(хn) в равноотстоящих узлах интерполяции {х0 , х1 = х0 + h;...; хn = x0+ nh}. Требуется построить интерполяционный полином Ньютона Рn(х)степени n, при котором
Рn(х0)º у0; Рn(х1)º у1; ...; Рn(хn)º уn . (2.2)
Будем искать полином в виде
Pn(x0) = a0 + a1(x - x0) +a2(x - x0) (x - x1) + ...
...+ an(x - x0) (x - x1)...(x - xn), (2.3)
где неизвестные коэффициенты аi находятся из очень простых зависимостей. Для того чтобы найти а0, положим х=х0. Очевидно, что при этом Рn(х0) º у0 а0 [это следует из формулы (2.2) ]. Но так как все члены уравнения (2.3) , кроме первого, содержат сомножитель (x - x0), следовательно, они все станут равными нулю, и из формулы (2.3) с учетом формулы (2.2) имеем Рn(х0) = а0 º у0 .
Для того чтобы найти а1, положим х = х1. Повторив все рассуждения и учитывая, что значение полинома в указанной точке будет тождественно равно у1 [формула (2.2)], после подстановки в формулу (2.3) х1 имеем
Pn(x1) = a0 + a1(x1 - x0) = у0 + а1 h = у1 .
Все остальные сомножители при неизвестных коэффициентах аi будут равны нулю. Преобразуя последнее выражение, находим а1 как а1 = D1/h [здесь D1 = Рn(х0 + h) - -Рn(х0) = у1 - у0 ].
Для того чтобы определить а2, положим х = х2 и, рассуждая аналогично, определим третий коэффициент как a2 = D2 / (2! h2).
Подставляя в выражение (2.3) последовательно все хn, приходим к общей формуле для получения коэффициентов аi:
ai = Di / ( i! hi),
которые подставим в формулу (2.3) и получим первую интерполяционную формулу Ньютона:
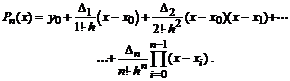 (2.4)
(2.4)
В формуле (2.4) обычно выполняют замену переменных: q = (х - х0)/h, где h - шаг интерполирования. Тогда первая интерполяционная формула Ньютона записывается несколько иначе:
 (2.5)
(2.5)
При n = 1 получаем формулу линейного интерполирования; при n = 2 - параболического интерполирования и т.д.
Вторую интерполяционную формулу Ньютона получают, если узлы интерполяции в Рn(х) берут в несколько ином порядке:
Pn(x0) = a0 + a1(x - xn) + a2(x - xn) (x - xn-1) + ...
...+ an(x - xn) (x - xn-1) ... (x - x0) .
Тогда, рассуждая как и в случае первой интерполяционной формулы, получаем искомую форму записи полинома Ньютона, которая известна как вторая интерполяционная формула:
 (2.6)
(2.6)
Выполнив подстановку q = (х - хn)/h, получим иную запись интерполяционого многочлена Ньютона:
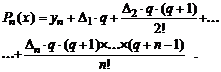 (2.7)
(2.7)
Первая интерполяционная формула Ньютона используется для интерполирования в начале отрезка [хi, хi+1] и эктраполирования до первой точки х0, т.е. для интерполирования вперед и экстраполирования назад. При таком интерполировании q = (х - хi)/h > 0. При экстраполировании назад по первой интерполяционной формуле q = (х - хi)/h < 0. При интерполировании в конце таблицы, т.е. при интерполировании назад, когда шаг интерполяции постоянен, применяют вторую интерполяционную формулу Ньютона, где q = (х - хi+1) / h < 0. Эту же формулу используют при экстраполировании вперед (в конце таблицы), но тогда q = (х - -хi+1)/ h>0.
Как уже отмечалось, полином Ньютона является иной записью полинома Лагранжа для функции, заданной в равноотстоящих узлах интерполяции.
Формальные параметры процедур. Входные: x, y (тип real) - массивы заданных значений хi и yi; n (тип integer) - количество точек в массивах x и y; x1 (тип real)- искомая точка. Выходные: процедура-функция возвращает вещественное значение функции в точке х1 согласно построенному полиному.
Оценка погрешности первой и второй интерполяционных формул Ньютона получается из оценки погрешности интерполяционного полинома Лагранжа. Введем обозначение h = хi+1 - хi и полагая для первой интерполяционной формулы q = (х - х0)/h, а для второй q = (х - хn)/h, получим для первой интерполяционной формулы
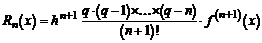
и для второй интерполяционной формулы
 .
.
Здесь x - некоторая точка из отрезка интерполирования [х0, хn] в случае задачи интерполирования или не принадлежащая указанному отрезку в случае задачи экстраполирования. Выполняя предельный переход для
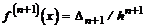
и подставляя последнее выражение в формулу для погрешности, окончательно будем иметь для первой интерполяционной формулы

и для второй интерполяционной формулы
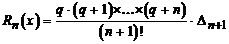 .
.
По последним формулам производится оценка погрешности интерполирования.
Интерполяция функции кубическими сплайнами
На практике редко проводят интерполяцию полиномами высших степеней, так как, во-первых, они дают значительные погрешности и, во-вторых, при бесконечном увеличении порядка n интерполяционного полинома Рn(х) последовательность Pn расходится (согласно теореме Фабера). Этот факт впервые обнаружил Рунге в 1901 г. Им же была высказана идея об интерполировании движущимися полиномами. Однако, так как сплайн-интерполяция давала более хорошие и устойчивые результаты, эта идея не получила широкого распространения.
Haибольшей популярностью сегодня на практике при интерполяции пользуются полиномы 2-й и 3-й степени. Остановимся подробнее на полиномах 3-й степени, так называемых кубических сплайнах.
Кубические сплайн-функции моделируют очень старое механическое устройство, которым пользовались чертежники. Они брали гибкие рейки, изготовленные из достаточно упругого материала, например из дерева. Эти рейки закрепляли, подвешивая грузики в точках интерполяции, называемых интерполяционными узлами. Рейка или механический сплайн принимали форму с наименьшей потенциальной энергией. Последнее условие имеет свое математическое выражение: f(IV)(x)º 0. Если при этом сплайн н е разрушается, то тогда следует, что f и f' должны быть непрерывны на[х0, хn] . Из теории балок известно, что функция f(х) между каждой парой заданных точек может быть предствлена полиномом 3-й степени
f(xi) = ai + bi(x - xi) + ci(x - xi)2 + di(x - xi)3,
где хi-1< х < хi. При этом между каждой парой соседних узлов полиномы соединяются непрерывно (так же, как их первые и вторые производные).
Кубическую сплайн-функцию, удовлетворяющую условиям f"(х1) = f"(хn )= 0, называют естественным кубическим сплайном. С математической точки зрения было доказано [Алберг, 1972], что она является единственной функцией, обладающей минимальной кривизной среди всех функций, интерполирующих данные точки и имеющих квадратично интегрируемую вторую производную. В этом смысле кубический сплайн будет самой гладкой функцией, интерполирующей заданные точки.
Построение кубического сплайна - простой и численно устойчивый процесс. Вычислительных схем, реализующих построение кубического сплайна по заданным значениям функции, в математике известно довольно много. Здесь нами рассмотрена одна из эффективных и простых вычислительных схем, обладающая свойством абсолютной устойчивости. Рассмотрим подинтервал [хi, хi+1] и пусть
hi = хi+1 - хi; w = (х - хi )/ h ; W = 1 - w.
Очевидно, когда х пробегает значения из указанного подинтервала, w изменяется от 1 до 0, а W - от 0 до 1. Рассуждая, приходим к следующему представлению сплайна на этом подинтервале:
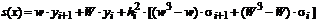 ,
,
где si и si+1 - некоторые константы, которые предстоит определить.
Первый и второй члены в этой формуле соответствуют линейной интерполяции, а член, взятый в квадратные скобки,- это кубическая поправка, которая обеспечивает необходимую гладкость функции. Отметим, что она на концах подынтервала обращается в 0 и тогда s(хi) = уi; s(хi+1) = уi+1. Таким образом, s(х) будет интерполировать заданные значения независимо от выбораsi
Продифференцируем трижды s(х) как сложную функцию от х и, учитывая, что w' = 1/hi, W' = -1/hi, получим производные s(х) 1-, 2- и 3-го порядков
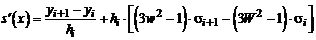 ,
,
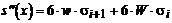 ,
, 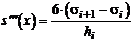 . Заметим, что s"(х) - линейная функция, интерполирующая значения6si и6si + 1 в точке х = хi . Следовательно, коэффициент si = s"(хi)/6, а s'''(х) является константой на каждом подинтервале и поэтому четвертая производная тождественно равна 0.
. Заметим, что s"(х) - линейная функция, интерполирующая значения6si и6si + 1 в точке х = хi . Следовательно, коэффициент si = s"(хi)/6, а s'''(х) является константой на каждом подинтервале и поэтому четвертая производная тождественно равна 0.
На концах подинтервала s'+(хi) = s'-(хi), так как ранее было выставлено требование непрерывности функции s(х). Но, с другой стороны,
s'+(хi) = Di - hi (si+1 +2si) и s'-(хi+1) = Di + hi (2si+1+si),
где Di = (уi+1 - уi)/hi. С учетом равенства производных слева и справа в окрестности каждой точки для всех i получаем
Di - hi(si+1+ 2si) = Di-1 - hi-1(2si + si-1),
откуда имеем трехточечную систему из n - 2 линейных уравнений относительно si
hi-1si-1+ 2(hi-1+ hi)si + hi si+1 = Di - Di-1,
где i = 1, 2, ..., n.
Заменим третью производную по s разностью третьего порядка. Тогда условие для s'''(х) в краевых точках i =1 и i = n запишется
(s2- s1) / h1 = D1(3)(sn - sn-1) / hn-1 = D(3)n-3.
Здесь введены следующие обозначения:
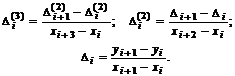
Умножим полученные равенства для разностей третьего порядка на квадрат их знаменателей и получим:
-h1s1 + h1s2 = h12D1(3) ; hn-1sn - hn-1sn-1= -hn-12D(3)n-3 .
Таким образом, для сплайна с заданными выше граничными условиями коэффициенты si удовлетворяют следующей системе из n линейных уравнений с n неизвестными:
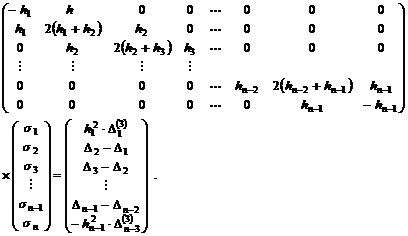
Последнюю систему из n линейных уравнений с n неизвестными можно решать методом исключения, но однако если при решении использовать особые свойства матрицы системы (она трехдиагональная, симметричная, для любого выбора х1< х2< ... < хn невырожденная и диагонально доминирующая), то всегда существует единственное решение системы. Обозначим это решение через s1, s2, ..., sn . Можно также показать, поскольку для всех х1, х2, ..., хn матрица коэффициентов хорошо обусловлена, то Гауссово исключение приведет исходную систему к ленточной форме:
 .
.
Здесь вычисляются
- диагональные элементы ai:
a1 = - h1 ;ai = 2(h i-1 + hi) - h2i-1 / ai-1 ;
an = -hn-1 - h2n-1/ an-1;
- правые части матрицы bi:
b1 = h21 D(3)1; bi = (Di - Di-1) - hi-1bi-1 / ai-1;
bn = -h2n-1D(3)n-3- hn-1bn-1/ an-1,
(здесь для всех соотношений i = 2, 3, ..., n-1). Тогда искомые si определяются через обратную подстановку
sn = bn / an; si = (bi - hi s i+1) / a i
для всех i = n - 1, n - 2, ..., 1.
Вычислительные схемы, используемые для решения систем с трехдиагональной матрицей, традиционно называют методом прогонки.
В некоторых случаях по различным причинам предпочтительнее вычислять и сохранять коэффициенты bi, сi и di для функции s(х), записанной в несколько ином виде :
s(х) = уi + bi (х - хi ) + сi (х - хi)2 + di (х - хi )3 ,
x Î [xi, xi+1],
где на каждом подынтервале [хi, хi+1] указанные коэффициенты выражаются через s i и hi:
bi = (уi+1- уi) / hi - hi (si+1 + 2si); сi = 3si;
di = (si+1 - si) / hi.
Использованиe такой формы хранения сплайнов упрощает некоторые операции с ними, например при вычислении производных и интегралов. Заметим попутно, что при N = 1 сплайн совпадает с многочленом Ньютона первой степени.
На практике, если дано достаточно много точек, то для построения кубического сплайна выбирают 4 последовательно расположенные, по которым строят первый полином. Затем сдвигаются на 3 точки и снова по 4 последовательным точкам строят следующий сплайн. И так поступают до тех пор, пока все точки не будут выбраны.
Формальные параметры процедур. Входные: n (тип integer) - количество точек, по которым строится сплайн (oно должно быть не меньше 2, но не больше 4); x, y (тип real) - два массива размером 1´n, в которые предварительно записаны данные для построения очередного сплайна. Выходные: b, c, d (тип real) - массивы коэффициентов кубического сплайна, если были предложены 4 точки.
Задание
По заданному преподавателем методу разработать программное средство.
Требования к программе
1. Программа должна быть написана в среде Visual Studio или Delphi.
2. В программе должно быть предусмотрено следующее:
- ввод исходных данных и вывод результата в удобной для пользователя форме;
- справка с комментариями по работе с программой;
- корректировка исходных данных;
- сохранение исходных данных и результата в файле.
Порядок выполнения работы
1. Получить задание у преподавателя.
2. Разработать алгоритм решения задачи.
3. Реализовать полученный алгоритм.
4. Проанализировать результаты работы алгоритма.
5. Оформить отчет по лабораторной работе.
Содержание отчета
1. Номер и тема лабораторной работы.
2. Цель выполнения работы.
3. Описание алгоритма.
4. Руководство пользователю.
5. Пример работы программы.
6. Анализ полученных результатов и вывод по работе.
7. Текст программы с комментариями привести в приложении.
Лабораторная работа № 3
Дата добавления: 2018-04-15; просмотров: 250; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

