Бесконечно - малые последовательности
Определение 1. Последовательность 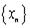 называется бесконечно-малой последовательностью, если
называется бесконечно-малой последовательностью, если 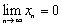 , т.е. если
, т.е. если
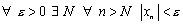 .
.
Определение 2. Последовательность 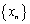 называется бесконечно-большой последовательностью, если
называется бесконечно-большой последовательностью, если 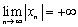 (это записывается еще и так:
(это записывается еще и так:  , не учитывая знака перед
, не учитывая знака перед 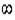 ), т.е. если
), т.е. если
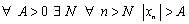 .Изучим некоторые свойства этих последовательностей.
.Изучим некоторые свойства этих последовательностей.
10. Сумма и разность бесконечно-малых последовательностей есть также бесконечно-малая последовательность.
Доказательство:
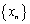 - б.м.п. =>
- б.м.п. =>
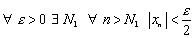
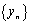 - б.м.п. =>
- б.м.п. =>

Возьмем 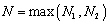 . Тогда
. Тогда
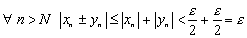
откуда следует, что 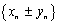 есть б.м.п.
есть б.м.п.
Следствие. Сумма любого конечного числа б.м.п. ест также б.м.п
20. Произведение б.м.п на ограниченную последовательность есть б.м.п.
Доказательство:
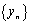 - ограничена. =>
- ограничена. =>
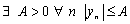
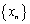 - б.м.п. =>
- б.м.п. =>
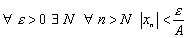 .
.
Но тогда 
отсюда и следует, что  есть б.м.п.
есть б.м.п.
3. Б.м.п. ограничена
Доказательство:
Пусть 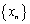 - б.м.п. Тогда
- б.м.п. Тогда 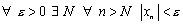 .
.
Возьмем  .
.
Тогда  т.е.
т.е. 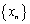 ограничена.
ограничена.
Следствие. Произведение б.м.п. есть также б.м.п.
4. Пусть 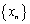 - б.м.п. и
- б.м.п. и 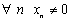 . Тогда
. Тогда 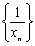 есть б.б.п.
есть б.б.п.
Доказательство:
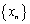 - б.м.п =>
- б.м.п => 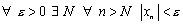 .
.
Возьмем любое  и положим
и положим  .
.
Тогда 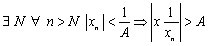
отсюда следует, что 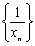 есть б.б.п.
есть б.б.п.
5. Пусть 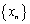 - б.б..п, тогда
- б.б..п, тогда 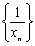 есть б.м.п.
есть б.м.п.
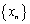 - б.б.п =>
- б.б.п => 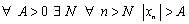 .
.
Возьмем любое 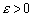 и положим
и положим 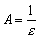
Тогда 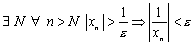 отсюда следует, что
отсюда следует, что 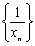 есть б.м.п.
есть б.м.п.
25. Вычисление предела:
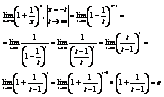
Понятие функции.
Пусть на некотором числовом множестве m определено правило, по которому каждому числу из множества m ставится в соответствии некоторое вещественное число. Тогда говорят, что на множество M задана функция. Множество M – называется областью определения этой функции. Обычно предполагают, что множество M представляет некоторый интервал, открытый или замкнутый ограниченный или ¥. Множество точек X принадлежащих множеству M будет образовывать на числовой оси некоторое множество. Это множество будет называться открытым, если вместе с любой точкой X из этого множества этому множеству M принадлежит некоторое ε окрестность X. Точка X Î M называется граничной точкой, если в любой e окрестности точки X можно указать точки, не принадлежащие множеству M. Множество М называется замкнутым, если дополнительное к нему множества является открытым R^\ M. Объединение любого числа отрытых множеств является открытым множеством, пересечение конечного числа множеств является открытым множеством. Следует, что пересечение любого числа замкнутых множеств являются замкнутым, объединение конечного числа замкнутых множеств являются замкнутыми. Пусть на множестве M определена функция. Это будем обозначать следующим образом: y = f(x), x Î M; x Î M  . Величина x будет называться независимой переменной или аргументом y значение, которой зависит от x - называется зависимой переменной или функцией. Рассмотрим на координатной плоскости множество точек G = {(x; f(x)), x Î M}. Множество G – называется графиком функции. Пусть на множестве M определены две функции y = f(x); y = g(x), тогда функция h(x) значение, которой вычисляется по правилу h(x) = f(x) + g(x) – является суммой. Функция h(x) = f(x)g(x) называется произведением. Функция может быть задана различными способами: 1) Графический способ 2) Словесный или сательный 3) Аналитический. Пусть на множестве x определена функция y = f(x) со значениями во множестве Y предположим, что на множестве Y определена функция со значениями множествам X x = g(y). Пусть при этом выполнены условия x = g(f(x)), y = f(g(y)). Тогда функция x =g(y) – называется обратной функциейпо отношению к функции y = f(x). Из определения следует, что функция y =f(x) так же является обратной функцией по отношению к функции x =g(y) по этому эти функции называются взаимно обратными. Примеры: 1)
. Величина x будет называться независимой переменной или аргументом y значение, которой зависит от x - называется зависимой переменной или функцией. Рассмотрим на координатной плоскости множество точек G = {(x; f(x)), x Î M}. Множество G – называется графиком функции. Пусть на множестве M определены две функции y = f(x); y = g(x), тогда функция h(x) значение, которой вычисляется по правилу h(x) = f(x) + g(x) – является суммой. Функция h(x) = f(x)g(x) называется произведением. Функция может быть задана различными способами: 1) Графический способ 2) Словесный или сательный 3) Аналитический. Пусть на множестве x определена функция y = f(x) со значениями во множестве Y предположим, что на множестве Y определена функция со значениями множествам X x = g(y). Пусть при этом выполнены условия x = g(f(x)), y = f(g(y)). Тогда функция x =g(y) – называется обратной функциейпо отношению к функции y = f(x). Из определения следует, что функция y =f(x) так же является обратной функцией по отношению к функции x =g(y) по этому эти функции называются взаимно обратными. Примеры: 1) 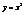 xÎ[0;¥] yÎ[0;¥]
xÎ[0;¥] yÎ[0;¥]  g(f(x)) =g
g(f(x)) =g  f(g(y))=
f(g(y))=  . 2)Пусть дана функция
. 2)Пусть дана функция 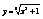 ;
; 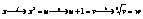 ; y = h(v) = h(g(u))®h(g(f(x))); y = f(x), x = g(y), y = f(g(y)), x = g(f(x)); g = lnx ,
; y = h(v) = h(g(u))®h(g(f(x))); y = f(x), x = g(y), y = f(g(y)), x = g(f(x)); g = lnx ,  , f(x) = lnx,
, f(x) = lnx, 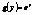 ,
, 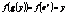 ,
,  3)
3) 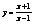 ,
, 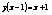 ,
, 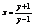 ;
; 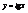 ,x = arctgy, tg(arctgy) = y, yÎ(-¥;¥), arctg (tgx) = x,
,x = arctgy, tg(arctgy) = y, yÎ(-¥;¥), arctg (tgx) = x,  .
.  график функции y = f (x),
график функции y = f (x), 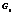 график функции x = g(y), тогда
график функции x = g(y), тогда  . Таким образом графики двух взаимно обратных функций совпадают, т. к. обычно через x обозначают независимую переменную, а через y зависимую переменную, то удобнее обратную функцию x = g(y) записывать в виде y = g(x) это приведет к тому, что график функции y = g(x) будет симметричен графику функции x =g(y), относительно биссектрисы одного координатного угла.
. Таким образом графики двух взаимно обратных функций совпадают, т. к. обычно через x обозначают независимую переменную, а через y зависимую переменную, то удобнее обратную функцию x = g(y) записывать в виде y = g(x) это приведет к тому, что график функции y = g(x) будет симметричен графику функции x =g(y), относительно биссектрисы одного координатного угла.
27. Предел функции в точке.
x = f(x), Xo ÎD(f) Xo – называется точкой сгущения, если в любой ее окрестности всегда можно указать точки из области определения функции y = f(x). Дальше всегда будем считать, что Xo точка сгущения. Число A называется пределом функции y =f(x), при  , если для любой числовой последовательности Xn сходящейся к Xo,
, если для любой числовой последовательности Xn сходящейся к Xo,  . Это определение эквивалентно следующему: A называется пределом функции f(x) при X ® Xo, если для любого числа e можно указать такое положительное число Δ, то из неравенства
. Это определение эквивалентно следующему: A называется пределом функции f(x) при X ® Xo, если для любого числа e можно указать такое положительное число Δ, то из неравенства 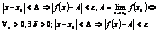 . Из свойств пределов следует: 1)
. Из свойств пределов следует: 1) 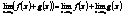 2)
2) 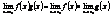 3)
3)  4)
4) 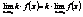 .
.
|
|
|
|
|
|
|
|
|
Дата добавления: 2018-05-02; просмотров: 244; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
