Полиномиальное интерполирование
Пусть функция задана множеством своих значений для дискретного набора точек
| 
|
| 
|
| 
|
| 
|
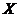
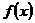
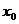
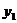
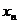
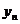
– табличные аргументы, 
– табличные значения функции (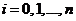 
).
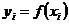(2.19.1)
Для восполнения исходных табличных функций искомыми функциями, как правило, используются алгебраические многочлены. Задача полиномиального интерполирования всегда имеет решение. Для оценки погрешности найдем остаточный член 
.
Если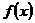 
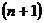раз дифференцируема на 
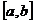и содержит узлы интерполирования 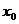, , …, , 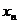то 
существует такая 
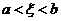, что выполняется
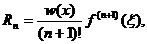
где 
.
Оценка интерполяции:
, (2.19.2)
где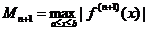 
.
Интерполяционный многочлен Лагранжа
Пусть исходная сеточная функция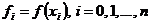 
задана в 
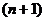узлах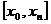 
в общем случае не равностоящих. Тогда многочлен Лагранжа имеет вид:
.
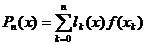Найдем коэффициенты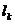 
.
,
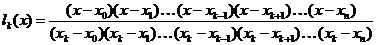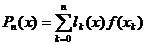. (2.19.3)
Пример 2.2.19.1.Заданы значения функции таблично, построить полином Лагранжа и найти значения функции в точке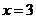 
, 
|
|
| 
| 
| |
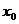
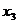
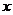
| 1 | 4 | 5 | 10 |
| 10 | 6 | 0 | 1 |
Решение.
Полином Лагранжа: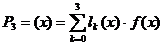 
, найдем коэффициенты
.
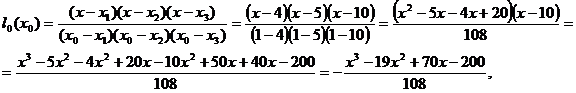
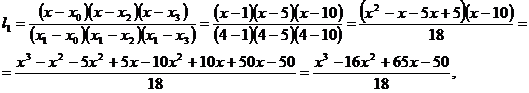
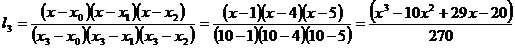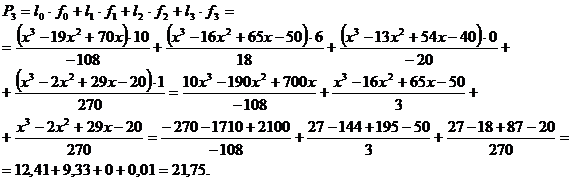
Интерполяционный многочлен Ньютона на неравномерной сетке
Известны значения функции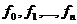 
для неравноотстоящих значений аргументов 
, тогда для построения полинома Ньютона применяются разделенные разности.
Разделенные разности первого порядка:
|
|
|
, 
.
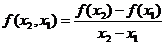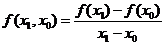По разделенным разностям первого порядка определяются разделенные разности второго порядка:
, 
.
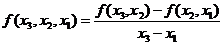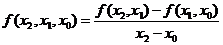В общем случае разделенные разности порядка n выражаются через функцию:
.
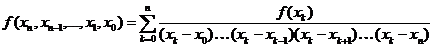Разделенные разности являются симметрической функцией своих аргументов.
Пусть исходная сеточная функция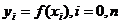 
задана на неравномерной сетке 
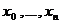c шагом 
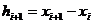. Тогда для функциональной интерполяции может быть использован многочлен Ньютона, основанный на разделенных разностях:
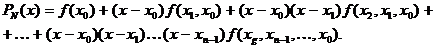
Пример 2.2.19.2.Заданы значения функции таблично, построить полином Лагранжа и найти значения функции в точке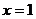 
, 
|
|
|
|
| |
|
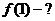
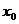
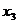
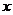
| –2 | –1 | 0 | 2 |
|
| –1 | 0 | 1 | 8 |
Решение.
Полином Ньютона:
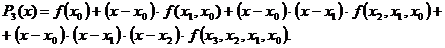
Найдем разделенные разности:
,
,
,
,
,
,
.
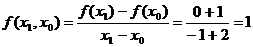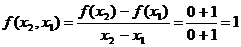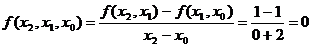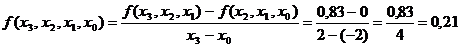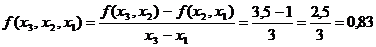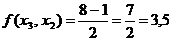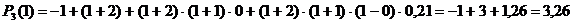Метод наименьших квадратов
Задана таблица значений аргументов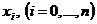 
и соответствующих значений функции 
.
На практике удобно представить искомую зависимость в виде многочлена, линейной комбинации некоторых базисных функций:
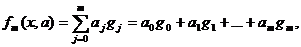(2.20.1)
где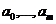 
– неизвестные коэффициенты, 
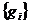– заданная система базисных функций. В качестве базисных функций могут выбираться, например, степенные функции, полиномы Чебышева, тригонометрические функции 
.
|
|
|
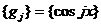Условия согласования метода сглаживания – метод наименьших квадратов:
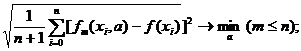. (2.20.2)
Отметим отличительные особенности решения задачи сглаживания методом наименьших квадратов:
1. Метод наименьших квадратов требует выполнения условия соответствия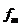 
и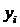 
в среднем.
2. Количество точек 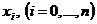, в которых задана исходная функция, значительно больше, чем степень многочлена.
Дата добавления: 2018-04-15; просмотров: 282; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!