Тема 1.4 Повторение испытаний
Независимые испытания
Формула Бернулли. Теорема Муавра-Лапласа. Интегральная теорема Лапласа. Формула Пуассона. Условия их применения
Литература: [2]; [4]; [5]; [6]; [7]; [8]; [9]; [12]; [13]; [14]
Вопросы для самоконтроля
1 Независимые испытания относительно события А. Формула Бернулли
2 Формула Пуассона, условия ее применения
3 Теорема Муавра-Лапласа, условия ее применения
4 Интегральная теорема Лапласа, условия ее применения
Методические рекомендации
Испытания называют независимыми относительно события А, если вероятность появления события А в каждом из проводимых испытаний не зависит от результатов предыдущих испытаний. Пусть вероятность появления события А в каждом единичном испытании равна р, а вероятность того, что это событие не произойдет, равна 1 – р = q. Тогда вероятность появления события А ровно m раз при проведении n испытаний определяется по формуле Бернулли:
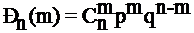 ,
, 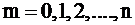 (20)
(20)
Если число испытаний n достаточно велико, а вероятность р достаточно мала (р < 0,1; npq < 10), то вероятность появления события А при многократном повторении испытаний можно приближенно вычислить по формуле Пуассона:
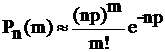 (21)
(21)
Теорема Муавра-Лапласа. Если число испытаний n достаточно велико, а вероятности p и q не очень близки к нулю (n > 100, npq > 20), то вероятность 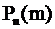 можно приближенно найти по локальной формуле Муавра-Лапласа:
можно приближенно найти по локальной формуле Муавра-Лапласа:
|
|
|
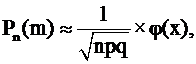 (22)
(22)
где 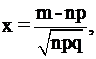
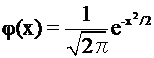 – функция Гаусса.
– функция Гаусса.
Таблица значений функции Гаусса приводится в приложениях.
Интегральная теорема Лапласа. В условиях локальной формулы Муавра-Лапласа вероятность 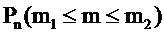 того, что число успехов m заключено между
того, что число успехов m заключено между 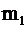 и
и 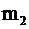 , можно приближенно найти по интегральной формуле Лапласа:
, можно приближенно найти по интегральной формуле Лапласа:
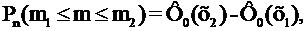 (23)
(23)
где 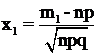 ,
, 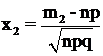 ,
,  – функция Лапласа.
– функция Лапласа.
Таблица значений функции Лапласа приводится в приложениях.
Раздел 2 Случайные величины
Тема 2.1 Дискретные случайные величины
Случайные величины, их виды. Закон распределения вероятностей дискретной случайной величины (ДСВ). Функция распределения случайной величины и ее свойства. Функция распределения ДСВ. Числовые характеристики ДСВ: математическое ожидание, дисперсия, среднее квадратическое отклонение. Свойства числовых характеристик дискретных случайных величин
Литература: [2]; [3]; [4]; [5]; [6]; [7]; [8]; [9]; [10]; [11]; [12]; [13]; [14]; [15]
Вопросы для самоконтроля
1 Случайная величина и закон ее распределения
2 Функция распределения случайной величины и ее свойства
3 Дискретная случайная величина
4 Математическое ожидание, дисперсия и среднее квадратическое отклонение дискретной случайной величины, их свойства
|
|
|
Методические рекомендации
Случайной величиной называют величину, которая в результате
испытания может принимать с определенной вероятностью разные значения.
Законом распределения случайной величины называется любое соответствие между значениями случайной величины  и их вероятностями
и их вероятностями 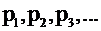 .
.
Пусть Х – некоторая случайная величина. Тогда функцию, ставящую в соответствие любому значению  вероятность того, что значение случайной величины Х меньше x:
вероятность того, что значение случайной величины Х меньше x:
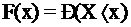 (24)
(24)
называют функцией распределения случайной величины Х. Функция распределения обладает следующими свойствами:
1) 0 ≤ F(x) ≤ 1 для всех 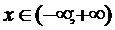 ;
;
2) F(х) – неубывающая функция;
3) 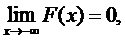

4) 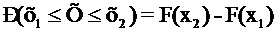 .
.
Случайную величину называют дискретной, если множество ее значений конечное либо счетное. Закон распределения дискретной случайной величины может быть задан таблицей, называемой рядом распределения:
| Х | 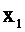
| 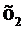
| … | 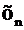
|
| Р | 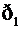
| 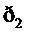
| … | 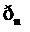
|
Важнейшими характеристиками случайной величины являются ее математическое ожидание М(Х), дисперсия D(X) и среднее квадратическое отклонение 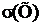 . Для дискретной случайной величины ее числовые характеристики вычисляются по следующим формулам:
. Для дискретной случайной величины ее числовые характеристики вычисляются по следующим формулам:
|
|
|
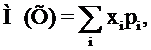 (25)
(25)
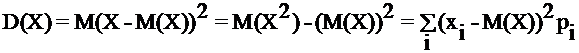 , (26)
, (26)
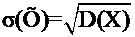 (27)
(27)
Дата добавления: 2018-05-02; просмотров: 227; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
