Расчетная формула метода Ньютона для нелинейного уравнения.
Пусть на отрезке 
имеется только один корень нелинейного уравнения 
. Расчетная формула метода Ньютона имеет вид:
, 
,
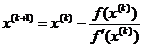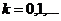где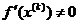 
, 
− заданное начальное приближение.
Идея метода Эйлера построения приближенного решения задачи Коши для обыкновенного диф. уравнения.
Рассматривается дифференциальное уравнение вида 
с начальным условием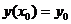 
. Требуется найти решение на отрезке , где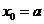 
. На отрезке вводится разностная сетка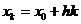 
, 
. Точки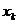 
называются узлами разностной сетки, а функции, заданные лишь в узлах сетки – сеточными. Приближённое решение задачи Коши будем искать численно в виде сеточной функции 
.
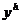Интегральная кривая согласно условию должна проходить через точку 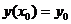и иметь в этой точке касательную. Тангенс угла наклона касательной к оси 
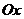равен значению производной от решения в точке 
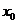и равен значению правой части дифференциального уравнения в точке 
: 
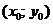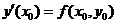. В случае небольшого шага h разностной сетки графики интегральной кривой и касательной не успевают сильно разойтись друг от друга, и можно в качестве значения решения в узле 
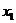принять значение касательной 
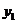вместо значения точного неизвестного решения. Считая теперь точку 
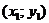начальной, повторяем предыдущие действия. Формула метода Эйлера имеет вид:
.
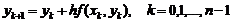Идея метода сеток.
Рассмотрим идею метода сеток для конкретного дифференциального уравнения в частных производных, а именно, уравнения Лапласа: 
. Ясно, что этому уравнению удовлетворяют многие функции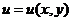 
. Конкретный вид функции 
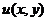зависит от граничных условий, т.е. от значений функции на границах области изменения переменных 
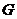, которые задаются пользователем. Идея состоит в том, что вместо отыскания аналитической формулы 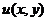во всей области 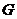, определить приближенные значения функции в некоторых точках внутри области 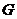, как правило, образующих сетку. В двумерных областях проще использовать прямоугольную сетку, разбивая область 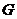вдоль осе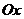й и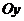 
на части с одинаковым шагом 
. Приближенные значения производных в каждом узле выбранной сетки записывают, используя информацию о значениях искомой функции 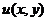в соседних узлах. Для частных производных разностные формулы принимают вид 
, 
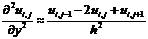, подстановка которых в уравнение Лапласа дает уравнение
|
|
|
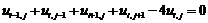. (14.1)
Рассмотрим конкретный пример сетки, эскиз которой приведен на рисунке. Здесь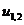 
, 
, 
, 
, 
, 
, 
, 
, 
, 
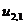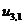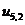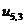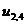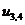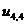− заданные граничные условия, 
, 
, 
, 
, 
, 
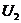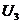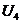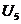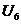− значения функции в узлах сетки, подлежащие определению. Применяя формулу (14.1) для каждой внутренней точки области, получаем СЛАУ из 6 уравнений относительно 6 неизвестных 
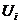, которую можно решить любым известным методом (прямым или итерационным).
|
|
|
Если пользователю необходима непрерывная функция, то ее можно получить, например, используя двумерную сплайн-интерполяцию на основе найденных дискретных значений .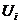 
Дата добавления: 2018-04-15; просмотров: 250; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!