Идея приближенного вычисления определенного интеграла методами трапеций и прямоугольников.
Пусть непрерывная функция 
задана на отрезке 
. Требуется вычислить интеграл 
. Пользуясь геометрическим смыслом определённого интеграла, можно заменить задачу отыскания первообразной на подсчёт площади под кривой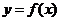 
. Для этого следует разбить промежуток на n одинаковых отрезков длиной h: 
; затем подсчитать приближённо площадь под кривой на каждом частичном отрезке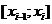 
тем или иным способом, а окончательный результат получить суммированием площадей.
Формула трапеций: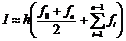 
, где 
.
Формула центральных прямоугольников: 
, где 
.
Формула левых прямоугольников: 
, где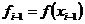 
.
Формула правых прямоугольников: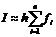 
, где 
.
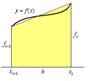
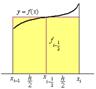
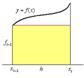
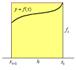
Формулы левых и правых прямоугольников имеют первый порядок точности по 
, а формулы трапеций и центральных прямоугольников – второй. Ниже на рисунках представлена графическая иллюстрация формул.
Определение нормы матрицы.
Нормой матрицыA (обозначается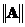 
) с вещественными элементами называется неотрицательное число, вычисляемое с помощью элементов матрицы и обладающее следующими свойствами:
1) 
, 
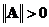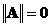тогда и только тогда, когда A - нулевая матрица;
2) 
;
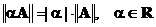3) 
;
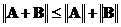4) 
.
9. Определение 1-, 2- и ∞-норм векторов и 1-, евклидовой (Фробениуса) и ∞-норм матриц.
Пусть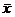 
− вектор в пространстве 
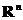, тогда
1-норма вектора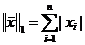 
,
2-норма вектора 
,
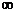-норма вектора 
.
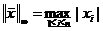Пусть 
− вещественная матрица порядков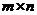 
, тогда
1-норма матрицы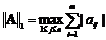 
,
наибольшее значение среди сумм абсолютных значений элементов в каждом столбце;
|
|
|
евклидова норма (Фробениуса) матрицы 
,
все элементы матрицы возводим в квадрат, суммируем и извлекаем корень;
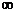-норма матрицы 
,
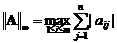наибольшее значение среди сумм абсолютных значений элементов в каждой строке.
Определение числа обусловленности матрицы.
Пусть − квадратная вещественная матрица, тогда число обусловленности матрицы:
.
Матрица плохо обусловлена, если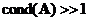 
.Для вырожденной матрицы полагают 
.
Расчетная формула для итерационного процесса и условие сходимости.
Метод простых итераций применяется для решения систем линейных алгебраических уравнений (СЛАУ) из n уравнений c n неизвестными, если основная матрица системы не вырождена, т.е.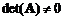 
:
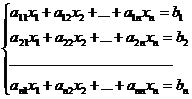. (11.1)
СЛАУ в матричной форме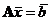 
необходимо преобразовать к виду 
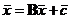. (11.2)
Один из способов преобразования (метод Якоби) состоит в том, что из первого уравнения системы (11.1) выражаем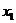 
, из второго 
и т.д. Далее выбираем начальное приближение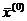 
и подставляем его в правую часть уравнения (11.2) , тем самым находим первое приближение 
; подставляем первое приближение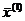 
в правую часть уравнения (11.2) и находим второе приближение 
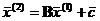и т.д.
|
|
|
Расчетная формула дляk-ой итерации имеет вид
.
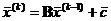Процесс можно прекратить, когда значения неизвестных в последней и предпоследней итерации совпадают до требуемой точности (например, до трёх знаков после запятой).
Достаточное условие сходимости: метод простых итераций сходится к единственному решению СЛАУ при любом начальном приближении 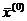, если какая-либо норма матрицы B системы (11.2) меньше единицы: 
.
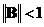Дата добавления: 2018-04-15; просмотров: 244; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!