Нові доведення основних теорем.
Покажемо тепер як Лема Бореля може бути використана для доведення основних теорем про неперервні функції.
І. Перша теорема Больцано-Коші. Нехай функція 
неперервна на відрізку 
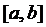і приймає на кінцях відрізка значення різних знаків. Тоді в інтервалі 
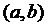найдеться точка, значення функції в якій рівне нулю, тобто 
.
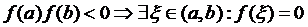Доведення
Цього разу доводити її будемо від супротивного. Припустимо, що – при дотримані припущення теореми – все ж в жодній точці функція не перетворюється в нуль. Тоді кожну точку 
проміжку 
можна обмежити таким околом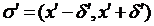 
, що в його межах зберігає певний знак.
Нескінченна система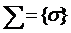 
цих околів покриває весь проміжок . Тоді, згідно леми Бореля, буде існувати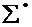 
околів, яка покриє даний відрізок ( 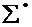– скінченна).
Лівий кінець a нашого проміжку належить одному із околів системи 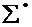, нехай околу 
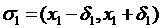. Його правий кінець 
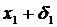, в свою чергу, належить околу 
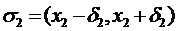із 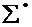, точка 
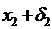міститься в околі (інтервалі) 
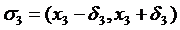із 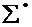, і т. д.
Після скінченного числа кроків, рухаючись вправо, ми дійдемо до околу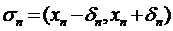 
із 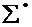, який містить в собі правий кінець b даного проміжку. Якби 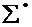містила ще якійсь інші проміжки, крім 
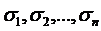, то їх, очевидно, можна було би просто не врахувати.
В околі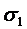 
функція зберігає певний знак, саме знак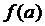 
. Проте і в 
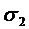функція має визначений знак, який повинен також співпадати із знаком 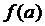, оскільки 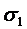і 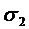взаємно налягають. Також переконуємося в тому, що цей знак функція зберігає і в наступному по порядку околі 
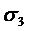, який налягає на 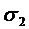, і т.д. В кінці-кінців, прийдемо до висновку, що і в останньому околі 
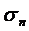функція має знак 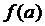, так що 
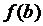співпадає по знаку із 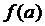. Отримали суперечність.
|
|
|
Теорема доведена.
Проміжне значення неперервної на відрізку функції. Метод дихотомії.
Припустимо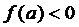 
, 
. Поділимо відрізок пополам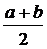 
. Можливі три випадки:
1. 
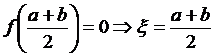, тобто теорема доведена.
2. 
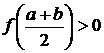. Покладемо 
, 
.
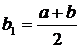3. 
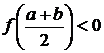. Покладемо 
, 
.
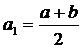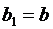Отримаємо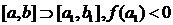 
, 
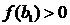. Знову поділимо отриманий відрізок точкою 
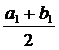. Знов-таки можливі три випадки:
1. 
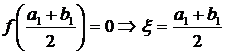, тобто теорема доведена.
2. 
. Покладемо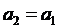 
, 
.
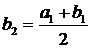3. 
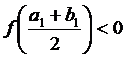. Покладемо 
, 
.
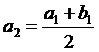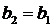Отримаємо: 
, 
.
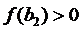Продовжимо процес побудови таких відрізків. На (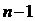 
)-му кроці маємо:
, 
.
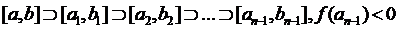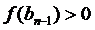Розділимо даний відрізок 
на 2 частини точкою 
. Знову маємо три випадки:
1. 
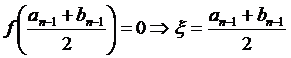, тобто теорема доведена.
2. 
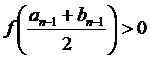. Покладемо 
, 
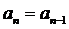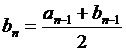
3. 
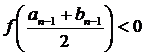. Покладемо 
, 
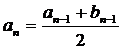, отримаємо
, 
.
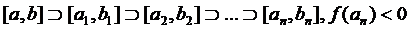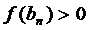Довжина n-го відрізка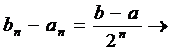 
0,
, 
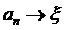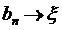при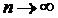 
(згідно з лемою про вкладені відрізки). 
, 
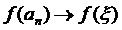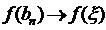, через неперервність функції.
Одночасно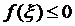 
(так як 
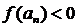) і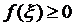 
(так як 
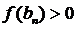), тобто 
.
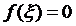Теорема доведена.
Геометричний зміст теореми Больцано-Коші полягає в тому, що неперервна функція перетинає вісь Ox хоча б один раз.
ІІ.Перша теорема Вейєрштрасса. Якщо функція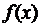 
неперервна на сегменті , то вона обмежена на цьому сегменті, тобто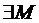 
, 
.
|
|
|
Доведення.
В силу неперервності функції 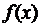, яку би точку x 
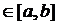ми не взяли, знайдеться таке число 
, що можна виділити як завгодно малий окол цієї точки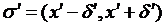 
, так щоб для всіх його значень x виконувалися б нерівності:
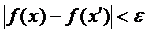, або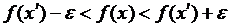 
.
Таким чином, в межах кожного такого околу функція 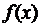наперед обмежена: знизу – числом 
, а зверху – числом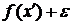 
.
Зрозуміло, що тут до нескінченної системи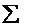 
околів, які володіють вказаною властивістю потрібно застосувати лему Бореля. З неї випливає, що знайдеться в 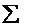скінченне число околів 
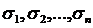, які в сукупності покриють весь відрізок 
. Якщо:
Поклавши 
і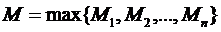 
. Очевидно будемо мати 
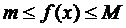на всьому проміжку .
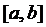Теорема доведена.
ІІІ. Теорема Кантора. Якщо функція 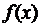неперервна на сегменті , то вона рівномірно неперервна на цьому сегменті.
Доведення.
Задамося довільним числом 
. На цей раз кожну точку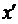 
проміжку обмежимо таким околом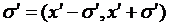 
, щоб в його межах виконувалася нерівність: 
.
Якщо x0 також точка цього околу, то одночасно і 
. Таким чином, для будь-яких точок x та x0 із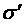 
будемо мати: 
.
|
|
|
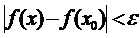Стягнемо кожен окіл 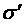вдвічі, зберігаючи його центр, тобто замість 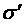розглянемо окіл: 
.
Із цих околів відповідно складеться система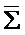 
, яка покриває відрізок , і саме до неї ми застосуємо лему Бореля. Проміжок покриється скінченним числом відрізків із :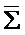
.
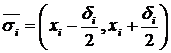
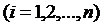Нехай тепер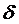 
буде найменшим із цих всіх чисел 
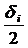, і x0, x – будь-які дві точки нашого проміжку, що задовольняють умову:
. (*)
Точка x0 повинна належати одному із виділених околів, наприклад, околу:
, так що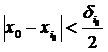 
.
Оскільки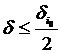 
, то , згідно (*), 
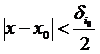, звідки 
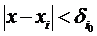, тобто точка x (тим більше точка x0) належить тому початковому взятому околу: 
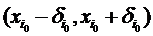, стисненням якого отримаємо окіл 
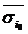. В цьому випадку, в силу властивостей раніше взятих околів, отримаємо: 
.
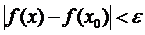Оскільки 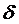було вибране незалежно від положення точки x0, рівномірна неперервність функції 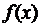доведена.
Теорема доведена.
Як видно з приведених міркувань, лема Бореля з успіхом застосовується в тих випадках, коли «локальна» властивість, зв’язана з околом окремої точки, підлягає розповсюдженню на весь розглядуваний проміжок.
Контрольні запитання.
1. Сформулювати і довести лему Гейне-Бореля.
2. Дати означення копактності множини через покриття.
|
|
|
3. Довести першу теорему Больцано-Коші про існування кореня рівнянь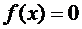 
за допомогою леми Гейне-Бореля.
4. Сформулювати лему Гейне-Бореля в довільному абстрактному просторі.
5. Довести за допомогою леми Гейне-Бореля, теорему Кантора про рівномірну неперервність числової функції 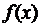, яка неперервна на сегменті .
Вправи.
1. Довести за допомогою леми Гейне-Бореля, першу теорему Вейєрштрасса про обмеженість числової функції, яка неперервна на сегменті .
Розв’язання.
1. Оскільки функція 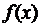неперервна, то яку б точку 
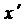відрізка ми не взяли, задавши число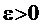 
, ми можемо взяти досить малий окіл 
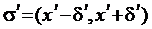такий, щоб для всіх точок x околу виконувались нерівності 
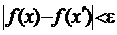або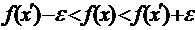 
. Множина цих околів утворює нескінченне покриття сегменту . В межах кожного такого околу функція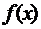 
є наперед обмеженою: знизу – числом 
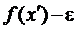, а зверху – числом 
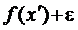. За лемою Гейне-Бореля, з даного нескінченого покриття можна виділити скінченне під покриття. Якщо
то взявши в якості m найменше з чисел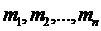 
, а в якості M – найбільше з чисел M1,M2,...,Mn, очевидно, будемо мати
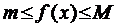
на всьому сегменті , що і потрібно було довести.
Дата добавления: 2018-04-15; просмотров: 685; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!