Оценки погрешности метода простой итерации

Теорема 3.2 [3]. Пусть 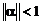, тогда выполняется

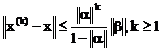,                                         (3.12)

где х^(k) – к-ое приближение, х – точное решение.

Доказательство.

Пусть х^(о)=(0, 0,…, 0), тогда из (3.11) имеем

х^(k)=(Е+a+a²+…+a^k-1)b.

Точное решение

х=(Е+a+a²+…+a^k-1)b+(a^k+a^k+1+…)b.

Тогда, вычитая из первого равенства второе и оценивая нормы, получим

 ,

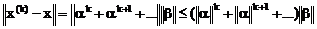где 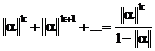. Тогда имеем

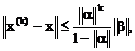 что и требовалось доказать.

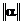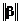Оценка (3.12) называется априорной оценкой погрешности и позволяет оценить погрешность к-го приближения, не проведя вычислений, используя, нормы  и . Также при заданной точности вычисления e можно определить необходимое число итераций из формулы .

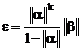Теорема 3.3 [3]. Пусть 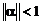, тогда имеет место неравенство

.

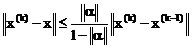Доказательство.

Пусть имеем приведенную систему линейных уравнений

х=b+aх.                                                                    (3.13)

Тогда для к-го приближения имеем

х^(к)=b+aх^(к-1).                                                            (3.14)

Из (3.13) и (3.14) получим

х^(к)-х=a(х^(к-1)-х).                                                       (3.15)

Прибавим к левой и правой части этого равенства х^(к-1) и тогда имеем

х^(к-1)-х= х^(к-1)-х^(к)+a(х^(к-1)-х). Откуда

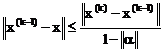.                                         (3.16)

Из (3.15) получим

,                                           (3.17)

тогда из (3.16) и (3.17) имеем

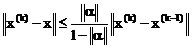,                                  (3.18)

что и требовалось доказать.

Оценка (3.18) называется апостериорной оценкой погрешности, так как её получают по известной 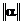 и вычисленным приближениям х^(к-1) и х^(к).

 

Метод Зейделя

Метод Зейделя [3,4,9,11]представляет собой некоторую модификацию метода простой итерации. Основная идея метода заключается в том, что при вычислении (к+1)-го приближения неизвестной x_i  учитываются уже вычисленные ранее (к+1)-ые приближения неизвестных x_1, x₂, …, x_n.

Пусть имеется приведенная линейная система

x_i=b_i+ 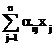, (i=1, 2, …, n).

Выберем произвольно начальные приближения

.

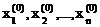Далее, предполагая, что к-ые приближения неизвестных 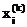 вычислены, построим формулы для (к+1)-го приближения:

,

,

………………………………….

,

………………………………….

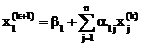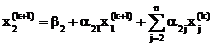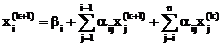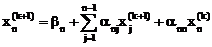, (k=0, 1, 2,…).

Таким образом, алгоритм метода Зейделя для решения СЛАУ будет следующим

,

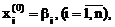
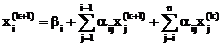a_ii=0, k=0, 1, 2, …

Итерация заканчивается по выполнению условия

для всех ;

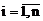где 0<e<1.

Отметим, что теорема 3.1 и следствия 3.1 и 3.2 верны и для метода Зейделя.

Формулы для оценки погрешности метода Зейделя следующие [3]:

а) по m – норме

где

,

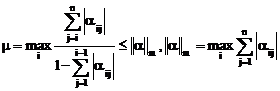б) по l – норме

,

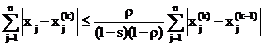где

.

 

Метод релаксации

Имеем систему уравнений

                                (3.19)

Для описания метода релаксации [2, 3, 9, 11] преобразуем систему (3.19) следующим образом. Перенесем свободные члены налево и разделим первое уравнение на -а₁₁, второе на -а₂₂ и т.д. Тогда получим

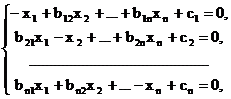                       (3.20)

где b_ij=-a_ij/a_ii , (i¹j), c_i=b_i/a_ii , (i,j=1, 2,…, n).

Пусть х⁽⁰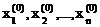⁾=( ) – начальное приближение, тогда подставляя его в (3.20) получим невязки

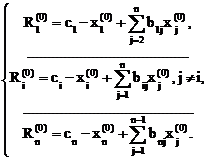                                   (3.21) 

Еслив (3.21) одной из неизвестных 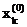 дать приращение d 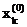, то соответствующая невязка  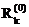уменьшится на d  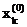, а остальные невязки  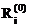  (i¹к) увеличатся на величину b_ikd 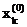, (i=1, 2,…, n; i¹k; k=1, 2,…,n ).

Следовательно, чтобы обратить невязку 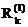 в нуль, достаточно величине  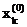дать приращение

 d = ,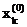

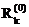тогда будем иметь следующую систему уравнений на первой итерации

= ,

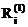далее, чтобы на m – ой итерации обратить в нуль невязку 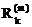 дадим переменной  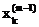приращение

d = .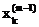

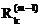Тогда получим систему уравнений

= .

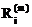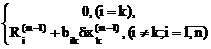Процесс итерации заканчивается, когда все невязки последней преобразованной системы будут равны нулю с требуемой точностью.

В методе рекомендуется на каждой итерации обращать в нуль максимальную по модулю невязку путем изменения значения, соответствующей компоненты приближения.

Алгоритм метода релаксации будет таким.

Задается начальное приближение

х⁽⁰⁾=( ).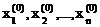

Вычисляются невязки начального приближения

.

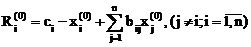Находим величину а_к= 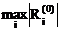, которой соответствует невязка  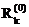и приращение

d = .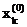

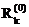Дальше вычисляются невязки первого приближения

=  

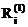и т.д.

Затем находим величину а_к= 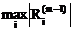, которой соответствует невязка  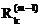и приращение

d 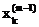= 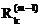, что позволяет вычислить невязку m-го приближения

=

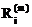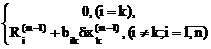
и т.д. m=m+1, m+2,…, M. M®¥.

Итерация заканчивается при выполнении условия

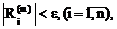где 0<e<1.

Неизвестные вычисляются по формуле

x_i=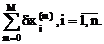

 

Замечание. Описанный здесь метод называется полной релаксацией. Если в процессе полной релаксации для системы уравнений (3.19) с положительно-определенной матрицей выполнено условие: Последовательность индексов i компонент x_i (i=1, 2,…, n) имеет интервал повторяемости L , т.е. на каждом отрезке длины L индекс i принимаетхотя быпо одному разу все числа 1, 2,…, n , то процесс сходится к решению системы (3.19), где L – любое натуральное число.

---

Дата добавления: 2018-04-15; просмотров: 1173; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!