Тема 2. Системы координат. Действия над векторами
В координатной форме
10. Декартова система координат
Введение базиса в пространстве позволяет перейти от геометрических соотношений между векторами к соотношениям между их координатами. Однако базисов бесконечно много. Кроме этого, бесконечно много точек, в которых мы можем совместить начала векторов. Поэтому вводят понятие системы координат.
Определение. Система координат – совокупность фиксированной точки, называемой началом координат, и фиксированного базиса.
Чаще всего на практике используют прямоугольную декартову систему координат (ПДСК). Тогда в качестве базисных векторов фиксируют единичные векторы, которые попарно перпендикулярны. На плоскости приходим к системе координат 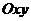 .
.
Рассмотрим декартову систему координат в пространстве. В качестве базисных векторов выбираем векторы 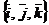 , считая
, считая 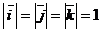 ,
, 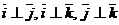 . Такой базис называют ортонормированным, а векторы
. Такой базис называют ортонормированным, а векторы  – ортами координатных осей.
– ортами координатных осей.
Всюду далее будем рассматривать правую тройку базисных векторов 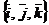 , т.е. с конца вектора
, т.е. с конца вектора  поворот
поворот 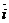 до положительного направления
до положительного направления 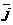 «видим» как движение против часовой стрелки (в случае левой тройки это движение «видим» по часовой стрелке).
«видим» как движение против часовой стрелки (в случае левой тройки это движение «видим» по часовой стрелке).
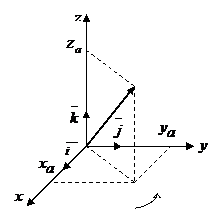
|
|
|
|
В пространстве ПДСК имеет три плоскости: 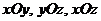 . Эти плоскости делят трехмерное пространство на 8 частей – октантов. I-й октант тот, где направления
. Эти плоскости делят трехмерное пространство на 8 частей – октантов. I-й октант тот, где направления  положительны.
положительны.
20. Переход к координатным соотношениям между векторами
Рассмотрим прямоугольную декартову систему координат в пространстве с базисом 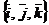 . Используя понятие разложения вектора по базисным векторам и понятие координат в базисе, получаем
. Используя понятие разложения вектора по базисным векторам и понятие координат в базисе, получаем
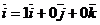 , т.е.
, т.е. 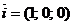 .
.
Аналогично:
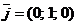 ;
;  .
.
Вектор, начало которого совпадает с началом системы координат называется радиус-вектором.
Согласно общей теории всякий вектор 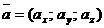 можно однозначно разложить по базисным векторам (по базису)
можно однозначно разложить по базисным векторам (по базису)
 .
.
30. Действия над векторами в координатной форме
Рассмотрим векторы 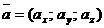 ,
, 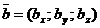 .
.
Геометрически вектор  является диагональю прямоугольного параллелепипеда, который имеет измерения
является диагональю прямоугольного параллелепипеда, который имеет измерения 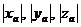 . Согласно теореме из стереометрии для длины диагонали выполняется
. Согласно теореме из стереометрии для длины диагонали выполняется
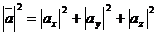 ,
,
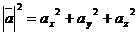 ,
,
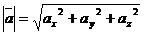 . (1)
. (1)
Поскольку координаты вектора в ПДСК – проекции на соответствующие оси, то согласно свойствам линейности проекции:
 ;
;
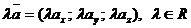 .
.
Рассмотрим задание вектора 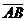 координатами начала и конца
координатами начала и конца 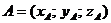 ,
, 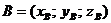 .
.
|
|
|
|

Формула (2) – формула вычисления координат вектора по координатам его начала и конца.
Допустим, что некоторый отрезок  делится точкой
делится точкой  в отношении
в отношении 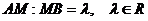 , т.е.
, т.е. 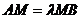 . Произведя соответствующие построения в ПДКС можно доказать следующие формулы для нахождения координат точки
. Произведя соответствующие построения в ПДКС можно доказать следующие формулы для нахождения координат точки  :
:
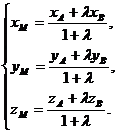
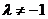 (3)
(3)
При 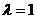 точка
точка  будет серединой отрезка.
будет серединой отрезка.
Определение. Направляющими косинусами вектора  называются косинусы углов
называются косинусы углов 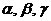 , которые образует этот вектор с координатными осями
, которые образует этот вектор с координатными осями 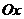 ,
, 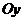 ,
,  соответственно.
соответственно.
Используя формулу для проекции вектора на ось имеем:
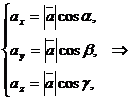 (4)
(4)
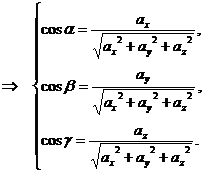 (5)
(5)
Из формул (5) можно найти углы, которые образует вектор  с координатными осями.
с координатными осями.
Если равенство (5) возвести в квадрат и сложить, получим
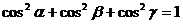 .
.
Рассмотрим единичный вектор  . Тогда из (4)
. Тогда из (4)

Последнее означает, что координаты всякого единичного вектора равны направляющим косинусам.
|
|
|
Если 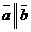 , то существует число
, то существует число 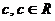 такое, что
такое, что  . Тогда
. Тогда
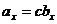 ,
, 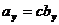 ,
, 
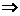
 ,
, 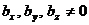 .
.
Координаты коллинеарных векторов пропорциональны.
Дата добавления: 2018-04-15; просмотров: 530; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 ось абсцисс;
ось абсцисс;
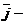 ось ординат;
ось ординат;
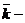 ось аппликат.
ось аппликат.
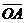 и
и 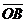 :
:
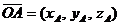 ;
; 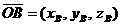 .
Согласно правилу вычитания векторов:
.
Согласно правилу вычитания векторов:
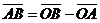
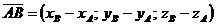 (2)
(2)