Угол между прямой и плоскостью
Угол α между нормальным вектором плоскости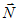 
и направляющим вектором прямой 
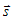вычисляется по формуле:
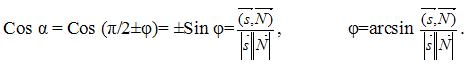
Пучок плоскостей
Совокупность всех плоскостей, проходящих через заданную прямую L, называется пучком плоскостей, а прямая L - осью пучка. Пусть ось пучка задана уравнениями
Почленно умножим второе уравнение системы на постоянную и сложим с первым уравнением:
A1x+B1y+C1z+D1+ λ(A2x+B2y+C2z+D2)=0.
Это уравнение имеет первую степень относительно х, у, z и, следовательно, при любом численном значении λопределяет плоскость. Так как данное уравнение есть следствие двух уравнений, то координаты точки, удовлетворяющие этим уравнениям будут удовлетворять и данному уравнению. Следовательно, при любом численном значении λданное уравнение есть уравнение плоскости, проходящей через заданную прямую. Полученное уравнение есть уравнение пучка плоскостей.
ПримерНаписать уравнение плоскости, проходящей через точку M1(2, -3, 4) параллельно прямым
Решение.Запишем уравнение связки плоскостей, проходящих через данную точку M1:
А (х - 2) + В (у + 3) + C(z - 4) = 0.
Так как искомая плоскость должна быть параллельна данным прямым, то ее нормальный вектор должен быть перпендикулярен направляющим векторам 
этих прямых. Поэтому в качестве вектора N можно взять векторное произведение векторов 
:
Следовательно, А = 4, В = 30, С = - 8. Подставляя найденные значения А, В, С в уравнение связки плоскостей, получим
|
|
|
4(x-2)+30(y + 3) -8(z-4) =0 или 2x + 15у - 4z + 57 = 0.
ПримерНайти точку пересечения прямой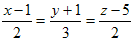 
и плоскости 2х + 3y-2z + 2 = 0.
Решение. Запишем уравнения данной прямой в параметрическом виде:
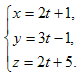
Подставим эти выражения для х, у, z в уравнение плоскости:
2(2t+1)+3(3t-1)-2(2t+5)+2=0 Þ t=1.
Подставим t = 1 в параметрические уравнения прямой. Получим
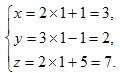
Итак, прямая и плоскость пересекаются в точке М(3, 2, 7).
ПримерНайти угол φ между прямой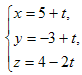 
и плоскостью 4x-2y-2z+7=0.
Решение. Применяем формулу (3.20). Так как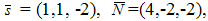 
то
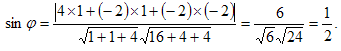
Следовательно,φ = 30°.
ПРЯМАЯ В ПРОСТРАНСТВЕ
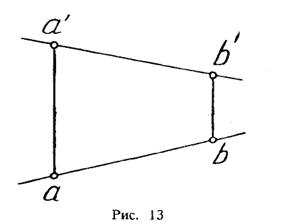
Прямая линия в пространстве бесконечна, поэтому задавать ее удобнее отрезком. Из школьного курса Евклидовой геометрии известна аксиома, «через две точки в пространстве можно провести прямую и, притом, только одну». Следовательно, на эпюре прямая может быть задана двумя фронтальными и двумя горизонтальными проекциями точек. Но так как прямая — это прямая (а не кривая), то с полным основанием мы можем соединить эти точки отрезком прямой и получить фронтальную и горизонтальную проекции прямой (рис.13).
Доказательство от обратного: в плоскостях проекций V и Н заданы две проекции а' b' и ab (рис.14). Проведем через них плоскости, перпендикулярные к плоскостям проекций V и Н (рис.14), линией пересечения плоскостей будет прямая АВ.
|
|
|
Дата добавления: 2018-04-15; просмотров: 324; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!