Ротор векторного поля. Формула Стокса
Потенциальное поле.
Потенциальное (или безвихревое) векторное поле в математике — векторное поле, которое можно представить как градиент некоторой скалярной функции координат (потенциала). Необходимым условием потенциальности векторного поля в трёхмерном пространстве является равенство нулю ротора поля. Однако это условие не является достаточным (например, вмногосвязной области у безвихревого поля может не существовать скалярный потенциал).
Пусть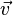 
— потенциальное векторное поле; оно выражается через потенциал 
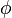как
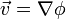(или в другой записи 
).
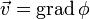Для поля сил и потенциала сил эта же формула записывается как
,
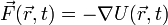то есть для сил потенциалом 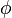является 
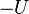. Когда U не зависит от времени, оно является потенциальной энергией, и тогда знак «-» возникает просто по определению. В противном случае знак сохраняется ради единообразия.
Для поля 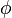выполняется свойство независимости интеграла от пути 
:
,
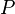Это равносильно
.
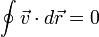Интеграл по замкнутому контуру обращается в 0, поскольку начальная и конечная точка совпадают. И наоборот, предыдущую формулу можно вывести из этой, если разбить замкнутый контур на два незамкнутых.
Необходимое условие записывается как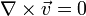 
(или в другой записи 
).
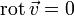Комплексные числа. Основные понятия.
Ко́мпле́ксные чи́сла (устар. мнимые числа) — числа вида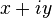 
, где 
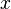и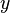 
— вещественные числа, 
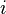— мнимая единица; то есть 
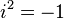. Множество всех комплексных чисел обычно обозначается 
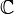от лат. complex — тесно связанный.
Первоначально идея о необходимости расширения понятия действительного числа возникла в результате формального решения квадратных и кубических уравнений, в которых в формулах для корней уравнения под знаком корня стояло отрицательное число. В дальнейшем возникшая теория функций комплексного переменного нашла применение для решения многих задач во всех областях математики и физики.
Стандартная модель:
Комплексное число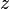 
можно определить как упорядоченную пару вещественных чисел 
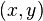; запись 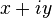следует понимать как удобный способ записи пары .
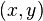Введём операции сложения и умножения таких пар следующим образом:
· 
· 
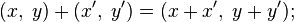
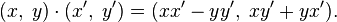
Вещественные числа являются в этой модели подмножеством множества комплексных чисел и представлены парами вида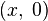 
, причём операции с такими парами согласованы с обычными сложением и умножением вещественных чисел. Ноль представляется парой 
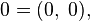единица — 
а мнимая единица — 
. На множестве комплексных чисел ноль и единица обладают теми же свойствами, что и на множестве вещественных, а квадрат мнимой единицы, как легко проверить, равен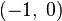 
, то есть 
.
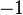Несложно показать, что определённые выше операции имеют те же свойства, что и аналогичные операции с вещественными числами. Исключением являются только свойства, связанные сотношением порядка (больше-меньше), потому что невозможно расширить порядок одиночных чисел, включив в него такие упорядоченные пары чисел, чтобы операции отношения порядка по-прежнему были согласованы.
Матричная модель:
Комплексные числа можно также определить как семейство вещественных матриц вида
с обычным матричным сложением и умножением. Действительной единице будет соответствовать
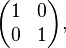
мнимой единице —
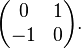
Дата добавления: 2018-04-04; просмотров: 589; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!