Численное дифференцирование функции
П.4 Тригонометрическая интерполяция.
1.В тригонометрической интерполяции в отличие от других видов интерполяции, интерполяция происходи не по  , а по
, а по  точкам, т.к. интерполирование происходит периодически и
точкам, т.к. интерполирование происходит периодически и  , т.е. период
, т.е. период 
2.  ,
,  - равноотстоящие узлы интерполяции.
- равноотстоящие узлы интерполяции.
4.1.Формулы Т.И.:

(4.18а)
где 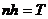 , (4.18б)
, (4.18б)
Замечание:
в этих формулах i– мнимая единица и для работы по (4.18а) , (4.18б) нужна формула Эйлера: 
При Т.И. интерполирующая функция y(x):
1) периодична с периодом 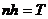 .
.
2) в узлах интерполяции  , т.е. если
, т.е. если  -вещественное, то в узлах мнимая часть y – нулевая.
-вещественное, то в узлах мнимая часть y – нулевая.
3) в промежуточных точках у может принимать комплексные значения, но Im y – будет не велика и её можно отбросить.
4) если число узлов интерполяции нечётное, т.е. n=2n+1, и все  - вещественные, то функция у полученная по (4.18а) , (4.18б) сама по себе будет вещественна.
- вещественные, то функция у полученная по (4.18а) , (4.18б) сама по себе будет вещественна.
Коэффициенты  - комплексные, а
- комплексные, а  - вещественные функции и в этом случае вычисления можно осуществлять не с комплексными, а с вещественными числами по формуле (4.19).
- вещественные функции и в этом случае вычисления можно осуществлять не с комплексными, а с вещественными числами по формуле (4.19).
(4.19а) 
(4.19б) 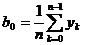 ;
; 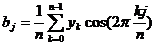 ;
; 

Быстрое преобразование Фурье.
Определение: преобразование набора значений функции (y0…yn-1) в набор коэффициентов (A0…An-1) (используя (4.18б)), участвующих в разложении Фурье, называется прямым преобразованием Фурье (ППФ), а обратным преобразованием Фурье (ОПФ) – преобразование массива Aj в yk (по (4.18б)).
Если осуществлять эти вычисления непосредственно по (4.18а, б), то трудоёмкость -  (т.к. имеем n коэффициентов, в каждом из которых n слагаемых).
(т.к. имеем n коэффициентов, в каждом из которых n слагаемых).
Эти же вычисления можно делать по более быстрым формулам – быстрое преобразование Фурье. Трудоёмкость по этим формулам существенно меньше: не 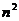 , а
, а  .
.
Многомерная интерполяция.
Пусть мы имеем функцию нескольких переменных, значения которой нам известны в некоторых точках (при задаче интерполирования нам надо знать значение функции f в наперед заданной точке).
Решим простой вариант двумерной интерполяции f(x,y):
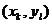 - узлы образующие прямоугольную сетку.
- узлы образующие прямоугольную сетку.
 1)Интерполируем функцию по х (при фиксированном у) и получим значение функции в точке х.
1)Интерполируем функцию по х (при фиксированном у) и получим значение функции в точке х.
При фиксированном х, 1 раз интерполируем по у (по
3-м  ) и получим значение в точке
) и получим значение в точке  .
.
2)х и у можно поменять местами и сделать интерполяцию по у и 1 раз по х.
Значения полученные этими способами весьма близки к точным значениям функции, близки друг к другу, но могут и различаться.
П.5. Применение интерполяции.
Обратная интерполяция.
С помощью обратной интерполяции можно решать нелинейные уравнения.
Решим f(x)=a:
Идея обратной интерполяции: пусть f в близи корня уравнения f(x)=a – монотонно возрастает или убывает, тогда у неё существует обратная функция.
g(x) – обратная функция, значение которой в точке а нас не интересует.
f(x)=a ; 
и будет искомым корнем уравнения f(x)=a, 
Возьмём интервал  , на котором f – монотонна и имеет обратную функцию, следовательно, мы знаем
, на котором f – монотонна и имеет обратную функцию, следовательно, мы знаем 
Применим интерполяцию для вычисления значений обратной функции g и найдем значение интерполирующей функции в точке а. Это и будет, приблизительно, искомый корень.
x=g(a)
При этом при интерполяции х и у меняются местами, так как мы интерполируем не f а g.
Пример:
| х | 10 | 15 | 17 | 20 |
| у | 3 | 7 | 11 | 17 |
f(x)=10
Решение находим интерполируя обратную функцию по 4-м точкам (например, по формуле Лагранжа).

Численное дифференцирование функции.
Дата добавления: 2018-04-05; просмотров: 314; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
