Дробный факторный эксперимент

⇐ ПредыдущаяСтр 3 из 18Следующая ⇒

С увеличением количества факторов, согласно методу полного факторного эксперимента, резко возрастает общее число опытов. Однако для нахождения коэффициентов регрессии не всегда требуется полное число опытов, определяемое полным факторным экспериментом. Если воспользоваться методом дробного факторного эксперимента, то можно уменьшить общее число опытов. Этот метод заключается в том, что для нахождения уравнения коэффициентов регрессии используется некоторая часть полного факторного эксперимента: 1/2, 1/4, 1/8 и т. д. Такие части полного факторного эксперимента называются дробными репликами.

Эксперимент, реализующий часть (дробную реплику) полного факторного эксперимента, называется дробным факторным экспериментом (ДФЭ). ДФЭ позволяет получить приближение искомой функциональной зависимости Y=f(X₁, …, X_n) в некоторой небольшой окрестности точки базового режима при минимуме опытов.

Применение ДФЭ всегда связано со смешиванием, т.е. совместной оценкой нескольких коэффициентов уравнения связи. Коэффициенты не могут быть найдены раздельно, поскольку столбцы матрицы для линейных членов и парных произведений совпадают (полностью скоррелированы). При большом числе переменных можно построить дробные реплики высокой степени дробности (1/4, 1/8, 1/16 и т.д.). Дробная реплика обозначается через 2^n—p, если p переменных приравнены к соответствующим произведениям переменных.

Экзаменационный билет

Что называют задачами оптимизации? Приведите примеры задач оптимизации. Что такое экстремальный эксперимент?

Под оптимизациейпонимают процесс выбора наилучшего варианта из всех возможных. С точки зрения инженерных расчетов методы оптимизации позволяют выбрать наилучший вариант конструкции, наилучшее распределение ресурсов и т. п.

В процессе решения задачи оптимизации обычно необходимо найти оптимальные значения некоторых параметров, определяющих данную задачу.В качестве проектных параметров могут быть, в частности, значения линейных размеров объекта, массы, температуры и т. п. Число п проектных параметров x₁,x₂,…,x_п характеризует размерность (и степень сложности) задачи оптимизации.

Выбор оптимального решения или сравнение двух альтернативных решений проводится с помощью некоторой зависимой величины (функции), определяемой проектными параметрами. Эта величина называется целевой функцией(или критерием качества). В процессе решения задачи оптимизации должны быть найдены такие значения проектных параметров, при которых целевая функция имеет минимум (или максимум). Таким образом, целевая функция — это глобальный критерий оптимальности в математических моделях, с помощью которых описываются инженерные или экономические задачи.

Задачи оптимизации.

Можно выделить два типа задач оптимизации — безусловные и условные. Безусловная задача оптимизации состоит в отыскании максимума или минимума действительной функции от действительных переменных и определении соответствующих значений аргументов на некотором множестве а n-мерного пространства.

Условные задачи оптимизации, или задачи с ограничениями, — это такие, при формулировке которых задаются некоторые условия (ограничения) на множестве а. Эти ограничения задаются совокупностью некоторых функций, удовлетворяющих уравнениям или неравенствам.

Ограничения равенствавыражают зависимость между проектными параметрами, которая должна учитываться при нахождении решения. Эти ограничения отражают законы природы, наличие ресурсов, финансовые требования и т. п.

Следует отметить особенность в отыскании решения при наличии ограничений. Оптимальное решение здесь может соответствовать либо локальному экстремуму (максимуму или минимуму) внутри области проектирования, либо значению целевой функции на границе области. Если же ограничения отсутствуют, то ищется оптимальное решение на всей области проектирования, т. е. глобальный экстремум.

Задачи на экстремум.

Одномерная задача оптимизациив общем случае формулируется следующим образом. Найти наименьшее (или наибольшее) значение целевой функции у = f(x), заданной на множестве cr, и определить значение проектного параметра х е а, при котором целевая функция принимает экстремальное значение. Существование решения поставленной задачи вытекает из следующей теоремы.

Теорема Вейерштрасса. Всякая функция f(x), непрерывная на отрезке [а, b], принимает на этом отрезке наименьшее и наибольшее значения, т. е. на отрезке [а, b] существуют такие точки х₁ и x₂, что для любого х £ [а,b] имеют место неравенства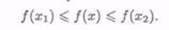

Пример. Найти наименьшее и наибольшее значения функции f ’ (x) = x³/3 - х² на отрезке [1,3].

Решение. Вычислим производную этой функции:

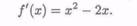
Приравнивая ее нулю, найдем критические точки:

Точка х = 0 лежит вне рассматриваемого отрезка, поэтому для анализа оставляем три точки: а = 1, x-i — 2, b = 3. Вычисляем значения функции в этих точках:

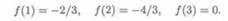
Сравнивая полученные величины, находим, что наименьшего значения функция f(x) достигает в точке х = 2, наибольшего — в точке х = 3, т. е.

Дата добавления: 2018-04-04; просмотров: 627; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!