БИНС с одним уравнением Пуассона
Рассмотрим другой способ определения параметров ориентации. Обратимся к дифференциальному уравнению
.
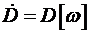Подставляя
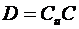
получим
откуда
.
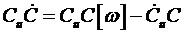Используя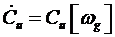 
, получим
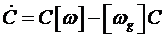
Таким образом, для получения матрицы ориентации достаточно решить это одно дифференциальное уравнение, получившее название обобщенного уравнения Пуассона.
Блок –схема алгоритма БИНС для этого случая показана на рисунке
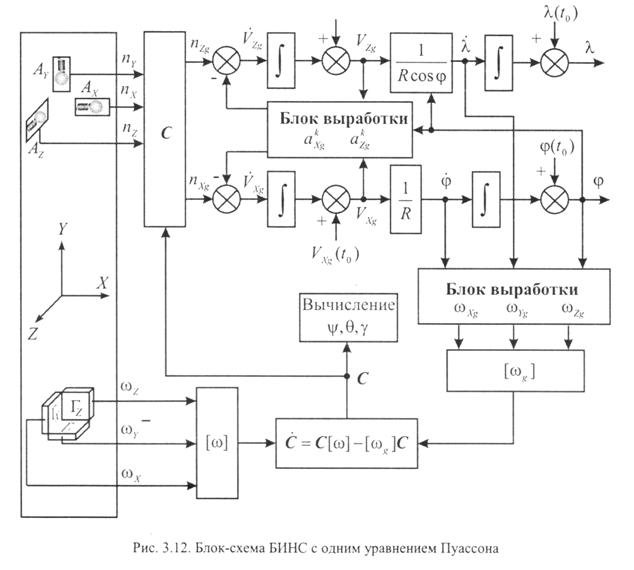
БИНС с параметрами Родрига-Гамильтона
Эффективным средством повышения точности и экономичности является использование параметров Родрига-Гамильтона. При одинаковой точности использование этих параметров дает экономию в объеме вычислений в среднем на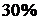 
.
Ось конечного поворота.
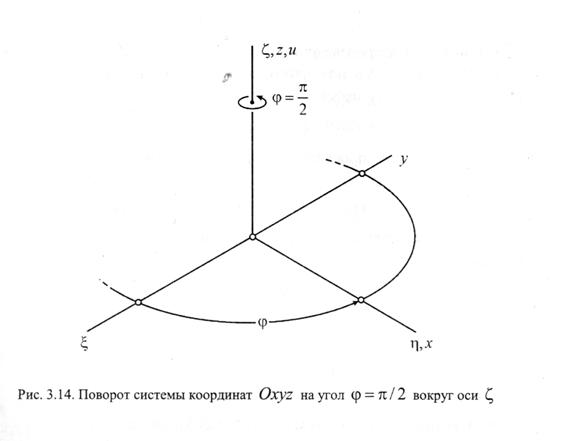
Рассмотрим понятие оси конечного поворота.
Пусть система координат 
поворачивается относительно неподвижной системы координат 
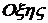на произвольный угол 
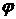вокруг некоторой оси 
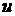, называемой осью конечного поворота.
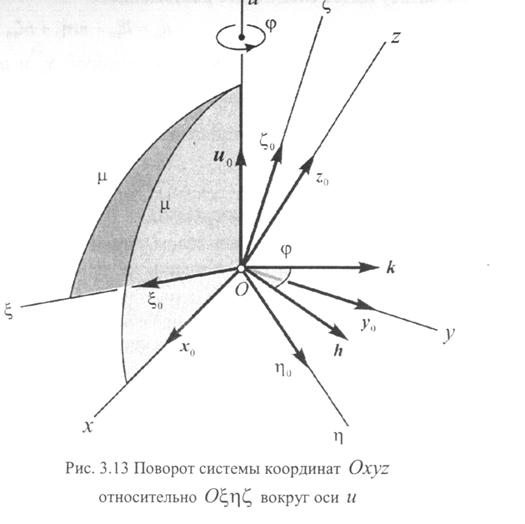
Обозначим через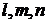 
косинусы углов, которые образует ось 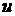с осями системы координат 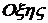. Очевидно, что эти величины являются косинусами углов и с осями системы координат ( см. Рисунок)
,
,
.
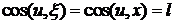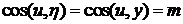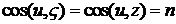В частности имеем
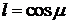
где 
-угол, который образует ось вращения 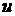и с осью 
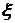и с осью 
системы координат 
.
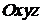Обозначим направляющие косинусы оси относительно системы координат 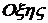соответственно через 
.
, 
, 
.
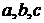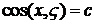Направляющие косинусы удовлетворяют уравнению
|
|
|
.
Выразим направляющие косинусы оси через направляющие косинусы 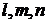оси конечного поворота 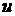и угол поворота .
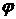Очевидно, что проекция единичного вектора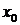 
оси на оси системы координат 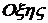равны 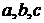. Тогда разложение этого вектора по базису 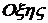имеет вид
.
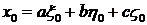В свою очередь, разложение вектора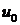 
по этому базису имеет вид
.
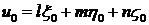Найдем скалярное произведение векторов 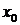и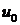
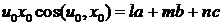
или с учетом того, что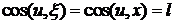
.
Для определения трех искомых величин 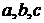кроме этого уравнения и уравнения
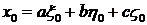
требуется еще одно уравнение. Для вывода этого уравнения воспользуемся тем обстоятельством, что плоскость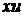 
повернута относительно плоскости 
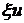на угол 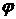. Так как двугранный угол измеряется углом между перпендикулярами к образующим его плоскостям то введем два вектора 
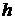и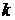 
первый из которых перпендикулярен плоскости 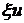, а второй плоскости 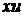. (См. Рисунок)
Согласно свойству скалярного произведения двух векторов имеем
,
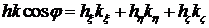где 
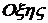-проекции на оси вектора , 
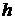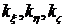-проекции на те же оси вектора .
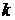В качестве вектора 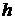возьмем векторное произведение единичных векторов 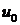и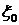 
.
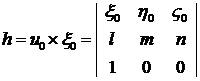Как следствие,
, 
, 
.
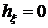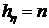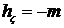В качестве вектора 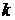возьмем векторное произведение 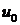и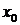
Раскрывая определитель, получим
, 
, 
.
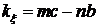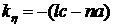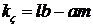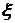Модули векторных произведений (*) и (**) одинаковы и равны синусу угла между осями и 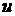или , что то же самое, между осями и 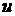( см. Рисунок). Таким образом, будем иметь
|
|
|
.
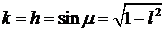С учетом найденных проекций уравнение
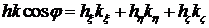
примет вид
(***)
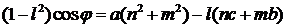которое и является третьим уравнением для определения .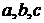
Так как
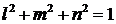
то
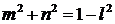и из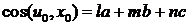 
вытекает равенство
.
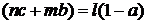Тогда уравнение (***) примет вид
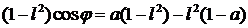
и после несложных преобразований получаем
.
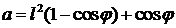Для определения величины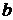 
используем уравнение
из которого исключаем найденное значение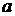 
и значение 
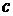с учетом уравнения
. (*)
Получим квадратное уравнение
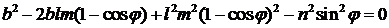
Из двух корней этого уравнения
, 
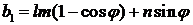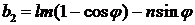
используется первое
Используя полученные значения 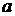и 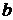из (*) можно найти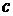
.
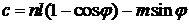Аналогично определяются косинусы углов между осью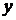 
и осями 
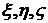и далее между осью 
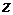и осями 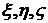. В итоге таблица косинусов между осями примет вид
В этой таблице величины 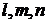-косинусы углов, которая образует ось поворота 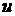с осями 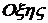, а также с осями .
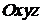Параметры Родрига-Гамильтона
Каждому повороту тела на угол 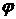вокруг оси 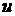с направляющими косинусами 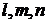заданными относительно исходной системы координат 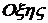ставятся в соответствие четыре числа, называемые параметрами Родрига –Гамильтона:
|
|
|
, 
, 
, 
.
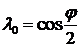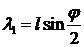Параметры Родрига –Гамильтона связаны между собой очевидным соотношением
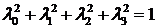
Учитывая, что
, 
,
элемент (1,1) таблицы может быть представлен в виде
.
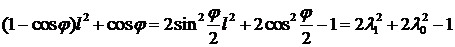Учитывая, что
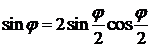
элемент (1,2) таблицы будет равен
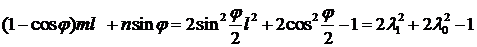
Рассчитывая элементы таблицы аналогичным образом можно получить таблицу
Если, например вместо осей 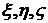использовать оси географической системы координат 
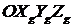, а вместо 
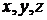-оси связанной системы координат , то полученная матрица будет аналогом матрицы направляющих косинусов
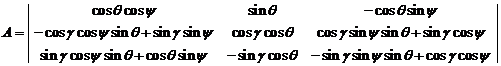
Таким образом, взаимное положение двух систем координат помимо трех углов Эйлера-Крылова, девяти направляющих косинусов, можно определить с помощью четырех параметров Родрига- Гамильтона.
Кватернионы
Определенные удобства в вычислении параметров Родрига- Гамильтона дают кватернионы-гиперкомплексные числа вида
с одной действительной и тремя мнимыми единицами.
Величины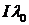 
и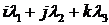 
называют соответственно скалярной и векторными составляющими кватернионов и обозначаются
,
.
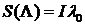Следовательно кватернион можно представить в виде
.
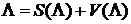Кватернион сопряженный данному кватерниону определяется выражением
|
|
|
.
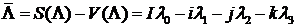Кватернион можно рассматривать как вектор в четырехмерном пространстве длина которого называется тензором или модулем кватерниона
.
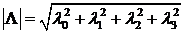Дата добавления: 2018-04-05; просмотров: 1345; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!