Метод покоординатного спуску. Алгоритм розрахунку
Введение
Рассмотрим задачу поиска минимума функции 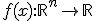 , записываемую в виде:
, записываемую в виде:
(1)
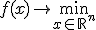
В этой статье описан метод покоординатного спуска, решающий поставленную задачу. Также приведена теорема сходимости метода покоординатного спуска.
Метод покоординатного спуска
Алгоритм
Вход: функция 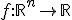
Выход: найденная точка оптимума 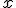
1. Инициализация некоторым значением 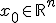
2. повторять:
§ для 
1. фиксируем значения всех переменных кроме 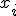 , получая одномерную функцию
, получая одномерную функцию 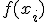
2. проводим одномерную оптимизацию по переменной 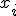 , любым методом одномерной оптимизации
, любым методом одномерной оптимизации
3. если выполен критерий останова (варианты описаны ниже), то возвращаем текущее значение 
Критерий останова
Критерии остановки процесса приближенного нахождения минимума могут быть основаны на различных соображениях. Некоторые из них:
1. 
2. 
Здесь  - значение, полученное после
- значение, полученное после 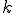 -го шага оптимизации.
-го шага оптимизации.  - наперед заданное положительное число.
- наперед заданное положительное число.
Сходимость метода
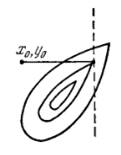
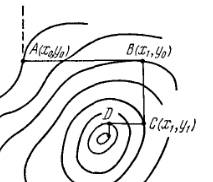
Легко убедится, что существуют функции, когда метод координатного спуска не приводит даже в локальный оптимум.
Пусть линии уровня образуют истинный овраг (рис.2), когда спуск по любой координате приводит на <<дно>> оврага, а любое движение по следующей координате (пунктирная линия) ведет на подъем. Никакой дальнейший спуск по координатам в данном случае невозможен, хотя минимум еще не достигнут.
Теорема о сходимости метода покоординатного спуска.
|
|
|
Для простоты рассмотрим функцию двух переменных 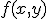 . Выберем некоторое начальное приближение
. Выберем некоторое начальное приближение  и проведем линию уровня через эту точку. Пусть в области
и проведем линию уровня через эту точку. Пусть в области 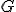 , ограниченной этой линией уровня, выполняются неравенства, означающий положительную определенность квадратичной формы:
, ограниченной этой линией уровня, выполняются неравенства, означающий положительную определенность квадратичной формы:
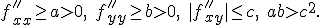
Тогда спуск по координатам сходится к минимуму из данного начального приближения, причем линейно.
Приклад побудови канонічної форми задачі ЛП
Загальна лінійна економіко-математична модель економічних процесів та явищ – так звана загальна задача лінійного програмування подається у вигляді:
 (3.1)
(3.1)
за умов:
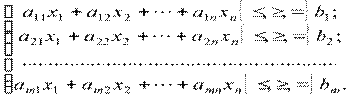 (3.2)
(3.2)
 (3.3)
(3.3)
Отже, потрібно знайти значення змінних x1, x2, …, xn, які задовольняють умови (3.2) і (3.3), і цільова функція (3.1) набуває екстремального (максимального чи мінімального) значення.
Для довільної задачі математичного програмування у п.2.1 були введені поняття допустимого та оптимального планів.
Умовний та безумовний екстремуми функції
У теорії дослідження функцій задача на відшукання екстремальних значень не містить ніяких додаткових умов щодо змінних і такі задачі належать до задач відшукання безумовного екстремуму функції. Локальний та глобальний екстремуми тоді визначаються з необхідних та достатніх умов існування екстремуму функції.
|
|
|
Нагадаємо, що необхідна умова існування локального екстремуму функції двох змінних формулюється так: для того, щоб точка 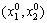 була точкою локального екстремуму, необхідно, щоб функція
була точкою локального екстремуму, необхідно, щоб функція  була неперервною і диференційовною в околі цієї точки і перші частинні похідні за змінними
була неперервною і диференційовною в околі цієї точки і перші частинні похідні за змінними 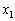 та
та 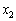 у цій точці дорівнювали нулю:
у цій точці дорівнювали нулю:
 .
.
Точка 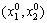 називається критичною.
називається критичною.
Достатня умова існування локального екстремуму функції двох змінних формулюється так: для того, щоб критична точка 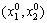 була точкою локального екстремуму, достатньо, щоб функція
була точкою локального екстремуму, достатньо, щоб функція  була визначена в околі критичної точки
була визначена в околі критичної точки 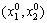 та мала в цій точці неперервні частинні похідні другого порядку.
та мала в цій точці неперервні частинні похідні другого порядку.
Тоді, якщо
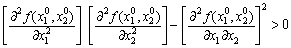 ,
,
то в точці 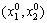 функція
функція  має екстремум, причому, якщо
має екстремум, причому, якщо
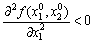 ,
,
тоді 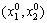 — точка локального максимуму функції
— точка локального максимуму функції  , а якщо
, а якщо
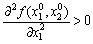 ,
,
тоді 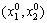 — точка локального мінімуму функції
— точка локального мінімуму функції  .
.
У разі, якщо
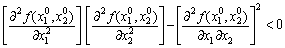 ,
,
то в точці 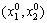 функція
функція  екстремуму не має.
екстремуму не має.
Якщо
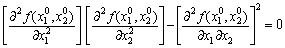 ,
,
то питання про існування екстремуму залишається відкритим.
Якщо задача полягає у відшуканні локального чи глобального екстремуму деякої функції за умови, що на змінні такої функції накладаються додаткові обмеження, то маємо задачу пошуку умовного екстремуму функції. Термін «умовний» означає, що змінні задачі мають задовольняти деякі умови.
|
|
|
Розглянемо таку задачу для випадку двох змінних:
знайти 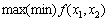 (8.4)
(8.4)
за умови, що 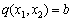 . (8.5)
. (8.5)
Найпростіший спосіб розв’язання задачі такого виду полягає в тому, що спочатку з обмеження (8.5) знаходять вираз однієї змінної через іншу. Приміром, визначають 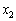 через
через 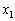 . Отриманий вираз виду
. Отриманий вираз виду  підставляють у функцію (8.4), що після цього стає функцією однієї змінної
підставляють у функцію (8.4), що після цього стає функцією однієї змінної 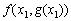 , і далі знаходять її безумовний екстремум.
, і далі знаходять її безумовний екстремум.
Якщо деяка точка  є точкою екстремуму функції
є точкою екстремуму функції 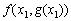 , то точка
, то точка  є точкою умовного екстремуму функції (8.4) за умови (8.5).
є точкою умовного екстремуму функції (8.4) за умови (8.5).
Однак не завжди вдається відшукати аналітичний вираз однієї змінної через іншу в умові (8.5). Часто це досить важко здійснити або неможливо. Також іноді складно узагальнити даний спосіб для функції n змінних, на які накладено m обмежень. Тому описана досить проста ідея зведення задачі відшукання умовного екстремуму функції кількох змінних до задачі на безумовний екстремум функції однієї змінної не може бути використана як основа універсального методу розв’язування задач на умовний екстремум. Цікавий метод розв’язування задач типу (8.4), (8.5) запропонував Лагранж.
|
|
|
Критерий оптимальности
КРИТЕРИЙ ОПТИМАЛЬНОСТИ [optimality criterion] — фундаментальное понятие современной экономики (которая переняла его из математического программирования и математической теории управления); применительно к той или иной экономической системе это один из возможных критериев (признаков) еекачества, а именно тот признак, по которому производится сравнение вариантов и один или несколько из них признаются наилучшими из возможных (в данных объективных условиях).
Применительно к конкретным экономическим решениям К. о. — показатель, выражающий предельную меру экономического эффекта от принимаемого решения для сравнительной оценки возможных решений (альтернатив) и выбора наилучшего из них. Это может быть максимум прибыли, минимум затрат, кратчайшее время достижения цели и т. д.
К. о. — важнейший компонент любой оптимальной экономико-математической модели. Чем больше (если нас интересует максимум) или чем меньше (если нужен минимум) показатель К. о., тем больше удовлетворяет нас решение задачи. Если решается задача составления хозяйственного плана, то это означает, что выбран наилучший, оптимальный план: все остальные варианты не могут дать столь же удовлетворительного результата. Если решается, напр., задача исследования операций по организации строительства завода, то это означает, что выбраны наилучшая очередность работ, наиболее рациональное распределение сил и ресурсов и т. д., а все другие варианты приведут к более поздним срокам пуска завода.
К. о. носит обычно количественный характер, т. е. он применяется для того, чтобы качественный признак плана, выражаемый соотношением “лучше—хуже”, переводить в количественно определенное “больше — меньше”. Но применяются и порядковые критерии. В последнем случае определяется лишь то, что один вариант лучше или хуже других, но не выясняется, насколько именно.
В экономико-математических задачах К. о. соответствует математическая форма — целевая функция, экстремальное значение которой (см. Экстремум) характеризует предельно достижимую эффективностьмоделируемого объекта (т. е. наилучшие в заданном отношении структуру, состояние, траекториюразвития). Другим возможным выражением К. о. является шкала (оценок полезности, ранжированияпредпочтений и т. д.).
В реальной практике планирования К. о. не может и не должен носить жесткого однозначного характера. Оперируя с ним, следует иметь в виду такие факторы, как вероятное изменение условий, возникновение новых возможностей реализации плана, а также новых задач. Приходится поэтому поступаться величиной критериального показателя ради гибкости плана и его надежности. Это достигается как формальными, так и неформальными методами.
На схеме к ст. “Экономическая система” (рис. Э. 2) стрелка W имеет направление, соответствующее движению в сторону лучшего качества результатов функционирования экономической системы, т. е. лучшего удовлетворения потребностей общества в материальных благах. Упорядоченность точек шкалыW (и соответственно шкал U1, ..., Un) принято формализовать с помощью целевой функции F(w), которая отождествляется с К. о.
Упорядочение точек шкалы W, как и точек шкал U, есть субъективный акт. Оно может строиться в зависимости от того, чту понимается под целью данной экономической системы, но с учетом ее реальных возможностей (объективная основа) и качества управления системой (субъективная основа). Способы упорядочения различны:
а) установление цели внешним по отношению к данной экономической системе или иным обладающим соответствующими правами субъектом управления;
б) согласование тем или иным способом шкал предпочтения самостоятельных субъектов управления (социальных групп, организаций и т. д.), принимающих решения исходя из своих интересов — компромисс, правило большинства и другие понятия группового (социального) выбора.
Возможна классификация К. о.:
а) по уровню общности — глобальный критерий оптимального развития в масштабе планеты, социально-экономический критерий, народнохозяйственный критерий, а также глобальныйилокальные критерииоптимальности в частных системах моделей;
б) по временному аспекту — статические и динамические (среди последних — оценивающие развитие от неоптимального к оптимальному состоянию и развитие как смену оптимальных состояний), текущие и финишные; критерии быстродействия (т. е. времени достижения цели);
в) по способам формирования критериев — нормативные, социолого-статистические, компромиссные, унитарные и т. д.;
г) по типу применяемых измерителей — полезностные, стоимостные, натуральные и др.;
д) по способам использования критериев — практические, теоретические, политико-пропагандистские;
е) по математической формализации — скалярные и векторные критерии, аддитивные и мультипликативные, интегральные критерии (во временном аспекте) и интегральные (в пространственном аспекте) и др. (см. скаляр, вектор, мультипликатор).
Таковы лишь наметки классификации К. о., однако предстоит еще немало сделать для ее отработки, унификации и стандартизации.
5. методи пошуку безумовного екстремуму однієї змінної.
Умовний та безумовний екстремуми функції
У теорії дослідження функцій задача на відшукання екстремальних значень не містить ніяких додаткових умов щодо змінних і такі задачі належать до задач відшукання безумовного екстремуму функції. Локальний та глобальний екстремуми тоді визначаються з необхідних та достатніх умов існування екстремуму функції.
Нагадаємо, що необхідна умова існування локального екстремуму функції двох змінних формулюється так: для того, щоб точка 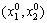 була точкою локального екстремуму, необхідно, щоб функція
була точкою локального екстремуму, необхідно, щоб функція  була неперервною і диференційовною в околі цієї точки і перші частинні похідні за змінними
була неперервною і диференційовною в околі цієї точки і перші частинні похідні за змінними 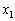 та
та 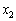 у цій точці дорівнювали нулю:
у цій точці дорівнювали нулю:
 .
.
Точка 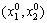 називається критичною.
називається критичною.
Достатня умова існування локального екстремуму функції двох змінних формулюється так: для того, щоб критична точка 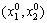 була точкою локального екстремуму, достатньо, щоб функція
була точкою локального екстремуму, достатньо, щоб функція  була визначена в околі критичної точки
була визначена в околі критичної точки 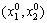 та мала в цій точці неперервні частинні похідні другого порядку.
та мала в цій точці неперервні частинні похідні другого порядку.
Тоді, якщо
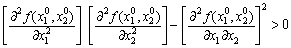 ,
,
то в точці 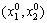 функція
функція  має екстремум, причому, якщо
має екстремум, причому, якщо
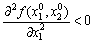 ,
,
тоді 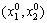 — точка локального максимуму функції
— точка локального максимуму функції  , а якщо
, а якщо
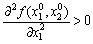 ,
,
тоді 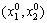 — точка локального мінімуму функції
— точка локального мінімуму функції  .
.
У разі, якщо
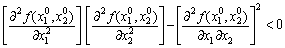 ,
,
то в точці 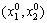 функція
функція  екстремуму не має.
екстремуму не має.
Якщо
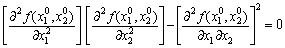 ,
,
то питання про існування екстремуму залишається відкритим.
Якщо задача полягає у відшуканні локального чи глобального екстремуму деякої функції за умови, що на змінні такої функції накладаються додаткові обмеження, то маємо задачу пошуку умовного екстремуму функції. Термін «умовний» означає, що змінні задачі мають задовольняти деякі умови.
Розглянемо таку задачу для випадку двох змінних:
знайти 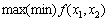 (8.4)
(8.4)
за умови, що 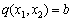 . (8.5)
. (8.5)
Найпростіший спосіб розв’язання задачі такого виду полягає в тому, що спочатку з обмеження (8.5) знаходять вираз однієї змінної через іншу. Приміром, визначають 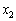 через
через 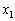 . Отриманий вираз виду
. Отриманий вираз виду  підставляють у функцію (8.4), що після цього стає функцією однієї змінної
підставляють у функцію (8.4), що після цього стає функцією однієї змінної 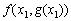 , і далі знаходять її безумовний екстремум.
, і далі знаходять її безумовний екстремум.
Якщо деяка точка  є точкою екстремуму функції
є точкою екстремуму функції 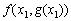 , то точка
, то точка  є точкою умовного екстремуму функції (8.4) за умови (8.5).
є точкою умовного екстремуму функції (8.4) за умови (8.5).
Однак не завжди вдається відшукати аналітичний вираз однієї змінної через іншу в умові (8.5). Часто це досить важко здійснити або неможливо. Також іноді складно узагальнити даний спосіб для функції n змінних, на які накладено m обмежень. Тому описана досить проста ідея зведення задачі відшукання умовного екстремуму функції кількох змінних до задачі на безумовний екстремум функції однієї змінної не може бути використана як основа універсального методу розв’язування задач на умовний екстремум. Цікавий метод розв’язування задач типу (8.4), (8.5) запропонував Лагранж.
21. До методів дискретної оптимізації і лінійного програмування часто доводиться звертатись при аналізі і виборі рішень в конфліктних ситуаціях, тобто при наявності сторін, що мають на меті відмінні (найчастіше – протилежні) цілі. Стратегією гравця називають сукупність правил, що визначають поведінку гравця від початку гри до її завершення. Задання стратегій 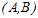 двох гравців в парній грі повністю визначає її наслідок, тобто виграш одного і програш другого. Гра називається скінченною, якщо в кожного гравця є лише скінченна кількість стратегій. Результати скінченної парної гри з нульовою сумою можна задавати матрицею, рядки і стовпці якої відповідають відмінним стратегіям, а її елементи - відповідні виграші однієї сторони (які дорівнюють програшам другої).
двох гравців в парній грі повністю визначає її наслідок, тобто виграш одного і програш другого. Гра називається скінченною, якщо в кожного гравця є лише скінченна кількість стратегій. Результати скінченної парної гри з нульовою сумою можна задавати матрицею, рядки і стовпці якої відповідають відмінним стратегіям, а її елементи - відповідні виграші однієї сторони (які дорівнюють програшам другої).
Розглянемо гру  з матрицею
з матрицею

Якщо перший гравець застосовує стратегію  , то другий буде прагнути до того, щоб вибором відповідної стратегії
, то другий буде прагнути до того, щоб вибором відповідної стратегії 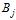 звести виграш першого гравця до мінімуму. Величина цього мінімуму, яку ми позначимо
звести виграш першого гравця до мінімуму. Величина цього мінімуму, яку ми позначимо 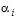 , дорівнює, очевидно,
, дорівнює, очевидно,  . З точки зору першого гравця (при будь-яких відповідях супротивника) доцільно прагнути знайти таку стратегію, при якій
. З точки зору першого гравця (при будь-яких відповідях супротивника) доцільно прагнути знайти таку стратегію, при якій 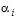 перетворюється в максимум. Цей максимум, який ми позначимо
перетворюється в максимум. Цей максимум, який ми позначимо 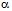 , називається нижньою ціною гри. Оскільки значення
, називається нижньою ціною гри. Оскільки значення 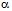 обчислюється за формулою
обчислюється за формулою 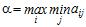 , то його називають також максиміном. Йому відповідає максимінна стратегія, дотримуючись якої, перший гравець при будь-яких стратегіях у противника забезпечить собі виграш, який не менше
, то його називають також максиміном. Йому відповідає максимінна стратегія, дотримуючись якої, перший гравець при будь-яких стратегіях у противника забезпечить собі виграш, який не менше 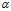 (в залежності від знака
(в залежності від знака 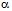 це може бути і програш, який в цьому разі виявиться мінімальним). Аналогічно визначається мінімальний програш (який може бути в дійсності і виграшем) для другого гравця:
це може бути і програш, який в цьому разі виявиться мінімальним). Аналогічно визначається мінімальний програш (який може бути в дійсності і виграшем) для другого гравця:  .
.
Величина 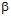 називається верхньою ціною гри або мінімаксом. Їй відповідають мінімаксні стратегії другого гравця. Має місце нерівність
називається верхньою ціною гри або мінімаксом. Їй відповідають мінімаксні стратегії другого гравця. Має місце нерівність 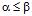 . При
. При 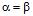 розв’язок одержується в чистих стратегіях. Для знаходження їх достатньо виділити в платіжній матриці максимінні (тобто рівні
розв’язок одержується в чистих стратегіях. Для знаходження їх достатньо виділити в платіжній матриці максимінні (тобто рівні 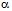 ) елементи. Будь-яка пара рядків і стовпців, на перетині яких знаходиться такий елемент, відповідає парі чистих оптимальних стратегій. При
) елементи. Будь-яка пара рядків і стовпців, на перетині яких знаходиться такий елемент, відповідає парі чистих оптимальних стратегій. При 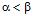 перший гравець може істотно збільшити свій середній виграш порівняно з
перший гравець може істотно збільшити свій середній виграш порівняно з  , якщо він буде користуватись не чистою (однією єдиною) стратегією, а так званою змішаною стратегією. Змішана стратегія
, якщо він буде користуватись не чистою (однією єдиною) стратегією, а так званою змішаною стратегією. Змішана стратегія 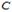 полягає в тому, що при повторі гри здійснюється випадковий вибір стратегії з деякої множини змішуваних стратегій, і для кожної змішуваної стратегії вказується імовірність її вибору.
полягає в тому, що при повторі гри здійснюється випадковий вибір стратегії з деякої множини змішуваних стратегій, і для кожної змішуваної стратегії вказується імовірність її вибору.
Отже, уможливлюючи розв’язування задач за умов невизначеності, навіть якщо неможливо знайти точний оптимальний розв’язок, математичні методи, в тому числі і методи теорії ігор, являють собою допоміжний матеріал, який дає змогу в складній ситуації оцінити кожен з можливих варіантів розвитку подій, а отже, прийняти виважене рішення.
Дата добавления: 2018-04-05; просмотров: 756; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
