Метод північно-західного кута
Виконання починається з верхньої лівої клітини (Північно-західного кута) транспортної таблиці, тобто зі змінної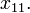 
'Крок 1. Змінній 
присвоюється максимальне значення, що допускається обмеженнями на попит і пропозицію.'
'Крок 2. Викреслюється рядок (або стовпець) з повністю реалізованою пропозицією (з задоволеним попитом). Це означає, що в викресленою рядку (стовпці) ми не будемо присвоювати значення іншим змінним (крім змінної, визначеної на першому етапі). Якщо одночасно задовольняються попит і пропозиція, викреслюється лише рядок або тільки стовпець.'
'Крок 3. Якщо не викреслено тільки один рядок або тільки один стовпець, процес зупиняється. В іншому випадку переходимо до клітини праворуч, якщо викреслять стовпець, або до клітини знизу, якщо викреслена рядок. Потім повертаємось до першого етапу.'
Наприклад для попереднього прикладу початковий опорний план буде рівним:
| 
| 
| 
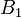
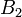
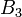
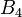
| Кількість | |
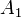
| 5 | 10 | '15' | ||
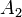
| 5 | 15 | 5 | '25' | |
| 10 | '10' | |||
| Кількість | '5' | '15' | '15' | '15' |
В даній таблиці на перетині рядка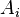 
і 
подано значення 
в початковому опорному плані (пустим клітинам відповідає значення нуль).
Рекомендації до графічного розв’язання задач ЛП
.Для розв’язування двовимірних задач лінійного програмування, тобто задач із двома змінними, а також деяких тривимірних задач застосовують графічний метод, що ґрунтується на геометричній інтерпретації та аналітичних властивостях задач лінійного програмування. Обмежене використання графічного методу зумовлене складністю побудови багатогранника розв’язків у тривимірному просторі (для задач з трьома змінними), а графічне зображення задачі з кількістю змінних більше трьох взагалі неможливе.
|
|
|
Розглянемо задачу.
Знайти
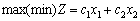(2.17)
за умов:
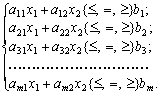(2.18)
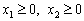. (2.19)
Припустимо, що система (2.18) за умов (2.19) сумісна і багатокутник її розв’язків обмежений.
Згідно з геометричною інтерпретацією задачі лінійного програмування (§ 2.4) кожне і-те обмеження-нерівність у (2.18) визначає півплощину з граничною прямою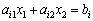 
(і = 1, 2, …, т). Системою обмежень (2.18) графічно можна зобразити спільну частину, або переріз усіх зазначених півплощин, тобто множину точок, координати яких задовольняють всі обмеження задачі — багатокутник розв’язків.
Умова (2.19) невід’ємності змінних означає, що область допустимих розв’язків задачі належить першому квадранту системи координат двовимірного простору. Цільова функція задачі лінійного програмування геометрично інтерпретується як сім’я паралельних прямих с1х1 + с2х2 = const.
Скористаємося для графічного розв’язання задачі лінійного програмування властивостями, наведеними в § 2.5:
|
|
|
якщо задача лінійного програмування має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин її багатокутника розв’язків. Якщо ж цільова функція досягає екстремального значення більш як в одній вершині багатокутника, то вона досягає його і в будь-якій точці, що є лінійною комбінацією цих вершин.
Отже, розв’язати задачу лінійного програмування графічно означає знайти таку вершину багатокутника розв’язків, у результаті підстановки координат якої в (2.17) лінійна цільова функція набуває найбільшого (найменшого) значення.
Алгоритм графічного методу розв’язування задачі лінійного програмування складається з таких кроків:
1. Будуємо прямі, рівняння яких дістаємо заміною в обмеженнях задачі (2.18) знаків нерівностей на знаки рівностей.
2. Визначаємо півплощини, що відповідають кожному обмеженню задачі.
3. Знаходимо багатокутник розв’язків задачі лінійного програмування.
4. Будуємо вектор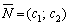 
, що задає напрям зростання значення цільової функції задачі.
5. Будуємо пряму с1х1 + с2х2 = const, перпендикулярну до вектора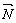 
.
6. Рухаючи пряму с1х1 + с2х2 = const в напрямку вектора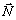 
(для задачі максимізації) або в протилежному напрямі (для задачі мінімізації), знаходимо вершину багатокутника розв’язків, де цільова функція набирає екстремального зна- чення.
|
|
|
7. Визначаємо координати точки, в якій цільова функція набирає максимального (мінімального) значення, і обчислюємо екстремальне значення цільової функції в цій точці.
У разі застосування графічного методу для розв’язування задач лінійного програмування можливі такі випадки:
1. Цільова функція набирає максимального значення в єдиній вершині А багатокутника розв’язків (рис. 2.5).
2. Максимального значення цільова функція досягає в будь-якій точці відрізка АВ (рис. 2.6). Тоді задача лінійного програмування має альтернативні оптимальні плани.
3. Задача лінійного програмування не має оптимальних планів: якщо цільова функція необмежена згори (рис. 2.7) або система обмежень задачі несумісна (рис. 2.8).
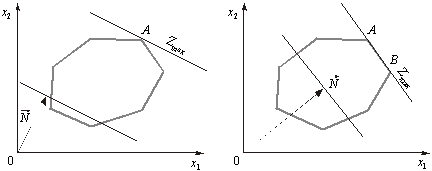
Рис. 2.5 Рис. 2.6
Рис. 2.7 Рис. 2.8
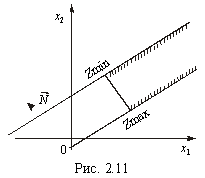
4. Задача лінійного програмування має оптимальний план за необмеженої області допустимих розв’язків (рис. 2.9 і 2.10). На рис. 2.9 у точці В маємо максимум, на рис. 2.10 у точці А — мінімум, на рис. 2.11 зображено, як у разі необмеженої області допустимих планів цільова функція може набирати максимального чи мінімального значення у будь-якій точці променя.
|
|
|
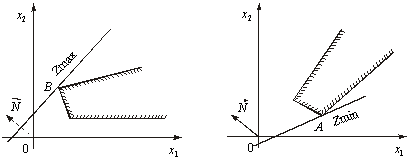
Рис. 2.9 Рис. 2.10
Розв’язувати графічним методом можна також задачі лінійного програмування n-вимірного простору, де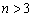 
, якщо при зведенні системи нерівностей задачі до системи рівнянь шляхом введення додаткових змінних кількість змінних n на дві більша, ніж число обмежень m, тобто 
.
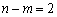Тоді, як відомо з курсу вищої математики, можна дві з n змінних, наприклад х1 та х2, вибрати як вільні, а іншіm зробити базисними і виразити через вільні. Припустимо, що це зроблено. Отримаємо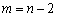 
рівнянь вигляду:
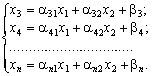
Оскільки всі значення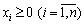 
, то мають виконуватись умови:
,
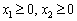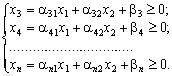(2.19.1)
Розглянемо, як можна зобразити ці умови геометрично. Візьмемо, наприклад, першу з них:
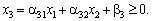
Узявши величину х3 рівною своєму крайньому значенню — нулю, отримаємо рівняння:
.
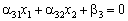Дата добавления: 2018-04-05; просмотров: 436; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!