Понятие производной сложной функции
Пусть y – сложная функция x, т.е. y = f(u), u = g(x), или
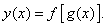
Если g(x) и f(u) – дифференцируемые функции своих аргументов соответственно в точках x и u = g(x), то сложная функция также дифференцируема в точке x и находится по формуле
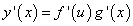
Типичная ошибка при решении задач на производные - машинальное перенесение правил дифференцирования простых функций на сложные функции. Будем учиться избегать этой ошибки.
Посмотрите на формулу 9 в таблице производных. Исходная функция является функцией от функции, причём аргумент x является аргументом лишь второй функции, а вторая функция является аргументом первой функции, или, согласно более строгому определению - промежуточным аргументом по независимой переменной x.
А теперь посмотрите на картинку ниже, которая иллюстрирует решение задач на сложные производные по аналогии с простым примером из кулинарии - приготовлении запечёных яблок, фаршированных ягодами.
Итак, "яблоко" - это функция, аргументом которой является промежуточный аргумент, а промежуточный аргумент по независимой переменной x, в свою очередь, является "фаршем" (ягодами). Представим себе, что решая задачи на производные сложной функции, сначала помещаем яблоко с фаршем в особую (физико-математическую) духовку и устанавливаем режим 1. При таком режиме духовка воздействует только на "яблоко", поскольку нужно, допустим, больше пропечь яблоко, а фарш из ягод оставить более сочным, то есть обрабатывать в другом режиме. Итак, в при режиме 1 обрабатывается яблоко, а фарш остаётся незатронутым, или, ближе к нашим задачам, находим производную функции лишь от промежуточного аргумента, то есть, "яблока". Затем в духовке устанавливается режим 2, который воздействует только на фарш, иначе говоря, записываем производную функции, являющейся промежуточным аргументом по независимой переменной x. И, в конце концов, записываем произведение производной "яблока" и производной "фарша". Можно подавать!
|
|
|
Пример 1.Найти производную функции
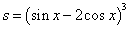
Сначала определим, где здесь "яблоко", то есть функция по промежуточному аргументу u, а где "фарш", то есть промежуточный аргумент uпо независимой переменной x. Определяем: возведение в степень - это функция по промежуточному аргументу, то есть "яблоко", а выражение в скобках (разность двух тригонометрических функций) - это промежуточный аргумент, то есть "фарш".
Тогда
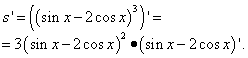
Далее по таблице производных (производная суммы или разности, производные синуса и косинуса) находим:
Искомая производная (готовое "фаршированое яблоко"):
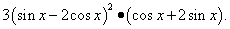
Нахождение производной сложной логарифмической функции имеет свои особенности, поэтому у нас есть и урок "Производная логарифмической функции".
|
|
|
Пример 2.Найти производную функции
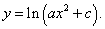
Неправильное решение: вычислять натуральный логарифм каждого слагаемого в скобках и искать сумму производных:
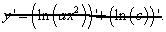
Правильное решение: опять определяем, где "яблоко", а где "фарш". Здесь натуральный логарифм от выражения в скобках - это "яблоко", то есть функция по промежуточному аргументу u, а выражение в скобках - "фарш", то есть промежуточный аргумент u по независимой переменной x.
Тогда (применяя формулу 14 из таблицы производных)
Во многих реальных задачах выражение с логарифмом бывает несколько сложнее, поэтому и есть урок "Производная логарифмической функции".
Пример 3.Найти производную функции
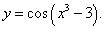
Неправильное решение:
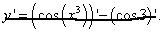
Правильное решение. В очередной раз определяем, где "яблоко", а где "фарш". Здесь косинус от выражения в скобках (формула 7 в таблице производных)- это "яблоко", оно готовится в режиме 1, воздействующем только на него, а выражение в скобках (производная степени - номер 3 в таблице производных) - это "фарш", он готовится при режиме 2, воздействующей только на него. И как всегда соединяем две производные знаком произведения. Имеем:
|
|
|
Производная сложной логарифмической функции - частое задание на контрольных работах, поэтому настоятельно рекомендуем посетить урок "Производная логарифмической функции".
Первые примеры были на сложные функции, в которых промежуточный аргумент по независимой переменной был простой функцией. Но в практических заданиях нередко требуется найти производную сложной функции, где промежуточный аргумент или сам является сложной функцией или содержит такую функцию. Что делать в таких случаях? Находить производные таких функций по таблицам и правилам дифференцирования. Когда найдена производная промежуточного аргумента, она просто подставляется в нужное место формулы. Ниже – два примера, как это делается.
Кроме того, полезно знать следующее. Если сложная функция может быть представлена в виде цепочки из трёх функций
,
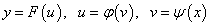то её производную следует находить как произведение производных каждой из этих функций:
.
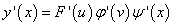Для решения многих ваших домашних заданий может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.
Нет времени вникать в решение? Можно заказать работу!
|
|
|
К началу страницы
Пройти тест по теме Производная, дифференциал и их применение
Пример 4.Найти производную функции
Применяем правило дифференцирования сложной функции, не забывая, что в полученном произведении производных промежуточный аргумент по независимой переменной x не меняется:
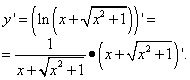
Готовим второй сомножитель произведения и применяем правило дифференцирования суммы:
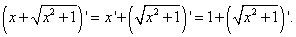
Второе слагаемое - корень, поэтому
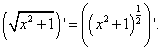
Таким образом получили, что промежуточный аргумент, являющийся суммой, в качестве одного из слагаемых содержит сложную функцию: возведение в степень - сложная функция, а то, что возводится в степень - промежуточный аргумент по независимой переменной x.
Поэтому вновь применим правило дифференцирования сложной функции:
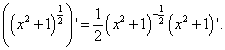
Степень первого сомножителя преобразуем в корень, а дифференцируя второй сомножитель, не забываем, что производная константы равна нулю:
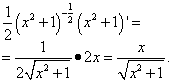
Таким образом, производная промежуточного аргумента, нужного для вычисления искомой производной сложной функции y:
Тогда
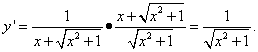
Пример 5.Найти производную функции
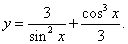
Сначала воспользуемся правилом дифференцирования суммы:
Получили сумму производных двух сложных функций. Находим первую из них:
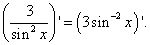
Здесь возведение синуса в степень - сложная функция, а сам синус - промежуточный аргумент по независимой переменной x. Поэтому воспользуемся правилом дифференцирования сложной функции, попутно вынося множитель за скобки:
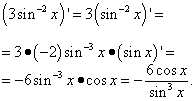
Теперь находим второе слагаемое из образующих производную искомой функции y:
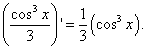
Здесь возведение косинуса в степень - сложная функция f[g(x)], а сам косинус - промежуточный аргумент по независимой переменной x. Снова воспользуемся правилом дифференцирования сложной функции:
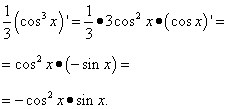
Находим искомую производную:
Таблица производных некоторых сложных функций
Для сложных функций на основании правила дифференцирования сложной функции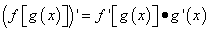 
формула производной простой функции принимает другой вид.
Дата добавления: 2018-02-28; просмотров: 331; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!