КАТУШКА С МАГНИТОПРОВОДОМ В ЦЕПИ ПЕРЕМЕННОГО ТОКА 2 страница

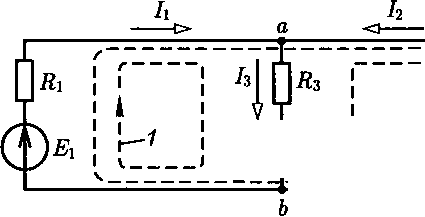
т Е и   U Jill1) и ПЪ т /Т6 Участок внешней характеристики при отрицательных значениях тока соответствует зарядке аккумулятора. Во многих случаях внутреннее сопротивление источника элект­рической энергии мало по сравнению с сопротивлением R„ и спра­ведливо неравенствоRBTI < Е. В этих случаях напряжение между выводами источника электрической энергии практически не зави­сит от тока, т. е. U&Е= const. Источник электрической энергии с малым внутренним сопротив­лением можно заменить идеализированной моделью, для которой Двт = 0. Такой идеализированный источник электрической энергии называется идеальным источником ЭДС с одним параметром Е= Ux= U.Напряжение между выводами идеального источника ЭДС не зависит от тока, а его внешняя характеристика определяет­ся выражением U=E= const,                              (1.3) которому соответствует прямая на рис. 1.9, б. Такой источник назы­вается также источником напряжения. На этом же рисунке показа­но изображение идеального источника ЭДС на схемах. В ряде специальных случаев, в частности в цепях с полупровод­никовыми приборами и электронными лампами, внутреннее сопро­тивление источника электрической энергии может быть во много раз больше сопротивления нагрузкиRn(внешней по отношению к источнику части цепи). При выполнении условияRBT>RHв таких цепях ток источника электрической энергии E/RBT= /кз = J =const, т.е. практически равен току короткого замыкания источника. Ис­точник электрической энергии с большим внутренним сопротивле­нием можно заменить идеализированной моделью, у которой RBT—> оо и Е —» оо и для которой справедливо равенствоE/RBT= J. Такой идеализированный источник электрической энергии называ­ется идеальным источником тока с одним параметромJ= 1К3. Ток источника тока не зависит от напряжения между его выводами, а его внешняя характеристика определяется выражением I=J — const,                            (1.4) которому соответствует прямая на рис. 1.9, е. На этом же рисунке дано изображение источника тока на схемах. Участок внешней ха­рактеристики с отрицательным значением напряжения соответству­ет потреблению источником тока энергии из внешней относительно него цепи. От схемы замещения источника энергии на рис. 1.8, а можно пе­рейти к эквивалентной схеме замещения с источником тока. Для этого разделим все слагаемые выражения (1.2) на внутреннее сопро­тивление источника Двт: U/ RBT= Е/ RBT— I, или Я/Двт - J = U/RBT+ J = I„ + I. Последнее равенство можно истолковать следующим образом: ток источника тока J складывается из тока I в резистивном элементеRH (во внешнем участке цепи) и тока 1ВТ в резистивном элементе с со­противлением Двт, включенном между выводами а и Ъ источника энергии (рис. 1.8, б). Отметим, что представление реальных источников электричес­кой энергии в виде двух схем замещения является эквивалентным представлением относительно внешнего участка цепи: в обоих слу­чаях одинаковы напряжения между выводами источника. Однако энергетические соотношения в двух схемах замещения не одинаковы. Не равны между собой мощности, развиваемые ис- точнико^-ЭДС (рис. 1.8, a) EI и источником тока (рис. 1.8, б) UJ, а также мощности потерьRBTI2^ Двх/вт (см. о мощности ниже, в 1.15). В теории цепей различают независимые и зависимые источники ЭДС и тока. В последнем случае источники имеют отличительное изображение на схемах, например Е(Г) (рис. 1.9, г),J( U')(рис. 1.9, Э), где Г иU' — ток и напряжение какой-либо из ветвей цепи, а их пара­метры зависят от значений других величин. 1.7. Первый и второй законы Кирхгофа Два закона Кирхгофа, называемые иногда правилами Кирхго­фа, — основные законы электрических цепей. Оба закона были ус­тановлены на основании многочисленных опытов. Согласно первому закону Кирхгофа (закону Кирхгофа для токов), алгебраическая сумма токов в любом узле электрической цепи равна нулю: Eh = О,                                     (1.5) k=1 где со знаком плюс записываются токи с положительными направ­лениями от узла, а со знаком минус — с положительными направле­ниями к узлу, или наоборот. Иначе: сумма токов, направленных от узла, равна сумме токов, направленных к узлу. Например, для узла цепи на рис. 1.10 к=1 или /3 + /5 = л + /2 + 4 Этот закон является следствием того, что в узлах цепи постоянного тока заряды не могут накапливаться. В противном слу­чае изменялись бы потенциалы узлов и токи в ветвях. (1.6) Согласно второму закону Кирхгофа (за­кону Кирхгофа для напряжений), алгебра­ическая сумма напряжений участков лю­бого контура электрической цепи равна нулю: J2uk = °> k=i   где т — число участков контура. В (1.6) со знаком плюс записываются напряжения, положитель­ные направления которых совпадают с произвольно выбранным на­правлением обхода контура, и со знаком минус — противоположно направленные, или наоборот. (1.7) В частности, для контура схемы замещения цепи, содержащего только источники ЭДС и резистивные элементы, алгебраическая сумма напряжений на резистивных элементах равна алгебраической сумме ЭДС: — Yl^k — ^Ек> к=1 к~\ к=1   где т — число резистивных элементов; п — число ЭДС в контуре. ии=Ъ Uad=u3 Рис. 1.11 В (1.7) со знаком плюс записываются ЭДС и токи, положитель­ные направления которых совпадают с произвольно выбранным на­правлением обхода контура, и со знаком минус — противоположно направлен­ные, или наоборот. Для контуров, содер­жащих источники тока, например кон­тура У, показанного штриховой линией на рис. 1.11, допустима запись второго закона Кирхгофа только в виде (1.6), но не в виде (1.7). 'л: Второй закон Кирхгофа (1.6) явля­ется следствием равенства нулю цир­куляции вектора напряженности элек­трического поля вдоль любого замкну­того контура длиной I в безвихревом поле <^Edl = 0. Например, для конту­ра 1 на рис. 1.11 по (1.6) .и1 + и2-Щ=0, 4 z k=1 3 __ \ ЛTP ____________ TP I TP i TP Рис. 1.12 = XX =~El + E2 +E3- k=1 В частном случае в контур может входить только одна ветвь цепи, так что он замыкается вне ветвей цепи (рис. 1.12). В этом случае, согласно (1.7),

RI- U — Е,

откуда

I=(U+E)/R.                             (1.8)

ГГ>

Уравнение (1.8) выражает обобщенный закон Ома для любой вет­ви с источником ЭДС (но без источников тока) с суммарными со­противлениемRи ЭДС Е или отдельного участка этой ветви с пара­метрамиRvlE.

1.8. Применение закона Ома и законов Кирхгофа для расчетов электрических цепей

В общем случае схема замещения цепи имеет В ветвей, из кото­рых Вj ветвей содержат источники тока, и У узлов.

Рассмотрим сначала расчет режима в цепи без источников тока, т.е. при В j= 0. Ее расчет сводится к нахождению токов в В ветвях. Для этого необходимо составить У — 1 независимых уравнений по первому закону Кирхгофа иК= В — У + 1 независимых уравнений по второму закону Кирхгофа. Соответствующие этим уравнениям узлы и контуры называются независимыми.

для контура 2 по (1.7) 4 ^RJk=—RJi + + h+Rsh=

Число независимых уравнений по первому закону Кирхгофа на единицу меньше числа узлов, потому что ток каждой ветви входит с разными знаками в уравнения для соединяемых ею узлов. Сумма слагаемых уравнений всех узлов тождественно равна нулю.

В качестве примера рассмотрим расчет цепи, схема замещения которой показана на рис. 1.13 и которая содержит У = 2 узла и В = 3 ветви, т. е. К = В- У+1 = 3- 2 + 1 = 2 независимых контура (1 и 2, или У и 3, или 2 и 3).

Произвольно выбираем положительные направления токов вет­вей Д, I_2f/₃. По первому закону Кирхгофа можно составить одно (У — 1 = 2 — 1 = 1) независимое уравнение, например для узла а

-Jx-J₂ +/₃ = 0                              (1.9а)

и по второму закону Кирхгофа — два (К = 2) независимых уравне­ния, например для контуров 1 и2

RJ, + R_SI_S= Е, + Е₃;                  (1.96)

R*h + Rzh = E₂ + Ez.                        (1.9в)

Решение системы трех уравнений (1.9) с тремя неизвестными тока­ми, например методом подстановок, определяет токи ветвей 1_Ь 1_Ъ 1₃.

Систему алгебраических уравнений сложной цепи, составленных на основе законов Ома и Кирхгофа, целесообразно решать числен­ными методами на ЭВМ. Например, для схемы замещения без ис­точника тока удобно воспользоваться матричной формой

AI = BE,                                 (1.10)

где А и В — квадратные матрицы коэффициентов при токах и ЭДС размером В х Д где В — число ветвей; I и Е — матрицы-столбцы не­известных токов и заданных ЭДС.

Элементы матрицы А и В являются коэффициентами в уравне­ниях (1.10) соответственно при токах и ЭДС. Отсутствие тех или иных токов и ЭДС в каких-либо уравнениях задается значениями «нуль» соответствующих элементов матриц.

Решение системы (1.10):

I = А^_1ВЕ = GE,                           (1.11а)

где

«12 а22

а1 в а2 в авв Дп Al2 Ах в

41 *21

All Al2

1_ А

А

ав1 ав2

21 J22

д

*2 в

Д21 ^22

Afil Дв2 ••Am •• Л_В2

•••AlB

(1.116)

- а_2В

»вв

— обратная матрица; А иA_ik— определит ель матрицы А и алгебраи­ческие дополнения ее элементов а,^

Gib @2В

Gn Gn (*22

Gis ^23

G = А_1В

(1.11B)

G

JB1

вв

въ

@B2 G

(1.12)

— матрица так называемых собственных С?_й и взаимных Gfc прово- димостей. Токи ветвей:

h — G_nE_x+ G_l2E₂+... + G_lBE_B\ h ⁼ G₂\E\ +G₂₂E₂+ ... + G_2BE_B\

= BE

1в — G_BlE_x+ G_B2E₂+... + G_BBE_B.

Форма записи системы уравнений (1.12) предполагает, что на­правления ЭДС и положительные направления токов в ветвях со­впадают. Так, система уравнений (1.9) в матричной форме

1	1	-1	/i		0	0	0	Ei
	0	Дз	/2	= AI =	1	0	1	E2
0	R2	Дз	/з		0	1	1	E3

У-1 { К

 

или

A		1	1	-1	-1	0	0	0	Ег
h	—	Ri	0	Rz		1	0	1	E2
h		0	R2	R3		0	1	1	E3

—R^R^ ~R\Rs

-Д2

Да

— (#2 + Д₃)

— (Rxi?2 + ВД +R^R^) — ( + Д3 ) — 0 0 0 Ei   R^Rs R2 + R3 -R3 0 0 0   1 0 1 E2 1 R1R3 —R3 Ri+ -R3 1 0 1 E2 0 1 1 Es —RlR2 R> R, 0 1 1 E3

R2 + i?3 —i?3        R2

-Д3         Ri+ Д3

Ei E2 E*

J_ R2

IGUEI(1.13)

R2         Ri       Ri+R2

определяет токи ветвей:

(1.14)

h ⁼ G_nE_x+ G_l2E₂+ G_nE₃; I2 ⁼+ G₂₂E₂+ G₂₃E₃'_y h — + G₃₂E₂+ G₃₃E₃,

^G22 ⁼(^1 +^Д3 )/ ^G33 ⁼(^1 + Щ )/

^12 — — /—G₃₁— /Д²;

^23 — ^32 - Ri / R — у/ВцК2 + + ^2^3-

Математическое обеспечение современных ЭВМ имеет стандар­тные подпрограммы решения системы алгебраических уравнений в матричной форме.

При расчете схем замещения с источниками тока возможны уп­рощения. Действительно, токи В₃ ветвей с источниками тока из­вестны. Поэтому число независимых контуров (без источников тока!), для которых необходимо составить уравнения по второму закону Кирхгофа, равноК = В - Bj- У+ 1.

С помощью законов Ома и Кирхгофа можно рассчитать режим работы любой электрической цепи. Однако порядок системы урав­нений может быть большим. Для упрощения вычислений применя­ют различные расчетные методы: контурных токов, узловых потен­циалов, межузлового напряжения, эквивалентного источника и т.д. Все эти методы основаны на законах Ома и Кирхгофа.

1.9. Метод эквивалентного преобразования схем

В ряде случаев расчет сложной электрической цепи упрощается, если в ее схеме замещения заменить группу резистивных элементов другой эквивалентной группой, в которой резистивные элементы соединены иначе. Взаимная эквивалентность заключается в том, что после замены режим работы остальной части цепи не изменится.

где =(^2 + дз )/

Смешанное соединение резистивных элементов. При наличии в цепи одного источника внешнюю по отношению к нему часть схемы можно в большинстве случаев рассматривать как смешанное (после­довательно-параллельное) соединение резистивных элементов.

Для расчета такой цепи удобно преобразовать ее схему замеще­ния в эквивалентную схему с последовательным соединением рези­стивных элементов. Например, в цепи на рис. 1.14, а между узлами а иbвключены три резистивных элемента с сопротивлениямиR₂,i2₃ и Д₄, т.е. проводимостямиG₂= 1 /Л₂,G₃= 1 /Д₃, С?₄ = 1/Д; эквива­лентная проводимость

G_}=l/i?₂ + l/ii₃+l/£₄.                          (1.15)

После замены параллельного соединения резистивных элемен­тов эквивалентным резистивным элементом с сопротивлением R₃= l/G₃получается эквивалентная схема с последовательным со­единением двух резистивных элементов Д и Д (рис. 1.14, б).

Ток в неразветвленной части

Л = и/(я_г + Д),

и токи в параллельных ветвях

(1.16)

4 ^=:U_ab/R₂; /₃ = С/_а6/Д; /₄ =U_ab/R₄,

где

U_ab = ДЛ-

Соединение резистивных элементов по схеме звезды и треу­гольника. В общем случае схему замещения цепи по схеме п-луче- вой звезды из резистивных элементов можно заменить эквивалент­ной схемой в виде n-стороннего многоугольника. Обратное преоб­разование возможно в ограниченном числе случаев. В частности, пре­образования в обоих направлениях возможны для случая треуголь­ника и трехлучевой звезды. Такое преобразование применяется при расчетах сложных цепей постоянного тока и цепей трехфазного тока (см. гл. 3).

Эквивалентность схем в виде треугольника и звезды (рис. 1.15) получается приравниванием значений сопротивлений или проводи- мостей между одноименными узлами этих схем, отсоединенных от остальной части цепи.

Найдем сопротивление между узлами А и В.

h------ 1>R\а

KE = U

©

uab

------ О-

---

Дата добавления: 2018-02-28; просмотров: 307; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!