Геометрические и физические приложения
Двойных интегралов
1. Площадь плоской фигуры D равна
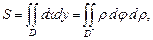 (24.9)
(24.9)
где первый интеграл вычисляется в декартовой системе координат, а второй – в полярной.
2. Объем v цилиндрического тела V (рис. 24.16), ограниченного сверху поверхностью 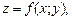 находят по формуле
находят по формуле
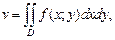 (24.10)
(24.10)
где D – основание криволинейного цилиндра, а его образующие параллельны оси Oz.
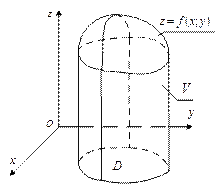
Рис. 24.16
3. Для нахождения площади ограниченной части поверхности, заданной уравнением 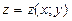 и имеющей проекцию
и имеющей проекцию 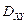 на плоскость xOy, применяют формулу
на плоскость xOy, применяют формулу
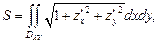 (24.11)
(24.11)
где 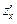 и
и  – непрерывные в области
– непрерывные в области 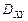 функции.
функции.
4. Если f (x; y) – непрерывная функция, выражающая поверхностную плотность распределения массы по плоской пластине D, то масса m этой плоской пластины вычисляется по формуле
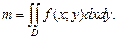 (24.12)
(24.12)
5. Для нахождения координат центра масс плоской материальной пластины D c поверхностной плотностью распределения массы, выражаемой функцией f (x; y), применяют следующие формулы:
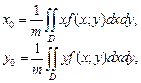 (24.13)
(24.13)
где m – масса пластины D, вычисляемая по формуле (24.12).
Пример 1. Найти площадь области D, ограниченной указанными кривыми:
1) 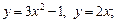 2)
2) 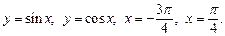
Решение. 1) Изобразим область D (рис. 24.17).
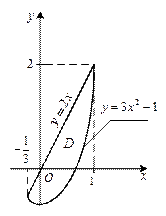 Рис. 24.17
Рис. 24.17
| Она является правильной в направлении оси Oy. Найдем точки пересечения двух графиков, чтобы найти проекцию области на ось Ox:
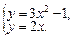 Получаем:
Получаем: 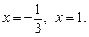 Найдем границы изменения координат интегрирования:
Найдем границы изменения координат интегрирования: 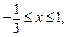 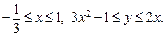 Вычислим площадь области D по формуле (24.9)
Вычислим площадь области D по формуле (24.9)
|
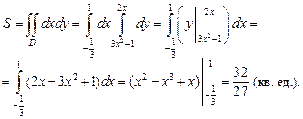
2) Изобразим область интегрирования D (рис. 24.18).
|
|
|
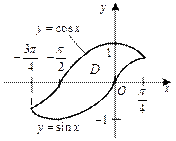 Рис. 24.18
Рис. 24.18
| Она является правильной в направлении оси Oy. Найдем точки пересечения двух графиков, ограничивающих область интегрирования, и определим границы изменения координат интегрирования:
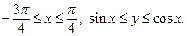 Вычислим площадь области D по формуле (24.9):
Вычислим площадь области D по формуле (24.9):
|
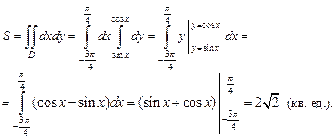
Пример 2. Найти площадь области D, ограниченной указанными кривыми, используя полярные координаты:
1)  (трехлепестковая роза);
(трехлепестковая роза);
2) 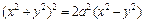 (лемниската Бернулли).
(лемниската Бернулли).
Решение. 1) Изобразим шестую часть области интегрирования D (рис. 24.19).
 Рис. 24.19
Рис. 24.19
| Используем симметрию заданной области. Определим границы изменения переменных интегрирования (с учетом того, что мы рассматриваем шестую часть искомой площади):
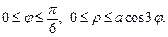
|
Вычислим площадь области D по формуле (24.9), перейдя к полярным координатам:
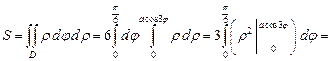
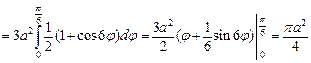 (кв. ед.).
(кв. ед.).
2) Запишем уравнение лемнискаты Бернулли в полярных координатах: 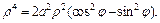 откуда
откуда 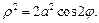 Окончательно имеем:
Окончательно имеем: 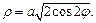
Изобразим четвертую часть области интегрирования D (рис. 24.20).
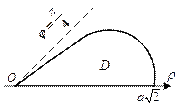 Рис. 24.20
Рис. 24.20
| Используем симметричность области интегрирования. С учетом того, что мы рассматриваем четвертую часть искомой площади, определим границы изменения переменных интегрирования:
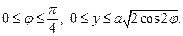
|
Вычислим площадь области D по формуле (24.9)
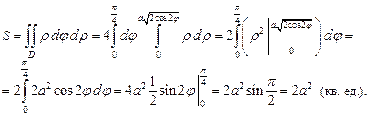
Пример 3. Используя двойной интеграл, вычислить объем тела, ограниченного указанными поверхностями:
|
|
|
1) 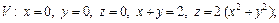
2) 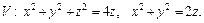
Решение. 1) Изобразим тело V (рис. 24.21), объем которого необходимо найти, и спроектируем его на плоскость xOy.
При этом мы получим плоскую область 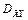 (рис. 24.22).
(рис. 24.22).
Определим границы интегрирования, исходя из области 

Применив формулу (24.10), получим:
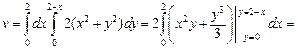
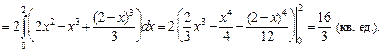
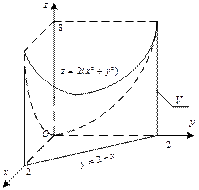 Рис. 24.21
Рис. 24.21
| 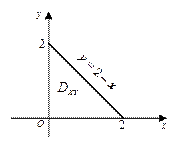 Рис. 24.22
Рис. 24.22
|
2) Найдем пересечение сферы с центром в точке (0; 0; 2) радиуса 2 и кругового параболоида, ограничивающих тело V: 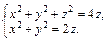 Следовательно,
Следовательно, 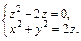 Окончательно имеем:
Окончательно имеем: 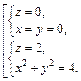
Изобразим указанное тело V (рис. 24.23).
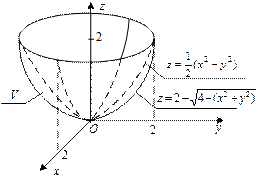
Рис. 24.23
Его проекцией 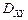 на плоскость xOy будет являться круг с центром в начале координат радиуса 2. Запишем уравнение окружности
на плоскость xOy будет являться круг с центром в начале координат радиуса 2. Запишем уравнение окружности 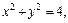 ограничивающей область интегрирования
ограничивающей область интегрирования 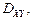 в полярных координатах:
в полярных координатах: 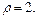 Используем симметричность области
Используем симметричность области 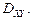 Для ее четвертой части определим границы интегрирования в полярных координатах:
Для ее четвертой части определим границы интегрирования в полярных координатах:
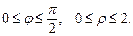
Выразим подынтегральные функции через полярные координаты, для чего используем формулы перехода (24.4). Получим уравнения: кругового параболоида 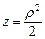 и сферы
и сферы 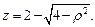
Вычисляем объем тела V по формуле (24.10), представив это тело как разность между двумя криволинейными цилиндрами, один из которых ограничен сверху параболоидом, а другой – сферой:
|
|
|
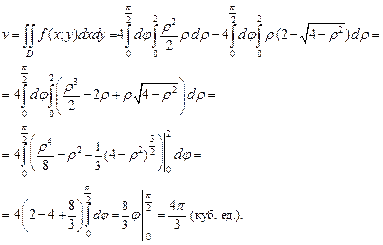
Пример 4. Вычислить площадь поверхности  при условии, что
при условии, что 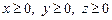 .
.
Решение. Изобразим часть плоскости 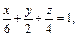 лежащую в первом октанте, как того требует условие задачи (рис. 24.24).
лежащую в первом октанте, как того требует условие задачи (рис. 24.24).
Вычислим элемент площади по формуле 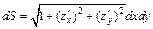 (см. соотношение 24.11).
(см. соотношение 24.11).

Рис. 24.24
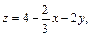 а потому элемент площади будет иметь вид:
а потому элемент площади будет иметь вид:
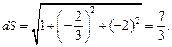
Спроектируем поверхность, площадь которой необходимо найти, на одну из координатных плоскостей (в данном случае – на плоскость xOy) и получим плоскую область 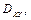 ограниченную прямыми
ограниченную прямыми 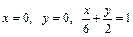 (рис. 24.25).
(рис. 24.25).
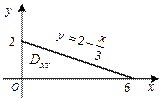 Рис. 24.25
Рис. 24.25
| Определим границы изменения координат x и y, ориентируясь на область интегрирования 
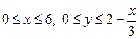 .
Вычислим искомую площадь поверхности S по формуле (24.11): .
Вычислим искомую площадь поверхности S по формуле (24.11):
|
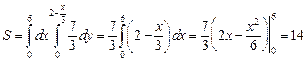 (кв. ед.).
(кв. ед.).
Пример 5. Вычислить площадь части кругового параболоида 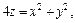 вырезаемого цилиндром
вырезаемого цилиндром 
Решение. Изобразим указанную поверхность (рис. 24.26).
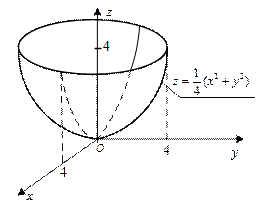
Рис. 24.26
Ее проекцией на плоскость xOy будет круг. Найдем уравнение линии пересечения параболоида и цилиндра, ограничивающей этот круг: 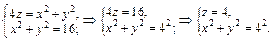
Таким образом, видим, что поверхность проектируется на круг 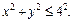 Вычислим значение выражения
Вычислим значение выражения 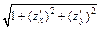 из формулы (24.11).
из формулы (24.11).
В нашем случае: 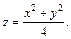 Следовательно,
Следовательно, 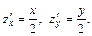 Итак, выражение имеет вид:
Итак, выражение имеет вид:
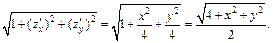
Вычислим искомую площадь поверхности по формуле (24.11), перейдя в двойном интеграле к полярным координатам по формулам (24.4):
|
|
|
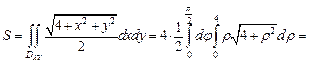
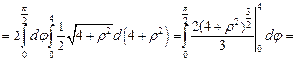
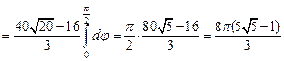 (кв.ед.).
(кв.ед.).
Пример 6. Найти массу плоской пластины D, ограниченной линиями 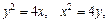 если плотность распределения массы на пластине
если плотность распределения массы на пластине 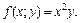
Решение. Изобразим пластину D (рис. 24.27).
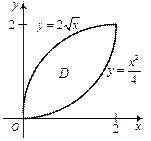 Рис. 24.27
Рис. 24.27
| Расставим пределы интегрирования, исходя из рисунка области D: 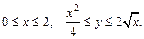 Найдем массу этой пластины по формуле (24.12): Найдем массу этой пластины по формуле (24.12):
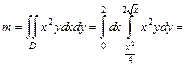
|
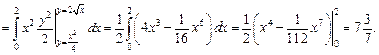
Пример 7. Найти координаты центра масс плоской однородной пластины D, ограниченной линиями 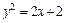 и
и 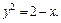
Решение. Изобразим пластину D (рис. 24.28).
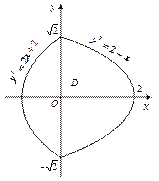 Рис. 24.28
Рис. 24.28
| В уравнениях кривых, ограничивающих указанную область, выразим x через y, поскольку область является элементарной в направлении оси Ox. Из первого уравнения имеем: 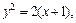 т. е. т. е. 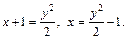 Из второго уравнения линии получаем: Из второго уравнения линии получаем: 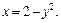 Определим границы изменения переменной y:
Определим границы изменения переменной y: 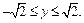 Учитывая симметричность отрезка изменения y, будем считать, что Учитывая симметричность отрезка изменения y, будем считать, что 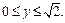
|
Найдем массу этой пластины по формуле (24.12):
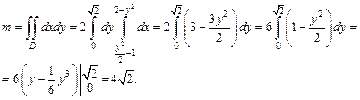
Воспользуемся формулами (24.13) и вычислим сначала абсциссу, а затем и ординату центра масс пластины:
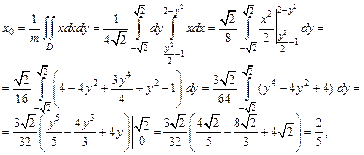
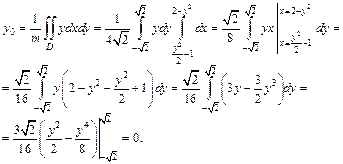
Таким образом, точка 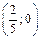 – центр масс данной пластины.
– центр масс данной пластины.
Задания
I уровень
1.1. Найдите площадь области D, ограниченной указанными кривыми:
1) 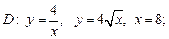 2)
2) 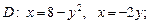
3) 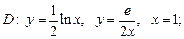 4)
4) 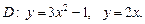
1.2. Используя двойные интегралы, вычислите объем тела, ограниченного указанными поверхностями:
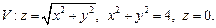
1.3. Вычислите площадь поверхности, ограниченной указанными кривыми:
1) 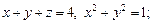
2) 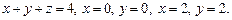
1.4. Найдите массу плоской пластины, ограниченной указанными кривыми при заданной плотности распределения f (x; y):
1) 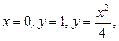

2) 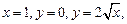
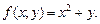
II уровень
2.1. Найдите площадь области D, ограниченной указанными кривыми:
1) 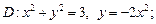
2) 
3) 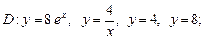
4) 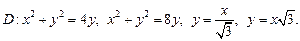
2.2. Используя двойные интегралы, вычислите объем тела, ограниченного указанными поверхностями:
1) 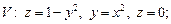
2) 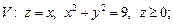
3) 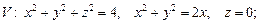
4) 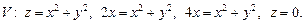
2.3. Вычислите площадь поверхности, ограниченной сферой 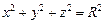 и цилиндром
и цилиндром 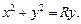
2.4. Найдите массу плоской пластины, ограниченной указанными кривыми при указанных условиях, если известна поверхностная плотность распределения массы f (x; y):
1) 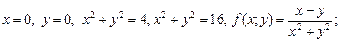
2) 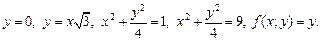
2.5. Найдите координаты центра масс однородной плоской пластины D, ограниченной одной полуволной косинусоиды 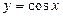 и осью абсцисс.
и осью абсцисс.
III уровень
3.1. Найдите площадь области D, ограниченной указанными кривыми.
1) 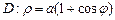 –кардиоида;
–кардиоида;
2) 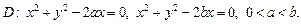
3.2. Используя двойные интегралы, вычислите объем тела, ограниченного указанными поверхностями:
1) 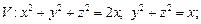 2)
2) 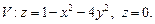
3.3. Найдите площадь поверхности части сферы 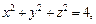 вырезанной цилиндром
вырезанной цилиндром 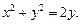
3.4. Найдите массу плоской пластины, ограниченной указанными кривыми при указанных условиях, если известна поверхностная плотность распределения массы f (x; y):
1) 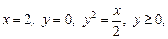
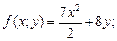
2) 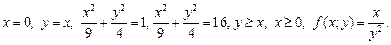
3.5. Найдите координаты центра масс однородной плоской пластины D, ограниченной линиями  и
и 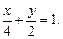
Дата добавления: 2015-12-17; просмотров: 23; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
