В полярной системе координат
Если область интегрирования представляет собой круг или его часть, для упрощения производимых вычислений переходят к полярным координатам. Формулы перехода от декартовых координат x и y к полярным координатам 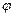 и
и 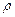 имеют вид:
имеют вид:
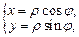 (24.4)
(24.4)
где 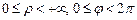 (или
(или 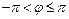 ).
).
Формула замены переменных в двойном интеграле при переходе к полярным координатам имеет вид:
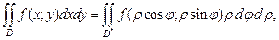 (24.5)
(24.5)
где 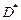 – область в полярной системе координат, соответствующая области D в декартовой системе координат;
– область в полярной системе координат, соответствующая области D в декартовой системе координат;
f (x; y) – функция, непрерывная в этой области.
Для вычисления двойного интеграла в полярных координатах также переходят к повторному интегралу. При этом используют понятие области, правильной в полярной системе.
Область D называют правильной в полярной системе, если всякий луч, выходящий из полюса и проходящий через внутреннюю точку области, пересекает только одну (только один раз) «линию входа» и только одну (только один раз) «линию выхода».
В случае правильной области (рис. 24.12) верна формула
 (24.6)
(24.6)
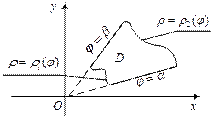 Рис. 24.12
Рис. 24.12
| Если область интегрирования D ограничена эллипсом 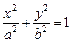 или его частью, обосновано применение обобщенных полярных координат, переход к которым осуществляется по формулам: или его частью, обосновано применение обобщенных полярных координат, переход к которым осуществляется по формулам:
|
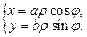 (24.7)
(24.7)
Тогда
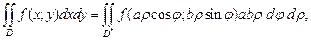 (24.8)
(24.8)
где 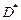 – область в обобщенной полярной системе координат, соответствующая области D в декартовой системе координат.
– область в обобщенной полярной системе координат, соответствующая области D в декартовой системе координат.
Далее переходят к повторному интегралу.
Пример 1. Вычислить двойной интеграл по области D, ограниченной указанными линиями, используя полярные координаты:
|
|
|
1) 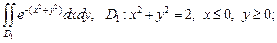
2) 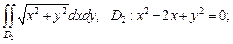
3) 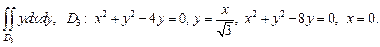
Решение. 1) Прежде, чем вычислять интеграл, изобразим область интегрирования  (рис. 24.13).
(рис. 24.13).
 Рис. 24.13
Рис. 24.13
| В полярной системе координат Op уравнение окружности  ограничивающей область ограничивающей область 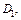 имеет вид: имеет вид: 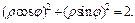 т. е. т. е. 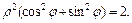 Окончательно получаем, что Окончательно получаем, что 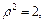 откуда откуда 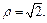 Определим границы изменения координат Определим границы изменения координат 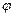 и и 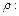 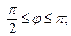 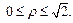
|
Область 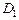 является правильной в полярной системе координат. Поэтому, воспользовавшись формулами (24.4) и (24.5) перехода от декартовых координат к полярным, перейдем к повторному интегралу по формуле (24.6):
является правильной в полярной системе координат. Поэтому, воспользовавшись формулами (24.4) и (24.5) перехода от декартовых координат к полярным, перейдем к повторному интегралу по формуле (24.6):
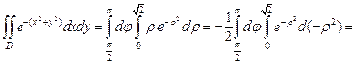
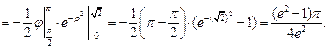
2) Изобразим область интегрирования 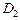 (рис. 24.14).
(рис. 24.14).
 Рис. 24.14
Рис. 24.14
| Воспользуемся формулами (24.4) перехода от декартовых координат к полярным координатам. В новой системе координат Op уравнение заданной окружности 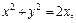 ограничивающей область ограничивающей область 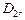 принимает вид: принимает вид: 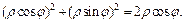 После сокращения имеем После сокращения имеем 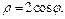 Определим границы изменения координат
Определим границы изменения координат 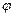 и и 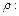
|

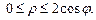
Воспользуемся формулой (24.6) перехода от двойного интеграла к повторному и вычислим его:
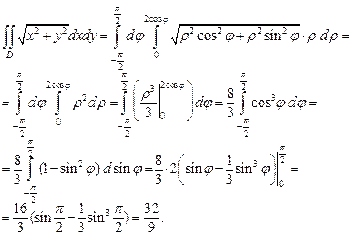
3) Изобразим область интегрирования  (рис. 24.15).
(рис. 24.15).
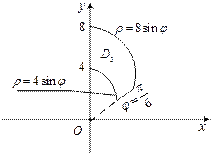 Рис. 24.15
Рис. 24.15
| Воспользуемся формулами (24.4) перехода от декартовых координат к полярным координатам. В новой системе координат Op уравнение заданной окружности 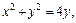 ограничивающей область ограничивающей область 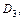 имеет вид: имеет вид: 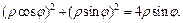 Откуда Откуда  и окончательно и окончательно 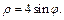
|
Уравнение окружности 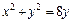 в новой системе координат будет следующим:
в новой системе координат будет следующим: 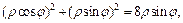 т. е.
т. е.  или
или 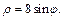
|
|
|
Область 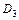 является правильной, ее ограничивают линии
является правильной, ее ограничивают линии 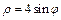 и
и 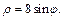
Прямая 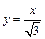 имеет угловой коэффициент
имеет угловой коэффициент 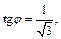 откуда находим уравнение луча
откуда находим уравнение луча 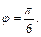 Для уравнения прямой
Для уравнения прямой 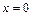 имеем
имеем 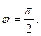 Значит, границы изменения координат
Значит, границы изменения координат 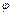 и
и 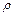 таковы:
таковы:
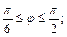
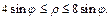
Перейдя к повторному интегралу по формуле (24.6), вычислим его:
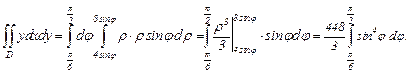
Для вычисления определенного интеграла воспользуемся формулами понижения степени: 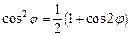 и
и 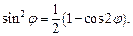
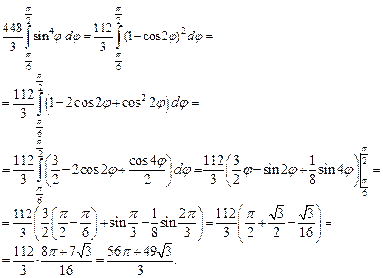
Задания
I уровень
1.1. Вычислите двойной интеграл по области D, ограниченной указанными линиями, используя полярные координаты:
1) 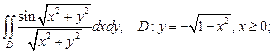
2) 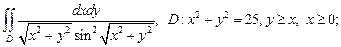
3) 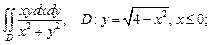
4) 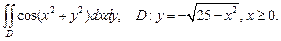
II уровень
2.1. Вычислите двойной интеграл по области D, ограниченной указанными линиями, используя полярные координаты:
1) 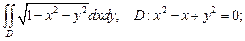
2) 
3) 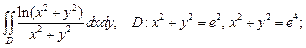
4) 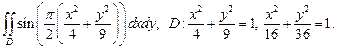
III уровень
3.1. Вычислите двойной интеграл по области D, ограниченной указанными линиями, используя полярные координаты:
1) 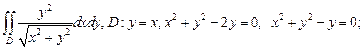
2) 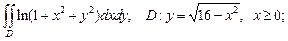
3) 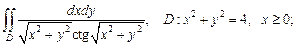
4) 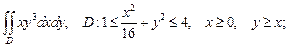
5) 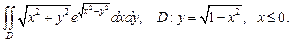
Дата добавления: 2015-12-17; просмотров: 24; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
