Тогда при таком допущении из (3.7) следует
Институт геологии и нефтегазодобычи
Кафедра геологии месторождений нефти и газа
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Методические указания
для лабораторных и самостоятельных занятий
студентов специальности 130304.65 «Геология нефти и газа» и
по направлению 230400 «Информационные системы и технологии»
для всех форм обучения
(Часть первая)
Составитель: В. А. Белкина
Тюмень
ТюмГНГУ
УДК 519.95
Вычислительная математика: метод. указ. для студентов, обучающихся по специальности 130304.65 «Геология нефти и газа» и по направлению 230400 «Информационные системы и технологии» для всех форм обучения / сост. В.А.Белкина; Тюменский государственный нефтегазовый университет.– 2-е изд., испр.– Тюмень: Издательский центр БИК ТюмГНГУ 2012.– 32 с.
Методические указания для лабораторных и самостоятельных занятий рассмотрены и рекомендованы к изданию методическим семинаром кафедры геологии месторождений нефти и газа
«16» февраля 2012 года, протокол № 7.
Аннотация
Методические указания и индивидуальные задания по дисциплине «Вычислительная математика» предназначены для студентов, обучающихся по специальности 130304.65 «Геология нефти и газа» и по направлению 230400 «Информационные системы и технологии». Данная дисциплина изучается в одном семестре.
Приведено содержание основных тем дисциплины, указаны перечень лабораторных и самостоятельных работ. Приведены варианты заданий для индивидуальных работ. Даны методические указания по выполнению лабораторных и самостоятельных работ.
|
|
|
1. ВВЕДЕНИЕ
Построение геологических моделей основано на большом числе эмпирических (полевых) данных, которые являются приближенными, т.к. содержат ошибки измерений. Эти погрешности называют начальными.
Анализ алгоритмов, используемых при построении моделей, показывает, что многие из них при определенных ситуациях оказываются неустойчивыми. Погрешности, возникающие при этом, называют алгоритмическими. Это означает, что результаты их применения содержат ошибки, которые можно было бы значительно уменьшить при более обоснованном выборе алгоритмов. Указанная проблема в последнее время становится все более острой в связи с появлением на рынке большого числа программных приложений (GST, Isoline, Petrel, LandMark, Tigress, ROXAR и т.д.), каждый из которых предоставляет пользователю большие возможности выбора алгоритмов на каждом этапе геологической интерпретации. В связи с этим при подготовке инженеров-геологов специальности 130304.65 «Геология нефти и газа» и инженеров по направлению 230400 «Информационные системы и технологии» ведется курс «Вычислительной математики».
|
|
|
Глубокое освоение методов этого курса даёт основу понимания вычислительной сложности алгоритмов, используемых при построении моделей. Использование этих знаний позволит свести к возможному минимуму ошибки полученных геологических моделей.
В настоящем методическом указании рассматриваются такие разделы вычислительной математики, как теория погрешностей, элементы линейной алгебры.
2. ПРАВИЛА ТЕХНИКИ БЕЗОПАСНОСТИ ПРИ ПРОВЕДЕНИИ
ЛАБОРАТОРНЫХ И САМОСТОЯТЕЛЬНЫХ РАБОТ
Оборудование. Лабораторные и самостоятельные работы выполняются на персональных компьютерах в среде программного комплекса Excel.
К выполнению лабораторных и самостоятельных работ допускаются студенты, изучившие настоящие правила по технике безопасной работы на ПК, а также прошедшие инструктаж по технике безопасности на рабочем месте.
Во время работы в компьютерном классе запрещается:
- включать без разрешения оборудование;
- трогать разъемы соединительных кабелей и проводов (возможно поражение электрическим током);
- прикасаться к питающим проводам и устройствам заземления;
- прикасаться к экрану и к тыльной стороне монитора, клавиатуры;
|
|
|
- включать и выключать аппаратуру без указания преподавателя;
- работать в верхней одежде и влажными руками;
- находиться во время перемены в компьютерном классе без разрешения преподавателя;
- класть диски, книги, тетради и другие предметы на монитор и клавиатуру;
- устанавливать или копировать программы с дискет, дисков и флеш-носителей на компьютер, предварительно не проверив их антивирусом.
Во время работы в компьютерном классе:
- следите за исправностью аппаратуры и немедленно прекращайте работу при появлении необычного звука или самопроизвольного отключения аппаратуры;
- легко и быстро нажимайте на клавиши, не допуская резких ударов;
- не пользуйтесь клавиатурой и мышью, если не включен компьютер;
- работайте на клавиатуре чистыми руками;
- не пытайтесь самостоятельно устранить неисправность аппаратуры;
- при появлении запаха гари немедленно прекратите работу, выключите аппаратуру и сообщите об этом преподавателю.
3. ТЕОРИЯ ПОГРЕШНОСТЕЙ
3.1. Цель работы
Овладеть навыками оценки погрешности приближённых величин и сравнения замеров по точности.
3.2. Основные теоретические положения
В основе геологической науки, как и многих других естественных наук, лежат измерения. Действительно, данные о численных значениях геологических параметров находятся с помощью измерений.
|
|
|
Под измерением понимается определение значения какой-либо величины с применением технических средств – измерительных приборов. Различают два вида измерений геолого-физических параметров – прямые и косвенные. При прямом измерении значение искомой величины определяется непосредственно с помощью прибора. При косвенном измерении значение искомого геологического параметра находят, основываясь на результатах прямых измерений других геолого-физических параметров, с которыми эта величина связана известной зависимостью. Например, значение коэффициента проницаемости (Кпр) можно определить, пользуясь результатами либо гидродинамических испытаний, либо каротажными данными. Отметим, что значения Кпр, полученные этими методами, могут отличаться существенно.
Особенностью измерения является принципиальная невозможность получения результатов, в точности равных истинному значению измеряемой величины. Это приводит к необходимости оценивать степень близости результатов измерения к истинному значению, т.е. оценивать погрешность измерения.
Погрешности измерений зависят от многих причин. По их характеру различают систематические, случайные и грубые (промахи) погрешности.
Систематические погрешности связаны либо с точностью прибора, либо метода измерений, либо с невозможностью учета некоторых факторов. Вернемся к упомянутому примеру оценки Кпр.
При проведении гидродинамических испытаний оценка Кпр в большинстве случаев получается заметно заниженной вследствие загрязненности (кольматации) призабойной зоны при бурении. Если причины, вызывающие систематические погрешности, известны, то эти погрешности, в принципе, могут быть исключены введением поправок, хотя на практике этого не всегда легко добиться.
Случайные погрешности вызываются большим числом случайных факторов, действие которых на каждое отдельное измерение различно и не может быть заранее учтено. Например, они могут вызываться локальными изменениями электрических и магнитных полей, колебаниями давления и температуры, изменением геохимических факторов и т.д. Хотя исключить случайные погрешности отдельных измерений невозможно, можно уменьшить их влияние на окончательный результат, увеличив число измерений.
Грубые погрешности возникают в результате просчёта, неправильной корреляции и т.д. Результаты расчётов на основе измерений, содержащих грубые ошибки, существенно отличаются от других и поэтому могут быть замечены при тщательном анализе модели. Их обычно исключают.
В разделе «Теория погрешностей» изучается влияние начальных погрешностей на погрешности косвенных измерений, полученных математическими преобразованиями.
Приближенным числом 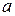 называется число, незначительно отличающееся от точного числа
называется число, незначительно отличающееся от точного числа 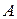 и заменяющее его в вычислениях.
и заменяющее его в вычислениях.
Ошибкой или погрешностью 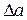 приближенного числа
приближенного числа 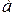 называется разность между точным числом
называется разность между точным числом 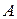 и его приближением:
и его приближением:
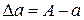
На практике чаще пользуются абсолютной погрешностью приближенного числа:
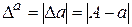 . (3.1)
. (3.1)
Как правило, число 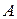 не известно и, следовательно, нельзя определить
не известно и, следовательно, нельзя определить 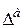 по формуле (3.1). В этом случае используют оценку её сверху.
по формуле (3.1). В этом случае используют оценку её сверху.
Предельной абсолютной погрешностью 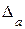 приближения
приближения 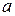 называется всякое число, не меньшее абсолютной погрешности этого числа:
называется всякое число, не меньшее абсолютной погрешности этого числа:
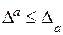 . (3.2)
. (3.2)
Естественно, из разных оценок 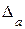 выбирают наименьшую возможную.
выбирают наименьшую возможную.
Из (3.2) следует интервал для точного числа 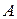 :
:
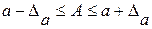 . (3.3)
. (3.3)
Понятия абсолютной погрешности (или 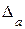 ) недостаточно при решении задачи сравнения точности двух измерений, особенно в случае сравнения точности измерений, имеющих различные единицы измерения. Например, требуется выяснить какой из двух параметров: объем геологического нефтенасыщенного тела (V) или коэффициент пористости (Кп) вносит большую погрешность в значение балансовых запасов нефти. Решение этой задачи возможно только на основании понятия относительной погрешности.
) недостаточно при решении задачи сравнения точности двух измерений, особенно в случае сравнения точности измерений, имеющих различные единицы измерения. Например, требуется выяснить какой из двух параметров: объем геологического нефтенасыщенного тела (V) или коэффициент пористости (Кп) вносит большую погрешность в значение балансовых запасов нефти. Решение этой задачи возможно только на основании понятия относительной погрешности.
Относительной погрешностью 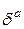 приближения
приближения 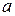 называется отношение абсолютной погрешности
называется отношение абсолютной погрешности  этого числа к модулю соответствующего точного числа
этого числа к модулю соответствующего точного числа 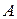
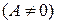 :
:
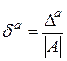 .
.
Отсюда  .
.
Предельной относительной погрешностью 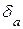 приближения
приближения 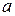 называется всякое число, не меньшее относительной погрешности этого числа:
называется всякое число, не меньшее относительной погрешности этого числа: 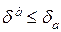 , т.е.
, т.е. 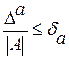 , отсюда
, отсюда 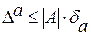 . Таким образом, за
. Таким образом, за  можно принять:
можно принять: 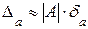 . Так как на практике А - неизвестно и А» а, то вместо этой формулы используют
. Так как на практике А - неизвестно и А» а, то вместо этой формулы используют 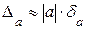 . Зная
. Зная 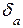 и используя формулу (3.3), напишем интервал точного числа А через предельную относительную погрешность:
и используя формулу (3.3), напишем интервал точного числа А через предельную относительную погрешность:
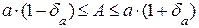 . (3.4)
. (3.4)
К оценке точности приближения а можно подойти с другой стороны через понятие числа верных знаков. Известно, что всякое положительное число а может быть представлено в виде
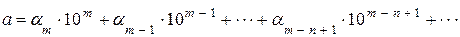 , (3.5)
, (3.5)
где 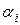 – цифры числа а, причем старшая цифра
– цифры числа а, причем старшая цифра 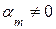 , а m – некоторое целое число (старший десятичный разряд числа а).
, а m – некоторое целое число (старший десятичный разряд числа а).
Значащей цифрой приближенного числа называется всякая цифра в его десятичном изображении, отличная от нуля, и нуль, если он содержится между значащими цифрами или является сохраненным десятичным знаком.
Говорят, что n первых значащих цифр приближенного числа а являются верными, если абсолютная погрешность этого числа не превышает половины единицы разряда, выражаемого n -ой значащей цифрой, считая слева направо.
Таким образом, если для приближенного числа а, заменяющего точное число А, известно, что
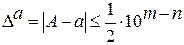 , (3.6)
, (3.6)
то по определению, первые n цифр 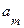 ,
, 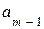 ,
, 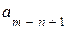 этого числа верные.
этого числа верные.
Естественно, что между двумя рассмотренными подходами существует связь, которая выражается теоремой. Эта теорема связывает величину относительной погрешности приближенного числа с количеством верных знаков этого числа.
Теорема. Если положительное приближенное число а имеет n верных десятичных знаков, то относительная погрешность 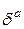 этого числа не превосходит
этого числа не превосходит 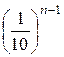 , делённую на первую значащую цифру данного числа, т.е.
, делённую на первую значащую цифру данного числа, т.е.
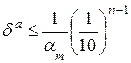 ,
,
где 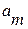 - первая значащая цифра числа а.
- первая значащая цифра числа а.
В теории погрешностей существует ряд теорем, позволяющих определить погрешность чисел, полученных различными арифметическими действиями над приближенными числами. Приведем некоторые формулы для подсчета абсолютной и относительной погрешностей косвенных измерений (табл. 3.1).
Таблица 3.1
| Математическая операция | Абсолютная погрешность | Относительная погрешность |
| Х=А+В+С | DХ=DА+DВ+DС | 
|
| Х=А - В | DХ=DА+DВ | 
|
| Х=А×В×С | DХ=В×С×DА+А×С×DВ+А×В×DС | 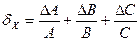
|

| DХ = 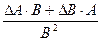
| 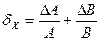
|
| Х=Аn | DХ=n×Аn-1×DА | 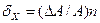
|
Рассмотрим общую формулу для погрешностей косвенных измерений, которая заключается в следующем: известны погрешности аргументов некоторой функции  , требуется определить погрешность этой функции.
, требуется определить погрешность этой функции.
Пусть задана дифференцируемая функция 
и пусть известны 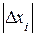 ,
,  - абсолютные погрешности аргументов. Тогда предельная абсолютная погрешность функции
- абсолютные погрешности аргументов. Тогда предельная абсолютная погрешность функции
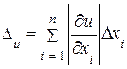 . (3.7)
. (3.7)
Разделив обе части равенства (3.7) на u, получим предельную относительную погрешность функции u:
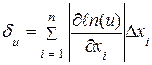 . (3.8)
. (3.8)
На практике важна также обратная задача: каковы должны быть абсолютные погрешности аргументов функции, обеспечивающие вычисление функции u с погрешностью 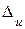 , не превышающей заданной величины. Эта задача математически не корректна, так как имеет бесчисленное множество решений.
, не превышающей заданной величины. Эта задача математически не корректна, так как имеет бесчисленное множество решений.
Задача становится корректной, т.е. имеет единственное решение, при допущении так называемого принципа равных влияний. Согласно этому принципу, все частные дифференциалы
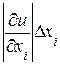 ,
, 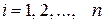
вносят примерно одинаковый вклад в абсолютную погрешность 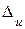 функции
функции 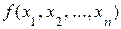 :
:
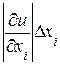 »
» 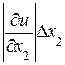 » ….»
» ….» 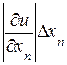 »
» 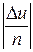 .
.
Тогда при таком допущении из (3.7) следует
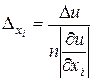 .
. 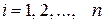 (3.9)
(3.9)
Отметим, что влияние ошибок измерений на результат в некоторых ситуациях целесообразнее изучать методами математической статистики.
Следует иметь в виду, что в полевых данных особо тщательно должны анализироваться систематические погрешности, здесь имеются в виду случаи, когда все измерения или только меньше, или только больше соответствующего точного числа. Это обстоятельство может быть обусловлено, в частности, особенностями методики измерения.
Для наглядности рассмотрим оценку пористости газо-, водо- и керосинонасыщением для различных типов пород. Метод газонасыщения по своей физической основе точнее методов насыщения жидкостью, так как газ, имея меньший размер молекул и меньшую вязкость по сравнению с жидкостью, может пройти в самые тонкие поры горной породы. То же самое можно сказать про водо- и керосинонасыщение. Вода более активная в связи с её полярностью и меньшим размером молекул. Отсюда следует, что пористость, установленная по газо- или водонасыщению в отдельных случаях может оказаться выше пористости, определенной по насыщению керосином. Это особенно актуально для крепко сцементированных песчано-алевролитовых и алевролитовых пород с большим количеством цемента, характеризующихся наличием тонких пор. При измерении открытой пористости таких пород метод керосинонасыщения даёт систематическую ошибку, величина которой колеблется от 2% до 7-9%.
Варианты заданий
№ 1 № 2
1)  =6,63; 19/41=0,463. 1)7/15=0,467;
=6,63; 19/41=0,463. 1)7/15=0,467; 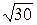 =5,48.
=5,48.
2) а) 22,553 (±0,016); 2) а) 17,2834; d=0,3%;
б) 2,8546; d=0,3%. б) 6,4257 (±0,0024).
3) х=37,1 Dх=0,3 3) х=12,7 Dх=0,1
у=9,87 Dу=0,11 у=8,1 Dу=0,09 
z=6,052 Dz=0,016. z=4,7 Dz=0,071.
4) х1=2,10415 4) х1=3,10815
x2=1,93521 x2=1,17516
х3=0,84542. х3=0,75112.
№ 3 № 4
1) 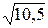 =3,24; 4/17=0,235. 1)15/7=2,14;
=3,24; 4/17=0,235. 1)15/7=2,14; 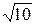 =3,16.
=3,16.
2) а) 34,834; d=0,1% 2) а) 2,3485 (±0,0042);
б) 0,5748 (±0,0034). б) 0,34484; d=0,4%.
3) х=47,6 Dх=0,41 3) х=48,3 Dх=0,39
у=6,81 Dу=0,12 у=7,53 Dу=0,15 
z=3,971 Dz=0,014. z=1,786 Dz=0,016.
4) х1=7,85169 4) х1=9,15176
x2=1,17972 x2=1,18186
х3=0,75413. х3=0,85176.
№ 5 № 6
1) 6/7=0,857; 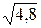 =2,19. 1)12/11=1,091;
=2,19. 1)12/11=1,091;  =2,61.
=2,61.
2) а) 5,435 (±0,0028); 2) а) 8,24163; d=0,2%;
б) 10,8441; d=0,5%. б) 0,12356 (±0,00036).
3) х=67,4 Dх=0,28 3) х=46,7 Dх=0,33
у=4,57 Dу=0,14 у=5,47 Dу=0,15 
z=1,814 Dz=0,013. z=1,711 Dz=0,012.
4) х1=6,18174 4) х1=9,17514
x2=1,17564 x2=1,74116
х3=0,97415. х3=0,87445.
№ 7 № 8
1) 2/21=0,095;  =4,69. 1)23/15=1,53;
=4,69. 1)23/15=1,53; 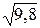 =3,13.
=3,13.
2) а) 2,4543 (±0,0032); 2) а) 23,574; d=0,2%;
б) 24,5643; d=0,1%. б) 8,3445 (±0,0022).
3) х=27,5 Dх=0,14 3) х=39,4 Dх=0,31
у=8,15 Dу=0,11 у=6,54 Dу=0,13 
z=2,817 Dz=0,009. z=2,154 Dz=0,011.
4) х1=8,12514 4) х1=7,16417
x2=1,85412 x2=1,75344
х3=0,75416. х3=0,91415.
№ 9 № 10
1)6/11=0,545; 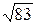 =9,11. 1)17/19=0,889;
=9,11. 1)17/19=0,889; 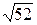 =7,21.
=7,21.
2) а) 21,68563; d=0,3% 2) а) 13,537 (±0,0026);
б) 3,7834 (±0,0041). б) 7,521; d=0,12%.
3) х=44,5 Dх=0,29 3) х=48,3 Dх=0,29
у=8,15 Dу=0,14 у=5,71 Dу=0,15 
z=1,759 Dz=0,09. z=1,684 Dz=0,011.
4) х1=8,16744 4) х1=9,17127
x2=1,81234 x2=1,94564
х3=0,81514. х3=0,81576.
№ 11 № 12
1)21/29=0,723; 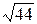 =6,63. 1)50/19=2,63;
=6,63. 1)50/19=2,63; 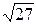 =5,19.
=5,19.
2) а) 0,3567; d=0,042% 2) а) 1,784 (±0,0063);
б) 13,6253 (±0,0021). б) 0,85637; d=0,21%.
3) х=54,7 Dх=0,28 3) х=49,4 Dх=0,24
у=6,44 Dу=0,11 у=6,71 Dу=0,12 
z=1,781 Dz=0,012. z=1,814 Dz=0,09.
4) х1=8,17564 4) х1=9,75413
x2=2,81344 x2=4,75641
х3=0,81425. х3=1,12834.
№ 13 № 14
1) 13/17=0,764; 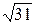 =5,56. 1)7/22=0,318;
=5,56. 1)7/22=0,318; 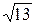 =3,60.
=3,60.
2) а) 3,6878 (±0,0013); 2) а) 27,1548 (±0,0016);
б) 15,873; d=0,42%. б) 0,3945; d=0,16%.
3) х=64,7 Dх=0,31 3) х=81,2 Dх=0,27
у=7,56 Dу=0,17 у=6,14 Dу=0,30 
z=1,749 Dz=0,09. z=1,471 Dz=0,12.
4) х1=8,94567 4) х1=8,17453
x2=6,17581 x2=0,94155
х3=1,13447. х3=6,17441.
№ 15 № 16
1) 17/11=1,545; 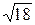 =4,243. 1)5/3=1,667;
=4,243. 1)5/3=1,667; 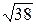 =6,16.
=6,16.
2) а) 0,8647 (±0,0013); 2) а) 3,7542; d=0,32%;
б) 24,3618; d=0,22%. б) 0,98351 (±0,00042).
3) х=74,9 Dх=0,29 3) х=84,6 Dх=0,28
у=7,15 Dу=0,22 у=6,48 Dу=0,19 
z=1,916 Dz=0,11. z=1,864 Dz=0,09.
4) х1=9,53475 4) х1=9,75481
x2=6,18445 x2=5,17841
х3=1,12417. х3=1,28412.
№ 17 № 18
1)49/13=3,77; 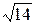 =3,74. 1)13/7=1,857;
=3,74. 1)13/7=1,857; 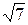 =2,64.
=2,64.
2) а) 83,736; d=0,085% 2) а) 2,8867; d=0,43%;
б) 5,6483 (±0,0017). б) 32,7486 (±0,0012).
3) х=84,7 Dх=0,31 3) х=84,7 Dх=0,28
у=5,47 Dу=0,21 у=6,47 Dу=0,15 
z=2,754 Dz=0,13. z=1,754 Dz=0,09.
4) х1=8,17564 4) х1=7,94754
x2=5,41746 x2=6,53427
х3=2,11456. х3=1,12147.
№ 19 № 20
1) 19/12=1,58; 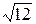 =3,46. 1)51/11=4,64;
=3,46. 1)51/11=4,64; 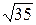 =5,91.
=5,91.
2) а) 4,88445 (±0,00052); 2) а) 38,4258 (±0,0014);
б) 0,096835; d=0,32%. б) 0,66385; d=0,34%.
3) х=16,4 Dх=0,21 3) х=45,7 Dх=0,29
у=7,15 Dу=0,16 у=7,17 Dу=0,15 
z=2,127 Dz=0,09. z=1,214 Dz=0,12.
4) х1=7,12415 4) х1=7,15427
x2=8,75112 x2=3,74184
х3=0,75927. х3=0,84415.
№ 21 № 22
1) 18/7=2,57;  =4,69. 1)17/9=2,11;
=4,69. 1)17/9=2,11;  =4,12.
=4,12.
2) а) 0,39642 (±0,00022); 2) а) 5,8425; d=0,23%;
б) 46,453; d=0,15%. б) 0,66385 (±0,00042).
3) х=83,7 Dх=0,31 3) х=87,5 Dх=0,30
у=6,54 Dу=0,21 у=11,54 Dу=0,15 
z=1,182 Dz=0,11. z=1,768 Dz=0,09.
4) х1=8,56423 4) х1=8,76465
x2=6,75447 x2=6,74275
х3=0,98476. х3=0,95443.
№ 23 № 24
1)16/7=2,28; 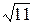 =3,32. 1)21/13=1,54;
=3,32. 1)21/13=1,54;  =7,94.
=7,94.
2) а) 24,3872; d=0,34% 2) а) 2,3684 (±0,0017);
б) 0,75244 (±0,00013). б) 45,7832; d=0,18%.
3) х=64,5 Dх=0,29 3) х=79,9 Dх=0,29
у=11,71 Dу=0,17 у=9,75 Dу=0,17 
z=1,841 Dz=0,08. z=1,165 Dz=0,09.
4) х1=9,17156 4) х1=8,17644
x2=0,75441 x2=0,19561
х3=7,14556. х3=9,17441.
№ 25 № 26
1)12/7=1,71; 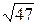 =6,86. 1)6/7=0,857;
=6,86. 1)6/7=0,857; 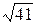 =6,40.
=6,40.
2) а) 72,354; d=0,24% 2) а) 0,36127 (±0,00034);
б) 0,38725 (±0,00112). б) 46,7843; d=0,32%.
3) х=84,5 Dх=0,32 3) х=75,9 Dх=0,34
у=8,94 Dу=0,21 у=6,12 Dу=0,17 
z=1,754 Dz=0,08. z=0,975 Dz=0,07.
4) х1=7,18171 4) х1=8,15141
x2=2,24157 x2=3,27154
х3=0,75416. х3=0,84114.
№ 27 № 28
1)23/9=2,56; 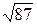 =9,33. 1)27/31=0,872;
=9,33. 1)27/31=0,872; 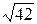 =6,48.
=6,48.
2) а) 23,7564; d=0,44% 2) а) 15,8372 (±0,0026);
б) 4,57633 (±0,00042). б) 0,088748; d=0,56%.
3) х=91,7 Dх=0,39 3) х=92,9 Dх=0,42
у=8,14 Dу=0,18 у=11,44 Dу=0,21 
z=1,124 Dz=0,06. z=1,711 Dz=0,08.
4) х1=9,97115 4) х1=8,25661
x2=2,84114 x2=3,70415
х3=0,79405. х3=1,81615.
№ 29 № 30
1)7/3=2,33; 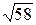 =7,61. 1)14/17=0,823;
=7,61. 1)14/17=0,823; 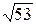 =7,28.
=7,28.
2) а) 3,87683; d=0,33% 2) а) 0,66835 (±0,00115);
б) 13,5726 (±0,0072). б) 23,3748; d=0,27%.
3) х=54,2 Dх=0,23 3) х=79,9 Dх=0,37
у=12,11 Dу=0,17 у=24,15 Dу=0,19 
z=2,124 Dz=0,10. z=1,184 Dz=0,12.
4) х1=7,12415 4) х1=9,87154
x2=4,90415 x2=3,91164
х3=0,12715. х3=1,17156
Функции к вариантам третьих заданий
№ 1-2 u = x×y2×z3
№ 3-4 u = x3×y2×z
№ 5-6 u = x×y3×z2
№ 7-8 u = x2×y×z3
№ 9-10 u = x3×y2×z
№ 11-12 u = x3×y×z2
№ 13-14 u = x2×y3×z
№ 15-16 u = x2×y2×z3
№ 17-18 u = x2×y2×z2
№ 19-20 u = x3×y2×z2
№ 21-22 u = x2×y3×z2
№ 23-24 u = x2×y3×z3
№ 25-26 u = x×y4×z2
№ 27-28 u = x4×y×z
№ 29-30 u = x×y4×z
3.4. Порядок выполнения заданий
1. Определить: какое из двух равенств точнее.
За точные числа взять значения данных выражений с большим числом десятичных знаков (на три). После определения погрешности каждого выражения, написать вывод с его обоснованием.
2. Найти интервалы точного числа двумя способами:
а) через абсолютную погрешность;
б) через относительную погрешность.
Округлить числа, оставив только верные знаки. Определить предельную абсолютную и предельную относительную погрешности полученных приближенных чисел.
3. Вычислить значение функции u и предельную абсолютную и относительную ошибки функции u для данных значений х, у, z и абсолютных погрешностей аргументов. Значение 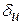 найти двумя способами:
найти двумя способами:
а) по формуле относительной погрешности непрерывной дифференцируемой функции. Для этого необходимо вначале получить формулу относительной погрешности для предложенной функции, исходя из оценки погрешности непрерывной дифференцируемой функции в общем виде (3.8);
б) по определению относительной погрешности,
г) сравнить относительные погрешности, найденные разными способами и по результатам сравнения написать вывод.
4. Найти допустимые абсолютные погрешности аргументов, которые позволяют вычислить значение данной функции u = х1×х2 + х2×х3 + х1×х3 с четырьмя верными знаками после запятой.
Для этого предварительно вывести формулы абсолютных погрешностей аргументов заданной функции, исходя из решения обратной задачи теории погрешностей в общем виде (3.9).
3.5. Решение одного варианта
1) 9/11=0,818; 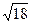 =4,24;
=4,24;
2) а) 72,353(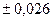 ); б) 2,3544;
); б) 2,3544; 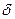 =0,2%;
=0,2%;
3) а) 0,4357; б) 12,384.
1) Находим значения данных выражений с большим числом десятичных знаков: 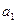 =9/11=0,81818…,
=9/11=0,81818…, 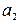 =
= 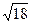 =4,2426. Затем вычисляем предельные абсолютные погрешности:
=4,2426. Затем вычисляем предельные абсолютные погрешности:
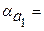
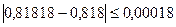 ,
,  =
= 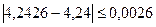 .
.
Предельные относительные погрешности составляют
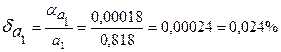 ,
,
 .
.
Вывод. Так как 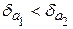 , то равенство 9/11=0,818 является более точным.
, то равенство 9/11=0,818 является более точным.
2) а) Пусть 72,353(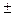 0,026). Согласно условию, предельная абсолютная
0,026). Согласно условию, предельная абсолютная  погрешность
погрешность 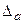 =0,026, значит, число верных знаков m=3, а =72.4 (т.е. в числе 72,353 верными являются цифры 7, 2, 3). Предельная абсолютная погрешность полученного приближения
=0,026, значит, число верных знаков m=3, а =72.4 (т.е. в числе 72,353 верными являются цифры 7, 2, 3). Предельная абсолютная погрешность полученного приближения 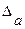 =0,026+0,047=0,073. Предельная относительная погрешность приближения а
=0,026+0,047=0,073. Предельная относительная погрешность приближения а 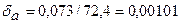 . Интервалы точного числа через предельную абсолютную погрешность (3.3):
. Интервалы точного числа через предельную абсолютную погрешность (3.3):
72,4-0,073 £ А £ 72,4+0,073
72,327£ А £ 72,473,
через предельную относительную погрешность (3.4):
72,4(1-0,00101) £ А £ 72,4(1+0,00101)
72,327£ А £ 72,473.
Вывод. В обоих случаях получили один и тот же интервал. Это говорит о правильности расчётов.
б) а =2,3544; 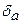 =0,2%=0,002;
=0,2%=0,002; 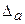 =
= 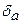 × а= 0,00471.
× а= 0,00471.
Далее аналогично вычислениям в предыдущем пункте.
3) а) u=x×y2×z3, х = 1,2; у = 2,1; z = 1,6; Dх = 0,17; Dу = 0,05; Dz=0,02.
u (1,2; 2,1; 0,6)= 21,67603.
Формула (3.7) для рассматриваемой функции имеет вид:
Du=y2×z3Dх+2×х×у×z3×Dу+3×х×у2×z2×Dz.
Для заданных значений Du=4,915814.
Исходя их формулы (3.8), получим выражение для относительной погрешности:
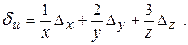
Отсюда, 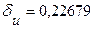 .
.
б) 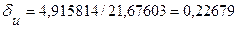 .
.
Вывод. Относительные погрешности, найденные разными способами совпадают, что подтверждает правильность полученной формулы.
4) Для функции u=x2+y2+z3 выражения допустимых абсолютных погрешностей аргументов (3.9) имеют вид:
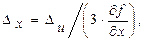
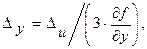
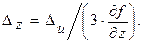
Пусть х =12,14; у =7,89; z =2,17; Du=0,00005 (по условию задачи на стр. 8). Тогда Dх=0,0000041; Dу=0,0000063; Dz=0,000023.
3.6. Вопросы для самопроверки знаний
по лабораторной работе №1
1. Что называется ошибкой или погрешностью 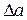 приближенного числа a?
приближенного числа a?
2. Что называется абсолютной погрешностью 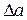 приближенного числа a?
приближенного числа a?
3. Что называется предельной абсолютной погрешностью 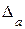 приближения a?
приближения a?
4. Что называется предельной абсолютной погрешностью 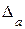 приближения a?
приближения a?
5. Что называется предельной относительной погрешностью 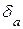 приближения
приближения 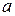 ?
?
6. Имеется ли связь между положительным приближенным числом а с n верными десятичными знаками и его относительной погрешностью 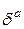 ?
?
7. Если известна предельная относительная погрешность 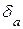 приближения
приближения 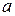 , можно ли указать интервал точного числа А?
, можно ли указать интервал точного числа А?
8. Чем могут быть обусловлены систематические погрешности?
9. Чем вызываются случайные погрешности геологических измерений?
10. Могут ли геологические данные осложнены грубыми погрешностями и чем они обусловлены?
4. ЛИНЕЙНАЯ АЛГЕБРА
4.1. Цель работы
Овладеть точными и приближёнными методами решения систем линейных алгебраических уравнений, научиться находить оценку точности найденного решения и определять пороговые значения, позволяющие остановить итерационный процесс после нахождения решения с заданной точностью.
4.2. Основные теоретические положения
Методы решения систем линейных алгебраических уравнений (СЛАУ) делятся на две группы:
1) точные методы, представляющие собой конечные алгоритмы нахождения корней системы (таковы, например, метод Гаусса, правило Крамера, метод Халецкого и др.);
2) итерационные методы, позволяющие получать корни системы с заданной точностью путем построения конечной, а чаще бесконечной последовательности приближений, итераций (к их числу относятся метод простых итераций, метод Зейделя, метод релаксаций и др.).
4.1.1. Метод простых итераций. Рассмотрим систему линейных уравнений вида
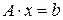 , (4.1)
, (4.1)
где 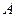 - квадратная матрица, причем
- квадратная матрица, причем  ,
, 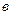 и
и 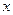 - n-мерные вектора,
- n-мерные вектора, 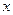 - неизвестный (искомый) вектор.
- неизвестный (искомый) вектор.
Приведем систему (4.1) к виду
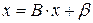 , (4.2)
, (4.2)
где 
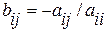 ,
, 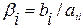 .
.
Метод простых итераций состоит в следующем. Выбирается произвольный вектор 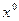 (начальное приближение) и строится итерационная последовательность векторов по формуле
(начальное приближение) и строится итерационная последовательность векторов по формуле
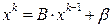 ,
, 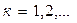 (4.3)
(4.3)
Теорема 1. Если  , то система линейных уравнений (4.2) имеет единственное решение
, то система линейных уравнений (4.2) имеет единственное решение 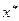 и итерации (последовательные приближения) (4.3) сходятся к решению со скоростью геометрической прогрессии.
и итерации (последовательные приближения) (4.3) сходятся к решению со скоростью геометрической прогрессии.
Через 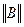 здесь обозначена норма матриц вида:
здесь обозначена норма матриц вида:
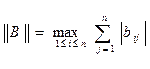 . (4.4)
. (4.4)
Для оценки точности приближения  , полученного на к -ой итерации по формуле (4.3), используется неравенство
, полученного на к -ой итерации по формуле (4.3), используется неравенство
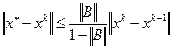 . (4.5)
. (4.5)
Через 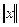 в (4.5) обозначена норма вектора вида.
в (4.5) обозначена норма вектора вида.
С точки зрения теории погрешностей левая часть (4.5) есть абсолютная погрешность приближения  СЛАУ (4.2). Неравенство (4.5) можно использовать для нахождения предельной абсолютной погрешности приближения
СЛАУ (4.2). Неравенство (4.5) можно использовать для нахождения предельной абсолютной погрешности приближения  , на основе правой части формулы (4.5).
, на основе правой части формулы (4.5).
Из формулы (4.5) можно найти величину, позволяющую останавливать итерационный процесс (4.3) в автоматическом режиме, если задана точность 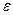 , с которой требуется найти приближенное решение. Действительно,
, с которой требуется найти приближенное решение. Действительно,  , а величина
, а величина 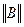 определяется по формуле (4.4). Для рассматриваемой ситуации из (4.5) получаем
определяется по формуле (4.4). Для рассматриваемой ситуации из (4.5) получаем 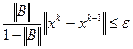 . Из этого неравенства следует
. Из этого неравенства следует
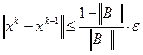 . (4.6)
. (4.6)
Неравенство (4.6) должно проверяться на каждой итерации. Как только оно будет выполнено, итерационный процесс должен быть остановлен, так как требуемая точность достигнута.
4.1.2. Метод Зейделя. Рассмотрим СЛАУ (4.2). Метод Зейделя состоит в том, что итерации производятся по формуле
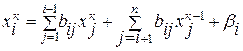 , (4.7)
, (4.7)
где 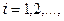
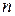 ,
, 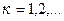
Итерации (4.7) по методу Зейделя отличаются от простых итераций (4.2) тем, что при нахождении 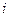 - ой компоненты
- ой компоненты 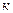 - го приближения используются уже найденные компоненты
- го приближения используются уже найденные компоненты 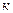 - го приближения, а именно, 1,2,…,
- го приближения, а именно, 1,2,…,  компоненты.
компоненты.
Теорема 2. Если линейная система (4.1) нормальная (симметричная и положительно определенная), то процесс Зейделя для эквивалентной ей приведенной системы (4.2) всегда сходится из любого начального вектора  .
.
Способ приведения линейной системы (4.1) к нормальному виду следует из теоремы.
Теорема 3. Если обе части линейной системы (4.1) умножить слева на транспонированную матрицу 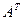 , то полученная новая система линейных уравнений
, то полученная новая система линейных уравнений 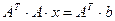 будет нормальной.
будет нормальной.
Оценка погрешности для метода Зейделя имеет вид
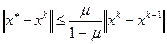 , (4.8)
, (4.8)
где 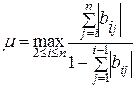 .
.
4.1.3. Метод Халецкого. Этот метод (точный) основан на том, что почти всякую квадратную матрицу 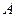 можно представить в виде произведения нижней треугольной
можно представить в виде произведения нижней треугольной 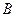 и верхней треугольной
и верхней треугольной  с единичной диагональю, т.е. в виде
с единичной диагональю, т.е. в виде 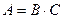 . Так как матрицы
. Так как матрицы 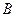 и
и  треугольные, то их элементы выражаются аналитически
треугольные, то их элементы выражаются аналитически
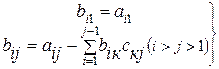 (4.9)
(4.9)
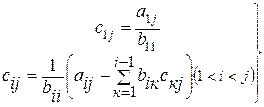 . (4.10)
. (4.10)
После нахождения матриц 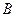 и
и  искомый вектор
искомый вектор 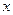 может быть вычислен из двух систем уравнений:
может быть вычислен из двух систем уравнений:
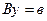 ,
, 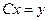 . (4.11)
. (4.11)
В силу треугольности матриц 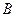 и
и  , система (4.10) решается в явном виде:
, система (4.10) решается в явном виде:
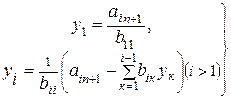 (4.12)
(4.12)
и 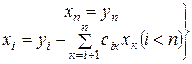 . (4.13)
. (4.13)
Этот метод получил название схемы Халецкого. В схеме применяется обычный контроль с помощью сумм. Над столбцом сумм производим те же действия, что и над столбцом свободных членов.
4.1.4. Нахождение обратной матрицы методом Халецкого. Обратной матрицей А-1 по отношению к данной А называется матрица, которая при умножении как справа, так и слева на данную матрицу А, дает единичную матрицу:
А-1×А=А×А-1=Е, (4.14)
где Е - единичная матрица.
Квадратная матрица называется неособенной, если ее определитель отличен от нуля:
det(А)¹0. … (4.15)
Теорема 4. Всякая неособенная матрица имеет единственную обратную матрицу.
Рассмотрим вычисление обратной матрицы методом Халецкого. Из равенства А=В×С следует
А-1=С-1×В-1 (4.16)
Умножая (4.16) вначале слева на С, затем справа на В, получим равенства:
А-1×В=С- 1 (4.17)
С×А-1=В-1. (4.18)
Обозначим элементы матрицы А-1 через dij, т.к. С-1 – верхняя треугольная, причем сi i=1, i =1, 2,…, n, то (4.17) представляет систему 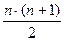 уравнений для определения d ij:
уравнений для определения d ij:
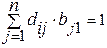 0 0…0
0 0…0
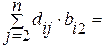 1 0…0 (4.19)
1 0…0 (4.19)
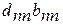 = 1
= 1
i =1, 2,…, n.
Так как В- 1 – нижняя треугольная матрица, то (4.18) представляет систему 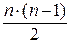 уравнений:
уравнений:
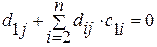 0 0…0
0 0…0
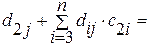 0 0…0 (4.20)
0 0…0 (4.20)
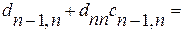 0
0
j =2, 3,…, n.
Итак, (4.19) и (4.20) является системой n2 линейных уравнений для вычисления n2 элементов А-1. Решение этой системы не содержит принципиальных трудностей. На первом шаге в каждом из уравнений (4.19) полагаем i=n и находим последовательно dnn, dn, n-1, dn1. На втором шаге из (4.20) при j=n вычисляем dn-1, n, dn-2, n,…, d1n. Затем при i=n-1 из (4.19) находим dn-1, n-1, dn-1,n-2,…, dn-1, 1 и т. д.
4.1.5. Собственные векторы и собственные значения матриц. Рассмотрим квадратную матрицу А=[aij], i,j=1, 2,…, n и n -мерный вектор х¹0.
Вектор х¹0 называется собственным вектором матрицы А, если найдется число l такое, что имеет место равенство:
А×х=l×х. (4.21)
Число l в (4.21) называется собственным значением или характеристическим числом матрицы А, соответствующим собственному вектору х.
Рассмотрим алгоритм нахождения собственных элементов нормальной (симметричной и положительно определенной) матрицы.
Если матрица нормальная, то ее собственные элементы обладают двумя важными свойствами:
1. Собственные числа l1, l2,…, ln её действительны и положительны;
2. Собственные векторы хi, i =1, 2,…, n действительны и взаимно ортогональны:
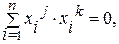 при j¹к.
при j¹к.
Исходя из теоремы существования, первый собственный вектор х1 и l1 определяются из системы линейных уравнений:
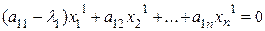
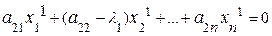
.......
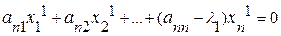
Приведем эту систему к виду, необходимому для итерационного процесса:
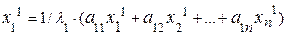
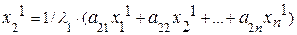
....... (4.22)
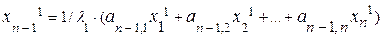
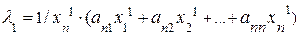 .
.
Так как координаты собственных векторов определяются с точностью до множителя пропорциональности, то одна из них произвольная, для определенности возьмем 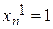 . Систему (4.21) можно решать и методом итераций, и методом Зейделя.
. Систему (4.21) можно решать и методом итераций, и методом Зейделя.
Для определения l2 и х2 СЛАУ имеет вид:
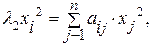 i=1, 2,…, n.
i=1, 2,…, n.
Из соотношения ортогональных векторов х1 и х2:
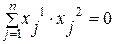
исключим одну из компонент вектора х2, например, хn2. Тогда система для определения l2 и х2 примет вид:
 i = 1, 2,…, n-2
i = 1, 2,…, n-2
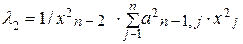 . (4.23)
. (4.23)
Полагая 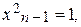 решим системы (4.23) и тем самым найдем l2 и х2.
решим системы (4.23) и тем самым найдем l2 и х2.
Варианты заданий
Дата добавления: 2015-12-20; просмотров: 17; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
