Вопрос 15) центр масс. Движение центра масс
Рассмотрим т.С, положение которой определяется радиус-вектором: 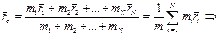
центр масс, m – масса системы.
Декартовы координаты центра масс равны проекциям rc на координатные оси: 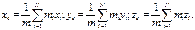
Таким образом, центр масс движется так, как двигалась бы МТ с массой, равной массе системы под действием результирующей всех внешних сил, приложенных к телам системы. Замкнутая система Þас = 0, т.е. центр масс такой системы движется прямолинейно и равномерно либо покоится.
Система отсчета, относительно которой центр масс покоится – система центра масс (ц-система). Данная система – инерциальная. 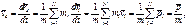
Закон сохранения импульса 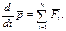
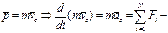 уравнение движения центра масс.
уравнение движения центра масс.
Вопрос 16) Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
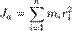 , где: mi — масса i-й точки, ri — расстояние от i-й точки до оси.
, где: mi — масса i-й точки, ri — расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
|
|
|
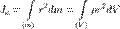 ,где:
,где:  — масса малого элемента объёма тела
— масса малого элемента объёма тела 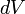 ,
, 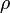 — плотность,
— плотность,
 — расстояние от элемента
— расстояние от элемента 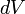 до оси a.
до оси a.
Если тело однородно, то есть его плотность всюду одинакова, то 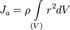
| Описание | Положение оси a | Момент инерции Ja |
| Материальная точка массы m | На расстоянии r от точки, неподвижная | 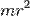
|
| Полый тонкостенный цилиндр или кольцо радиуса r и массы m | Ось цилиндра | 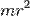
|
| Сплошной цилиндр или диск радиуса r и массы m | Ось цилиндра | 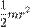
|
| Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1 | Ось цилиндра | 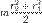
|
| Сплошной цилиндр длины l, радиуса r и массы m | Ось перпендикулярна к цилиндру и проходит через его центр масс | 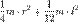
|
| Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m | Ось перпендикулярна к цилиндру и проходит через его центр масс | 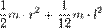
|
| Прямой тонкий стержень длины l и массы m | Ось перпендикулярна к стержню и проходит через его центр масс | 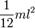
|
| Прямой тонкий стержень длины l и массы m | Ось перпендикулярна к стержню и проходит через его конец | 
|
| Тонкостенная сфера радиуса r и массы m | Ось проходит через центр сферы | 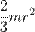
|
| Шар радиуса r и массы m | Ось проходит через центр шара | 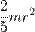
|
| Конус радиуса r и массы m | Ось конуса | 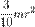
|
| Равнобедренный треугольник с высотой h, основанием a и массойm | Ось перпендикулярна плоскости треугольника и проходит через вершину | 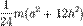
|
| Правильный треугольник со стороной a и массой m | Ось перпендикулярна плоскости треугольника и проходит через центр масс | 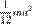
|
| Квадрат со стороной a и массой m | Ось перпендикулярна плоскости квадрата и проходит через центр масс | 
|
|
|
|
Вопрос 17) Вычислить момент инерции однородного диска толщиной. З а элементарную массу бесконечно тонкого цилиндра радиусом r, толщиной dr и высотой д примем 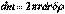 .
.
Тогда момент инерции диска 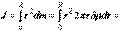
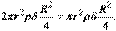
Учитывая, что масса всего диска 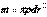 ,
,
получим 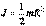 .
.
Итак, момент инерции – это аналог массы и является мерой инерции вращающегося тела. Однако масса тела не зависит от характера движения, а значение момента инерции зависит от того, относительно какой оси он вычисляется. Если известен момент инерции тела относительно какой-либо оси. О, то момент инерции относительно параллельной оси, отстоящей от первой на расстоянии R, можно вычислить, используя теорему Штейнера: 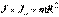 .
.
Вопрос 18) Теорема Гюйгенса — Штейнера, или просто теорема Штейнера (названа по имени швейцарского математика Якоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса): момент инерции тела 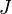 относительно произвольной оси равен сумме момента инерции этого тела
относительно произвольной оси равен сумме момента инерции этого тела 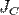 относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела
относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела  на квадрат расстояния
на квадрат расстояния 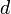 между осями:
между осями: 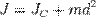 где:
где:
|
|
|
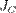 — известный момент инерции относительно оси, проходящей через центр масс тела,
— известный момент инерции относительно оси, проходящей через центр масс тела,
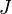 — искомый момент инерции относительно параллельной оси,
— искомый момент инерции относительно параллельной оси,
 — масса тела,
— масса тела,
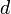 — расстояние между указанными осями.
— расстояние между указанными осями.
Вывод: Момент инерции, по определению: 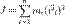
Радиус-вектор 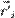 можно расписать как разность двух векторов:
можно расписать как разность двух векторов: 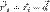 ,
,
где 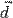 — радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид:
— радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид: 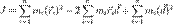
Вынося за сумму 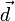 , получим:
, получим: 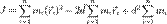
Поскольку старая ось проходит через центр масс, то суммарный импульс тела будет равен нулю: 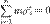
Тогда: 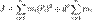
Откуда и следует искомая формула: 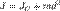 ,
,
где 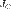 — известный момент инерции относительно оси, проходящей через центр масс тела.
— известный момент инерции относительно оси, проходящей через центр масс тела.
Дата добавления: 2015-12-18; просмотров: 17; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
