Изоморфизм. Плоские графы и теорема Эйлера.
Два графа называются изоморфными, если у них поровну вершин, и вершины каждого графа можно занумеровать числами от 1 до n, так, чтобы вершины первого графа были соединены ребром тогда и только тогда, когда соединены ребром соответствующие вершины второго графа.
Докажем, что графы изображенные на рисунке 11 изоморфны.
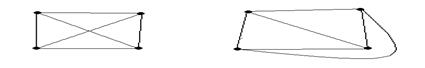
рис.11
Пронумеруем вершины первого и второго графов от 1и до 4.(рис.12)
рис.12
В первом графе соединены вершины 1 и 2, 2 и 3, 3 и 4, 1 и 4, 1 и 3, 2 и 4; заметим, что во втором графе также соединены вершины 1 и 2, 2 и 3, 3 и 4, 1 и 4, 1 и 3, 2 и 4, следовательно, данные графы изоморфны.
Для того, чтобы выяснить, изоморфны ли два графа, нужно убедиться в том, что у них:
одинаковое количество вершин
если вершины одного графа соединены ребром, то и соответствующие им вершины другого графа тоже соединены ребром. Граф, который можно нарисовать так, чтобы его рёбра не пересекались нигде, кроме вершин, называются плоским или планарным.
ТЕОРЕМА Эйлера. Для правильно нарисованного связного плоского графа имеет равенство: V-E+F=2, где V – число вершин, E - число рёбер, F – число кусков. (равенство V-E+F=2 обычно называют формулой Эйлера)
Доказательство:
Будем удалять рёбра графа до тех пор, пока не получим дерево. Посмотрим, как при удалении очередного ребра изменяются величины V, E и F. Ясно, что число вершин не изменяется, а количество рёбер уменьшается на один. Число кусков также уменьшается на один, так как при удалении ребра два примыкающих к нему куска сливаются в один. Поэтому V-E+F при такой операции не изменяется. Так как для полученного дерева V-E=1 и F=1, то V-E+F=2 и, следовательно, для исходного графа также выполняется это равенство. Значит, теорема доказана.
|
|
|
Граф, каждая вершина которого соединена с ребром любой другой вершины, называется полным.
ТЕОРЕМА Понтрягина – Куратовского: Граф является плоским тогда и только тогда, когда он не содержит (в топологическом смысле) графа с шестью вершинами типа «домики-колодцы» и полного графа с пятью вершинами. (В основном используется старинных задач о домах и колодцах, суть которой сводится к выяснению вопроса — является ли рассматриваемый граф плоским или нет, рис.13)
рис.13
Дата добавления: 2016-01-06; просмотров: 18; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!