Свойства дифференциалов высших порядков

1. .
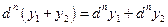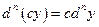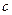2. , – постоянная.
3. .

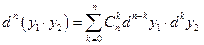Эти соотношения непосредственно следуют из соответствующих формул для производных 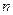-го порядка.

Далее найдем выражение для дифференциала второго порядка от сложной функции. Пусть , , 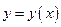имеет смысл суперпозиция 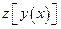и функци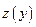и и 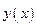дважды дифференцируемы. Тогда

.

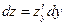Дифференцируя последнее равенство еще раз, т.е. считая запись 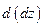, получим

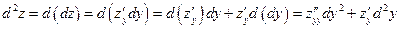. (13)

Сравнивая (10) и (13), легко увидеть их существенное различие во втором слагаемом, поскольку 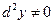. Таким образом, в отличие от дифференциалов первого порядка, дифференциалы высших порядков не обладают свойством инвариантности относительно выбора переменных.

Справедливость выражения (13) подтверждается делением обеих его частей на 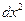, откуда следует выражение

,

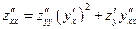совпадающая с (6).

Аналогичным образом вычисляются дифференциалы и производные высших порядков сложной функции.

 

2. Теоремы Ферма, Ролля и Лагранжа. Теорема Коши.

ТЕОРЕМА ФЕРМА. Пусть функция 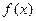определена на некотором интервале 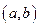и в точке 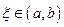принимает наиболь­шее или наименьшее значение на 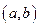. Если производная 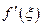суще­ствует, то она равна нулю.

Доказательство.

Пусть для определенности функция 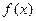в точке 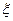принимает наибольшее значение, т.е. для всех 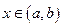. Тогда если ,

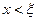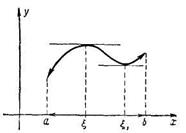
, (14)

и если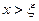

 

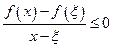. (15)

Если существует производная 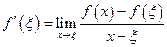, то в пределе при 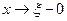из неравенства (14) получим, что 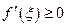, а из неравенства (15) при 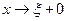, что 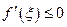, что возмож­но лишь в случае .

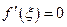Геометрическая интерпретация теоремы Ферма состоит в том, что, если в точке 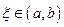функция 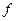принимает наибольшее или наименьшее значения, то касательная в точке 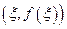к графику функции параллельна оси 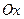(см. рис).

Замечание. Аналогичная теорема, сформулированная для отрезка 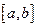оказывается несправедливой, если максимум или минимум достигаются на одном из концов этого отрезка 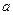или 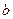. Так функция 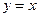на отрезке достигает минимума при 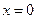и принима­ет наибольшее значение в 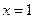. Однако ее производная в этих точках равна единице.

ТЕОРЕМА РО’ЛЛЯ. Пусть функция :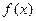

1) непрерывна на отрезке ;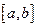

2) имеет в каждой точке интервала 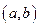производную;

3) .

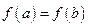Тогда существует такая точка 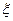, что , .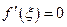

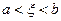Доказательство.

Как известно, функция, непре­рывная на отрезке, достигает на нем наибольшего и наименьшего значения. Пусть 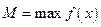, , 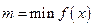тогда для всех 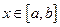выполняется неравенство .

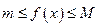Если 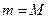, то функция 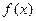постоянна и, значит, 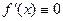на 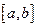. В качестве точки 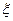можно взять любую точку интервала .

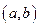Если же 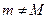то из условия 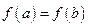следует, что хоть одно из значени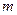й или 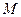не принимается на концах отрезка 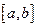. Пусть этим значением является 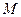, т.е. существует такая точка 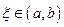, что 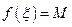. В этом случае из теоремы Ферма следу­ет, что .

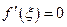Геометрически теорема Ролля означает, что у графика непре­рывной на отрезке и дифференцируемой внутри его функции, при­нимающей на концах этого отрез­ка одинаковые значения, сущест­вует точка, в которой касательная параллельна оси абсцисс.

Заметим, что все предпосылки теоремы Ролля существенны. Так, функция 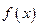, определенная на отрезке и равная 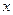, есл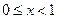и , и 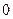, если 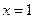, удовлетворяет условиям 2 и 3, но не удовлетворяет условию 1; функция 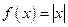, 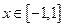; и удовлетворяет условиям 1 и 3, но не удовлетворяет условию 2; функция 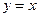, 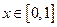удовлетворяет условиям 1 и 2, но не удовлетворяет условию 3. Для всех этих функций не существует точки, в которой их про­изводная обращалась бы в нуль.

ТЕОРЕМА ЛАГРАНЖА. Пусть функция 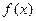непрерывна на от­резке 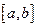и имеет производную в каждой точке интервала 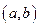, тогда существует такая точка 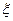, что

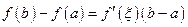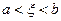, . (16)

Эта теорема является, очевидно, обобщением теоремы Ролля.

Доказательство.

Рассмотрим вспомогательную функцию

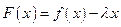, (17)

где число 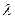выбирается из требования 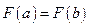. Тогда 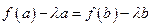, откуда

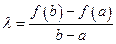. (18)

Для функции 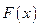выполнены все условия теоремы Ролля: 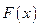непрерывна на отрезке 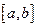, дифференцируема на интервале 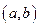и принимает на концах одинаковые значения, поэтому существует такая точка 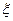, что 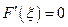, 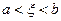. Из (17) получаем
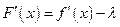, поэтому 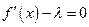. Подставляя выражение (18) для 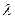, получим

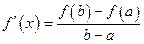, (19)

что равносильно (16).

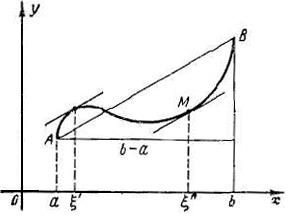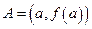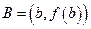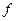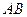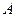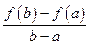Рассмотрим геометрический смысл тео­ремы Лагранжа (рис). Пусть , – ­точки графика функции , – хорда, соединяющая точки и . Тогда отношение равно тангенсу угла наклона 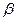хорды 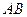к оси 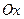, т. е.

.

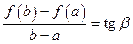Как известно, производная 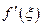, равна тангенсу уг­ла наклона 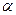касательной к графику функции 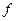в точке 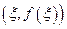, т. е.

.

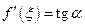Тогда равенство (19) может быть переписано в виде

.

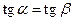Таким образом, теорема Лагранжа показывает, что в условиях теоремы должна найтись точка 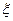, в которой касательная к графику парал­лельна хорде 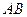. Такая точка может быть не единственной.

Приведем другие формы записи выражения (16). Пусть 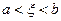и 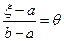. Тогда

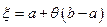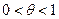, . (20)

Обратно, если 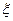выражается по формуле (20), то 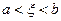. Таким образом, в виде (20) могут быть представлены все точки интервала 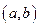и только эти точки. Поэтому формула (16) может быть записана в виде

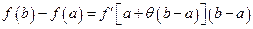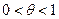, . (21)

Положим теперь , и, значит, 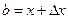, тогда (21) перепишется в виде

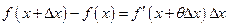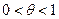, . (22)

Выражение (22) и равносильные ему выражения (21) и (16), называется формулой конечных приращений Лагранжа, или просто формулой конечных приращений в отличие от прибли­женного равенства

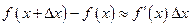, (23)

которое иногда называют формулой бесконечно малых приращений.

Смысл (23) состоит в том, что левая и правая части этого выражения для дифференцируемой в точ­ке 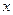функции 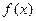равны между собой «с точностью до бесконечно малых более высокого порядка, чем приращение ».

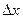Замечание. Формула Лагранжа (16) может быть переписана в виде

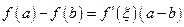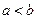, . (24)

Отсюда следует, что равенство (16) справедливо не толь­ко в случае 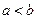, но и в случае .

С помощью теоремы Лагранжа можно доказать следующую важную лемму.

Лемма. Пусть функция :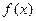

1) определена на некотором промежутке (конечном или беско­нечном);

2) имеет производную, равную нулю;

3) непрерывна в каждом из концов рассматриваемого промежут­ка, если он ему принадлежит.

Тогда функция 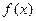постоянна на указанном промежутке.

Доказательство.

Каковы бы ни были две точк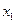и и 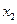, , 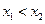рассматриваемого промежутка, функция 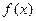удовлетво­ряет условиям теоремы Лагранжа на отрезке 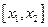. Отсюда следует

,

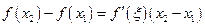где .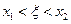

Но поскольку во всех внутренних точках промежутка производная функции равна нулю: 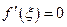, то согласно записанному выражению для любых двух точек 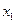и 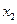из области опреде­ления функции 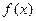выполняется равенство

,

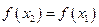то есть, функция 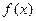постоянна.

Следствие. Пусть две функци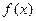и и 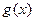дифференцируемы во всех внутренних точках некоторого промежутка и в этих точках равны их производные:

,

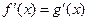а на концах промежутка (если они в него входят) функци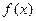и и 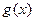непрерывны. Тогда эти функци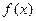и и 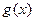отличаются на рассматриваемом про­межутке лишь на постоянную

.

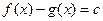Доказательство.

Введем функцию 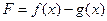. Эта функция удовлетворяет условиям леммы. В частности, 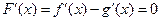во внутренних точках про­межутка. Тогда .

ТЕОРЕМА КОШИ. Пусть функци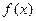и и :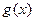

1) непрерывны на отрезке ;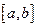

2) имеют производные в каждой точке интервала ;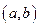

3) производная 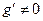во всех точках интервала .

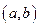Тогда существует такая точка 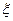, для которой

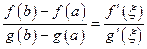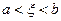, . (25)

Из условий теоремы следует, что выражение (25) имеет смысл при .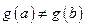

Доказательство.

Рассмотрим вспомогательную функ­цию

,

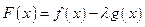где число 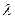выберем из условия 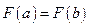, т.е. . Тогда

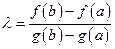. (26)

Функция 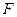удовлетворяет всем условиям теоремы Ролля, поэтому существует такая точка 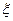, что 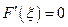, 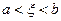. Но поскольку , получаем

.

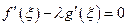Отсюда следует

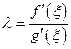. (27)

Сравнивая (26) и (27), получим выражение (25), на­зываемую формулой конечных приращений Коши.

Формула конечных приращений Лагранжа (16), (21) и (22) явля­ется частным случаем выражения (25) при .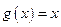

В рассмотренных теоремах Ролля, Лагранжа и Коши речь идет о существовании неко­торой точки 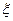(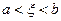), так называемой, «средней точки», для которой выполняется то или иное равенство.

 

Правила Лопиталя

Использование производных позволяет в ряде случаев упростить вычисление пределов функций. Особую важность эта особенность приобретает при раскрытии, так называемых, неопределенностей, когда в результате формальной подста­новки величины 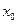, к которому стремится 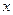, приводит к выражениям вида 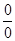, , 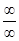, , , , 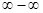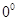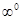или .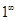

Для разрешения таких неопределенностей наряду с основным методом нахождения пределов функций и методом выделения главной части существуют специальные методы, получившие название правил Лопиталя.

Вначале рассмотрим способы разрешения неопределенностей вида .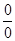

ТЕОРЕМА. Пусть функци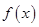и и 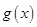, определены на полуинтервале 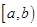и удовлетворяют условиям:

1) ;

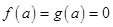2) существуют односторонние производные 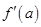и 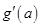, причем .

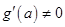Тогда

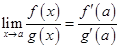. (28)

Обобщением данной теоремы является теорема, не требующая обязательного существования производных 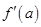и .

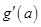ТЕОРЕМА. Пусть функци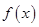и и :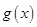

1) дифференцируемы на интервале ;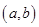

2) ;

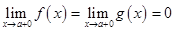3) 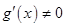для всех ;

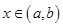4) существует (конечный или бесконечный) предел .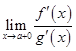

Тогда существует предел

. (29)

Рассмотренные теоремы остаются справедливыми и при случае .

ТЕОРЕМА. Пусть функци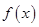и и :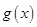

1) дифференцируемы при ;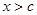

2) , ;

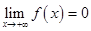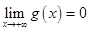3) 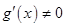(для всех 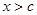) существует (конечный или бесконечный) предел

.

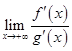Тогда существует предел

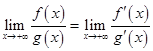. (30)

Справедливость последней теоремы сохраняется и при замене .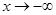

Правила раскрытия неопределенностей вида 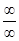аналогичны.

В качестве примера использования правила Лопиталя рассмотрим предел

, .

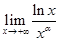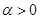Учитывая, что производные числителя и знаменателя имеют вид

, ,

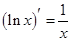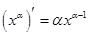в соответствии с (30) получим

.

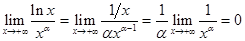Это означает, что при 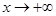функция 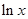растет медленнее, чем любая положительная степень .

В ряде задач требуется многократное использование правил Лопиталя. В качестве такого примера рассмотрим предел 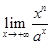, где – натуральное число и .

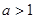Тогда, в соответствии с (30), находим

.

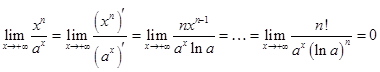Таким образом, при 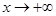любая степень 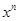растет медлен­нее, чем показательная функция , .

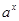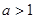При этом следует иметь в виду, что правила Лопиталя не являются универсальными. В качестве примера рассмотрим предел

.

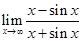Его вычисление по правилам Лопиталя дает

.

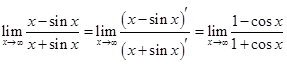При этом, поскольку предел

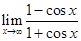
не существует, использование правил Лопиталя не приводит к требуемому результату, поскольку не выполняется условие соответствующей теоремы.

При этом, данная неопределенность вида 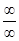может быть легко раскрыта традиционным способом:

.

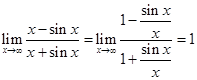Неопределенности вида 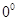, , 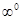или 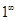раскрываются с использованием предварительного логарифмирования. В качестве примера найдем . Вначале вычислим предел

.

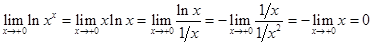Потенцируя полученное выражение и учитывая непрерывность показательной функции, находим

.

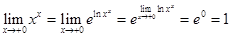Неопределенности вида 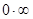и 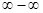следует привести к виду 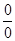или 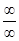. При этом, как и всегда при применении правила Лопи­таля, по ходу вычислений рекомендуется упрощать получающиеся выражения.

В качестве примера найдем предел

.

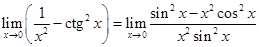Заметим, что

.

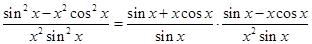Предел первого сомножителя правой части находится непо­средственно и равен

,

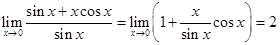а предел второго – с применением правила Лопиталя:

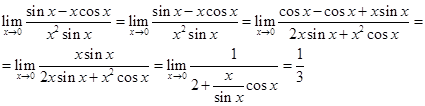
Таким образом, окончательно получаем

.

---

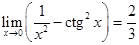Дата добавления: 2016-01-06; просмотров: 18; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!