Свойства производных высших порядков
ТЕОРЕМА. Пусть функции 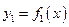 ,
, 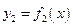 имеют производные
имеют производные 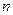 -го порядка в точке
-го порядка в точке 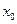 , тогда функции
, тогда функции 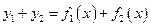 ,
, 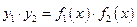 также имеют производные
также имеют производные 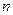 -го порядка в точке
-го порядка в точке 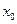 , причем
, причем
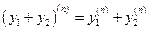 , (3)
, (3)
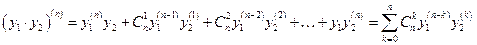 , (4)
, (4)
где 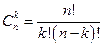 обозначает число сочетаний из
обозначает число сочетаний из 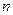 элементов по
элементов по 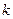 ,
, 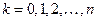 . Формула (4) называется формулой Лейбница.
. Формула (4) называется формулой Лейбница.
Следствие. Если 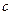 – постоянная, а
– постоянная, а 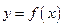 – функция, имеющая производную
– функция, имеющая производную 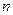 -го порядка в точке
-го порядка в точке 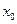 , то и функция
, то и функция 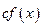 также имеет производную порядка
также имеет производную порядка 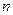 в точке
в точке 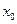 , причем
, причем
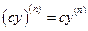 . (5)
. (5)
Далее рассмотрим производные высших порядков от сложных функций. Вначале рассмотрим производную второго порядка.
Пусть функция 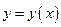 имеет вторую производную в точке
имеет вторую производную в точке 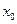 , а функция
, а функция  имеет вторую производную в точке
имеет вторую производную в точке 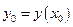 . Тогда в некоторой окрестности точки
. Тогда в некоторой окрестности точки 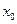 существует сложная функция
существует сложная функция 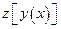 , которая также имеет в точке
, которая также имеет в точке 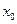 вторую производную, причем
вторую производную, причем
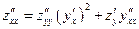 . (6)
. (6)
Покажем справедливость данного выражения. Поскольку существуют производные 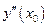 и
и 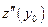 , то существуют производные
, то существуют производные 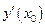 и
и 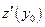 . Следовательно, функции
. Следовательно, функции 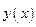 и
и 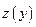 в точках
в точках 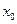 и
и 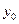 непрерывны. Поэтому в некоторой окрестности точки
непрерывны. Поэтому в некоторой окрестности точки 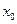 имеет смысл сложная функция
имеет смысл сложная функция 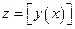 . Дифференцируя ее и опуская для простоты обозначение аргумента, имеем
. Дифференцируя ее и опуская для простоты обозначение аргумента, имеем
 .
.
Вычисляя вторую производную, получаем
 ,
,
что соответствует (6).
Аналогичным образом вычисляются производные высших порядков сложной функции. Однако в виду громоздкости соответствующие формулы мы приводить не будем.
Найдем выражение производной 2-го порядка от обратной функции. Пусть в некоторой окрестности точки 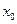 функция
функция 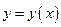 определена, непрерывна и строго монотонна и пусть в точке
определена, непрерывна и строго монотонна и пусть в точке 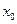 существуют производные
существуют производные 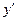 и
и 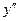 , причем
, причем 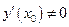 . Тогда обратная функция
. Тогда обратная функция 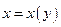 также имеет вторую производную в точке
также имеет вторую производную в точке 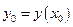 , причем она может быть выражена через производные
, причем она может быть выражена через производные 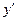 и
и 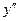 функции
функции 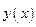 в точке
в точке 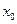 .
.
Как известно, 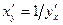 . Вычисляя произвольную по
. Вычисляя произвольную по  от обеих частей и вычисляя ее от правой части по правилу сложной функции, получим
от обеих частей и вычисляя ее от правой части по правилу сложной функции, получим
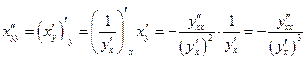 . (7)
. (7)
Аналогично при соответствующих предположениях вычисляются и производные высших порядков для обратной функции.
Далее рассмотрим функции  , заданные параметрически:
, заданные параметрически:
 ,
, 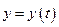 .
.
Тогда, если существуют производные 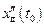 и
и 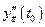 , то существует и производная
, то существует и производная 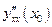 , причем
, причем
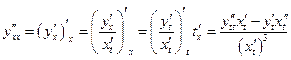 . (8)
. (8)
По аналогии с понятием производной можно рассмотреть и дифференциалы высших порядков. Будем для удобства использовать в некоторых случаях вместо символа дифференцирования 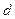 символ
символ 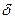 , а
, а 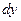 ,
, 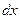 –выражения
–выражения 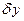 ,
, 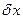 .
.
Пусть функция 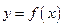 дифференцируема на некотором интервале
дифференцируема на некотором интервале 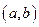 . Ее дифференциал
. Ее дифференциал
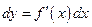
является функцией двух переменных: точки 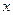 и переменной
и переменной 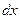 . Если функция
. Если функция 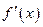 также дифференцируема в некоторой точке
также дифференцируема в некоторой точке 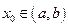 , то дифференциал от функции
, то дифференциал от функции 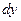 в этой точке при фиксированном
в этой точке при фиксированном 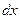 , принимает вид
, принимает вид
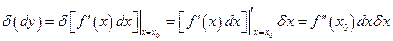 . (9)
. (9)
Опр. Значение дифференциала 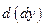 , т.е. дифференциала от первого дифференциала, называется вторым дифференциалом функции
, т.е. дифференциала от первого дифференциала, называется вторым дифференциалом функции 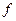 в точке
в точке 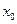 :
:
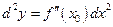 . (10)
. (10)
Аналогичным образом можно определить дифференциал 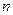 -го порядка
-го порядка 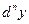 функции
функции 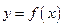 в точке
в точке 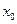 как дифференциал от дифференциала
как дифференциал от дифференциала 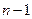 -го порядка
-го порядка 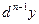 :
:
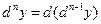 .
.
Можно показать справедливость равенства
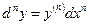 ,
, 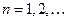 , (11)
, (11)
из которого следует еще одно выражение производной 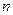 -го порядка:
-го порядка:
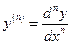 . (12)
. (12)
Дата добавления: 2016-01-06; просмотров: 21; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
