Идеальные и сферические координаты
Для решения этой задачи построим вспомогательную небесную сферу произвольного радиуса с центром в главной точке объектива О2 (рис.35).
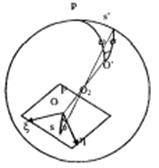
Рис. 35. Система идеальных координат на снимке
Точками р и s' на сфере обозначены северный полюс Мира и звезда (либо ИСЗ). Оптическая ось фотографической камеры пересекает сферу в точке О'. На расстоянии F (фокусное расстояние объектива) расположена плоскость снимка. Точка пересечения оптической оси с плоскостью снимка называется главной точкой снимка или оптическим центром снимка. Все точки вспомогательной небесной сферы проектируются на плоскость снимка по законам центральной проекции. В плоскости снимка можно ввести так называемую идеальную систему плоских координат. Начало этой системы совмещается с оптическим центром снимка, ось η представляет собой проекцию полукруга склонения точки О', причём направлена эта ось в сторону возрастания склонений. Ось ξ - это проекция большого круга небесной сферы, проходящего через точку О', под прямым углом к полукругу склонений. Положительное направление оси ξ совпадает с возрастанием прямых восхождений. Во введенной таким образом системе координат положение точки s на снимке определяется формулами
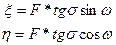 (5.5)
(5.5)
в которых σ - дута большого круга между точками О' и s' или центральный угол с вершиной в точке О2, опирающийся на эту дугу; ω – сферический угол между полукругом склонения рО' и дугой большого круга O's'. По законам центральной проекции этот угол передается без искажений и в плоскости снимка соответствует углу sOη.
|
|
|
Применяя формулы синусов, косинуса стороны и пяти элементов
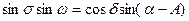 (5.6)
(5.6)
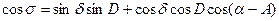 (5.7)
(5.7)
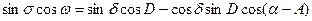 (5.8)
(5.8)
к решению сферического треугольника, отдельно показанного на рис. 36, легко выразить идеальные координаты через сферические:
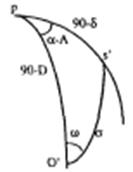
Рис. 36 Углы и стороны сферического треугольника
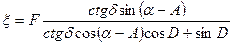 (5.9)
(5.9)
 (5.10)
(5.10)
При математической обработке снимка потребуется решать задачу, обратную к только что рассмотренной. Интересующие нас соотношения выведем, опираясь на формулы (5.9), (5.10) которые преобразуем к виду
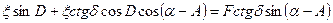 (5.11)
(5.11)
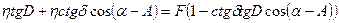 (5.12)
(5.12)
Откуда следует
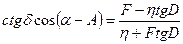 (5.13)
(5.13)
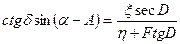 (5.14)
(5.14)
Разделив теперь последнее уравнение на предыдущее, получим выражение для прямого восхождения.
 (5.15)
(5.15)
Формула же для склонения вытекает непосредственно из (5.13):
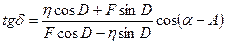 (5.16)
(5.16)
Дата добавления: 2016-01-05; просмотров: 77; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
