Модель для идеальных условий
Согласно классической модели Харриса, рассматривается непрерывное расходование запасов и мгновенное их поступление.
На рисунке 1 показан пример графика изменения запасов для такой модели.
В течение длительности цикла T идет расходование запаса, и в момент спада запасов до нуля происходит их восстановление до уровня q. Этот момент называют "точкой заказа", положение которой определяет длительность цикла.
Рисунок 1 – График изменения запасов в модели Харриса
В системах управления запасами основными вопросами являются состав и размеры издержек управления.
Рассматриваемые в модели величины, их обозначения, а также принятые относительно этих величин допущения представлены в таблице 1.
Таблица 1. Показатели систем управления запасами
| Величина | Обозначение | Единицы измерения | Допущения |
| Интенсивность спроса | a | Единицы товара в год | Спрос постоянен и непрерывен |
| Организационные издержки | S | Рублей за одну партию | Организационные издержки постоянны |
| Стоимость подлежащего переработке продукта | c | Рублей за единицу товара | Цена единицы товара постоянна |
| Издержки содержания запасов | h | Рублей за единицу товара в год | Стоимость хранения постоянна |
| Размер партии поставки | q | Единицы товара в год | Постоянная величина. |
Рассмотрим ситуации, в которых издержки, связанные с запасами, могут быть объяснены независимо друг от друга.
1. Организационные издержки – расходы, связанные с оформлением и доставкой подлежащего переработке продукта (товара), необходимые для каждого цикла складирования. Эти затраты связаны с подготовительно-заключительными операциями при поступлении сырья и подаче заявок.
2. Издержки содержания запасов – затраты, связанные с хранением и амортизацией в процессе хранения (товары могут портиться, устаревать, их количество может уменьшаться и т.п.).
3. Издержки, связанные с дефицитом, – поставка не может быть выполнена, это допускается в моделях с дефицитом, что приводит к дополнительным издержкам, обусловленным отказом.
Уравнение издержек С, связанных с запасами, сделанными в течение года, может быть записано в соответствии с таблицей 1 следующим образом:
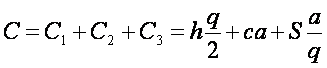, (1)
где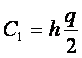 
– общие издержки содержания запасов;
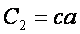– стоимость товара;
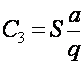– общие организационные издержки.
На рисунке 2 показан приближенный график функции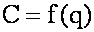 
, отвечающий формуле (1).
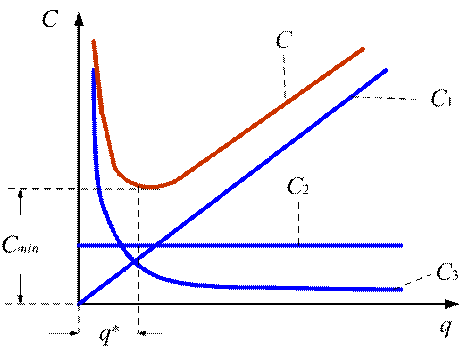
Рисунок 2 – График изменения издержек
Чтобы найти значение партии поставки, обращающее С в минимум, используем необходимое условие экстремума 
. Это действительно точка минимума, так как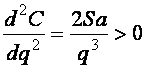 
.
Следовательно, справедливо:
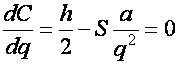. (2)
Решая последнее уравнение относительно q, найдем оптимальный размер партии поставки q *, а значит и оптимальный объем исходного материального потока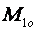 
:
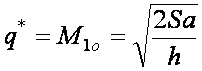. (3)
Величина q * называется оптимальным размером партии поставки товарного запаса. Уравнение (3) иногда называют формулой оптимального заказа.
Чтобы полностью удовлетворить годовой спрос a при размере поставки, равном q *, необходимо сделать a / q * поставок за год.
Таким образом, число циклов m технологической цепи в течение года можно определить как:
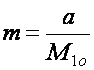, (4)
где a – годовая потребность в сырье для переработки;
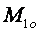– оптимальный объем исходного материального потока, вычисляемый по формуле (3).
Если подставить вместо объема исходного материального потока 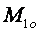в формуле (4) его выражение из (3), получим оптимальное число циклов 
:
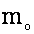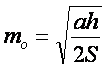. (5)
Минимальный объем финансового потока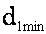 
, запускающего технологический цикл, определим по типу соотношения (1), в котором учтем, что рассматривается один цикл, а значит, и один оптимальный по объему материальный поток 
:
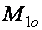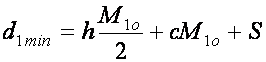. (6)
Если подставить в (4) выражение 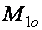из (3), получим соотношение для расчета минимального объема финансового потока 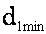, зависящее только от параметров поставок и хранения сырья:
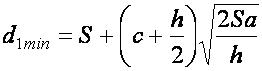. (7)
Дата добавления: 2016-01-04; просмотров: 17; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!