Газовые манометрические термометры. 1 страница

Для функции

(1.14)

которую принято называть нормальной функцией распределения, составлены таблицы для различных значений t.

Возвращаясь к рис. 1.5, найдем точки перегиба кривой и соот­ветствующие им значения –δ _k и +δ _k. Для этого приравняем вторую производную уравнения (1.13) нулю и найдем, что перегиб кривой происходит в двух точках, симметрично расположенных по обе стороны от оси ординат f (δ), при значениях ±δ _k = ±σ _n. Полученные точки перегиба разделяют область часто встречающихся случайных погрешностей от области погрешностей, редко встречающихся.

Для неограниченно большого ряда измерений 68,3% всех случайных погрешностей ряда лежит ниже данного значения σ _n и 31,7% выше его.

Параметр σ _n однозначно характеризует форму кривой распределения случайных погрешностей. Ордината f (δ) кривой распределения, соответствующая δ = 0, обратно пропорциональна σ _n; при увеличении σ _n ордината f (0) уменьшается (рис. 1.6). Так как площадь под кривой распределения всегда равна единице, то при увеличении σ _n кривая распределения 3 (рис. 1.6) становится более плоской, чем кривая 2, растягиваясь вдоль оси абсцисс. С другой стороны, при уменьшении σ _n кривая распределения 1 вытягивается вверх, одновременно сжимаясь вдоль оси абсцисс. Таким образом, малому значению σ _n соответствует преобладание малых случайных погрешностей, а вместе с тем и большая точность измерения данной величины; при большом же σ _n большие случайные погрешности встречаются значительно чаще, следова­тельно, точность измерения меньше.

Конечная цель анализа выполненных измерений состоит в определении погрешности результата наблюдения ряда значений измеряемой величины х ₁, x ₂,..., х_n и погрешности их среднего арифметического значения, принимаемого как окончательный результат измерения, относительной частоты погрешно­стей и вероятности.

Оценка точности результата наблюдения. Для оценки точности результата наблюдения служит среднее квадратическое отклонение результата наблюдения σ _n (квадрат этой величины, т.е. называется рассеянием или дисперсией результата наблюдения и обозначается обычно символом D). В реальных условиях мы имеем дело с конечными рядами наблюдаемых значений измеряемой величины, так что, определяя σ при ограниченном числе наблюдений, можем найти только приближенное значение или оценку этого отклонения, определяемого по формуле

(1.15)

где n – число наблюдений; x_i – значение величины, полученное при i -м наблюдении; – среднее арифметическое значение (результат измерений).

Выражение (1.15) при ограниченном числе наблюдений дает несмещенную оценку среднего квадратического отклонения результата наблюдений.

Для получения полного представления о точности и надежности оценки случайного отклонения результата наблюдения должны быть указаны доверительные границы, доверительный интервал и довери­тельная вероятность. При известном σ доверительные границы указываются следующим образом: нижняя граница – σ или – σ, верхняя граница + σ или + σ (сокращенно ±σ или ± σ), за пределы которых с вероятностью Р = 0,683 (или 68,3%) не выйдут значения случайных отклонений x_i – X или результатов отдельных наблюдений x_i ряда измерений. Доверительный интервал выражается в виде

I_P = ( – σ; + σ).

В зависимости от целей измерения могут задаваться и другие доверительные границы: – t_P σ или – t_P σ и + t_P σ или + t_P σ. Значения t_P для наиболее употребительных доверительных вероятностей при приведены в табл. 1.1. В инженерной практике предпочтение отдается вероятности 0,95 и 0,997.

Таблица 1.1.

Значения t_P для наиболее употребительных вероятностей при

P	0,683	0,90	0,95	0,98	0,99	0,9973
tP		1,645	1,96	2,33	2,58	3.000

 

Оценка точности результата измерения. Для оценки достоверности результата измерения, принимаемого равным среднему значению , применяют показатель точности, аналогичный показателю точности результата наблюдения. При этом согласно теории погрешностей оценка среднего квадратического отклонения результата измерения в раз меньше оценки среднего квадратического отклонения результата наблюдения (1.15). Таким образом, при числе измерений n оценка среднего квадратического отклонения результата измерения

 

(1.16)

 

Доверительные границы погрешности результата измерения ука­зываются следующим образом: нижняя граница или верхняя граница или за пределы которых с вероятностью 0,683 не выйдут погрешности результата измерения или среднее арифметическое значение . Доверительный интервал представляют в виде

В зависимости от назначения измерений может быть задана и другая доверительная вероятность. В этом случае доверительные границы записываются как или и или , а доверительный интервал

Оценка точности результата измерения при малом числе наблюдений. На практике, как правило, число измерений конечно и в боль­шинстве случаев не превышает 15 – 20 отдельных наблюдений, а при ответственных измерениях – нескольких десятков. При малом числе наблюдений () и условии, что распределение погрешностей отдельных измерений следует нормальному, пользуются для определения t_P таблицей, основанной на распределении Стьюдента.

Измерения при малом числе наблюдений чаще дают преуменьшенное значение средней квадратической погрешности по сравнению с погрешностью для достаточно большего ряда тех же измерений. Распределение Стьюдента, упрощенно говоря, учитывает это обстоятельство, и при одинаковой доверительной вероятности значение t = v/ σ больше в распределении Стьюдента, чем в нормальном. Иными словами, вероятность появления, например, одинаково боль­ших погрешностей в распределении Стьюдента, т.е. при малом числе измерений, – больше.

В табл. 1.2 приведены вычисленные по распределению Стьюдента, вероятности (1 – Р) появления погрешностей, превышающих в зависимости от числа измерений n.

Если задана вероятность, то, пользуясь выражением для Р, можно найти положительное число t_P, которое будет зависеть только от P и n.

Таблица 1.2

Вероятности (1 – Р) появления погрешностей, превышающих
, и

 

Число измерений n				Число измерений n
	0,500	0,295	0,205		0,339	0,071	0,012
	0,423	0,184	0,095		0,334	0,064	0,010
	0,374	0,116	0,030		0,331	0,062	0,008
	0,356	0,002	0,024		0,330	0,050	0,007
	0,343	0,077	0,015	∞	0,317	0,016	0,003

 

Полагая

ε = t_P , (1.17)

получаем

P ( – ε < X < + ε) = P; (1.18)

 

при этом ε будет зависеть от n, Р и значений x ₁, х ₂, х ₃,..., х_n, кото­рые входят в ε через . Выражение (1.18) позволяет достаточно точно произвести оценку приближенного равенства

При практическом применении распределения Стьюдента по­грешность ε среднего арифметического значения (результата изме­рения) при малом числе наблюдений () и заданной доверитель­ной вероятности Р определяется из значений σ или , вычисленных по формулам (1.15) или (1.16), с помощью выражения

(1.19)

Значения t_P для наиболее употребительных доверительных вероятностей Р и различных п – 1 приводятся в справочных таблицах.

При (n > 200) распределение Стьюдента сходится с нормальным.

Для оценки среднего арифметического значения , принимае­мого как окончательный результат измерения, указываются дове­рительные границы и доверительный интервал при выбранной дове­рительной вероятности. Доверительные границы указываются сле­дующим образом: нижняя граница – ε, верхняя граница + ε или сокращенно ± ε. Доверительный интервал выражается в виде

I_P = ( – ε; + ε),

где ε определяется формулой (1.19) и выражается в единицах измеряемой величины.

Если ε выражается в долях среднего арифметического значения измеряемой величины, то доверительные границы указываются следующим образом:

Оценка точности косвенных измерений. В косвенных измерениях определение значения искомой величины y производится на основании прямых измерений других величин, связанных с y функциональной зависимостью

(1.20)

где – средние арифметические значения прямых измерений с одинаковым числом отдельных наблюдений

При определении искомой величины y полагаем, что результаты измерения величин свободны от систематических погрешностей.

Погрешность результата косвенного измерения величины y зависит от погрешности результатов прямых измерений независимых друг от друга величин .

Для оценки точности результата косвенного измерения величины y применяют среднее квадратическое отклонение, вычисляемое по формуле

(1.21)

где σ₁, σ₂,...,σ _m – средние квадратические отклонения результатов измерения величин

В зависимости от требований к измерениям может быть задана различная доверительная вероятность. Обозначая для выбранной доверительной вероятности Р через ε_ν погрешности величин , связанные с σ_{ν i} или σ_ν равенством

и подставляя ε_ν в формулу 1.21, получаем

(1.22)

Погрешности σ_ν и ε_ν в формулах (1.21) и (1.22) выражаются в тех же единицах, что и искомая величина y. Если непосредственно измеряемые величины являются по своей природе разнородными, то пользуются относительными погрешно­стями этих величин.

При использовании оценок средних квадратических отклонений σ_{ν i} значение погрешности результата косвенного измерения также будет приближенно.

Приведенные выше формулы для определения погрешности результата косвенного измерения у могут быть использованы и в том случае, если у находится по отдельным значениям прямых изме­рений, т.е.

у = f (х ₁, x ₂,..., х_m).

В этом случае должно быть известно значение среднего квадра-тического отклонения

Вопрос 3

Статические характеристики измерительных устройств

В общем случае состояние (режим работы) измерительного устройства, при котором значения входного X и выходного Y сигналов не изменяются, называют статическими (стационарными или равновесными).

Статической характеристикой измерительного устройства называют функциональную зависимость выходного сигнала от входного в статическом режиме работы указанного устройства. Более точно статическую характеристику можно определить как зависимость информативного параметра выходного сигнала от информативного параметра его входного сигнала в статическом режиме. Статическая характеристика описывается в общем случае некоторым нелинейным уравнением (уравнением преобразования):

Y = f (X). (1.23)

Для измерительных преобразователей, а также измерительных приборов с неименованной шкалой или со шкалой, отградуирован­ной в единицах, отличных от единиц измеряемой величины, стати­ческую характеристику принято называть функцией преобразова­ния. Для измерительных приборов иногда статическую характери­стику называют характеристикой шкалы.

Определение статической характеристики связано с выполнени­ем градуировки, поэтому для всех средств измерений используют понятие градуировочной характеристики, под которым понимают зависимость между значениями величин на выходе и входе средства измерений, составленную в виде таблицы, графика или формулы.

На рис. 1.8 показаны виды статических характеристик измери­тельных устройств. За исключением специальных случаев, основ­ное требование, предъявляемое к статической характеристике из­мерительных устройств, сводится к получению линейной зависимо­сти между выходной и входной величинами. На практике это требование реализуется в общем случае только с некоторой при­нятой заранее погрешностью.

Кроме статической характеристики для определения метрологи­ческих свойств измерительных устройств используется ряд пара­метров.

В общем случае линейная или линеаризованная статическая характеристика средства измерения описывается уравнением вида

Y = a + kX, (1.24)

где а – постоянная, имеющая размерность Y; k – коэффициент имеющий размерность Y/X.

Если линейная статическая характеристика средства измерения проходит через начало координат (рис. 1.8, а), то уравнение 1.24 принимает вид:

Y = kX. (1.25)

Входящий в уравнения (1.24) и (1.25) коэффициент k называют коэффициентом передачи. Понятие коэффициента передачи распространяется на отдельные элементы, обладающие свойством направ­ленной передачи воздействий, и на средства измерения в целом. Однако такие средства измерений, как измерительные приборы, характеризуют не коэффициентом передачи, а чувствительностью S. В общем случае уравнение шкалы измерительного прибора с линейной связью между входной величиной и показаниями имеет вид:

y = y _н + S (x – x _н),

 

где y _н и x _н – начальные значения соответственно выходной и вход­ной величин.

Чувствительность прибора определяется по формуле

(1.26)

где y _д = у _к – у _н – диапазон изменения выходного сигнала; х _д = х _к – х _н – диапазон изменения входного сигнала.

Для средств измерений в большинстве случаев предпочтительна линейная статическая характеристика. Нелинейные статические характеристики средств измерений допускаются только в том случае, если они обусловлены применяемым принципом измерения и нелинейность не может быть полностью устранена. Мерой отклонения нелинейной характеристики от линейной служит относительная нелинейность статической характеристики, определяемая отношением Δ у / Х_N, где Δ у – максимальный отрезок выходной координаты между статической характеристикой и прямой, соединяющей начало (х _н) и конец (х _к) нелинейной характеристики (рис. 1.8, в), а Х_N – нормирующее значение (см. выше).

Под чувствительностью измерительного прибора с нелинейной статической характеристикой понимают предел отношения прираще­ния выходного сигнала Δ у к приращению входной величины Δ x:

(1.27)

Очевидно, что в случае линейной статической характеристики (см. рис. 1.8, а) чувствительность остается постоянной для любой точки шкалы. Если статическая характеристика задана в виде урав­нения у = f (х), то для определения чувствительности необходимо продифференцировать это уравнение по х. При нелинейной зависи­мости у от х чувствительность зависит от значения входного сиг­нала.

Если относительная нелинейность статической характеристики невелика или диапазон изменения х ограничен, то можно линеари­зовать характеристику, т.е. заменить реальную нелинейную зави­симость у от х приближенной линейной. Линеаризацию заданной графически характеристики осуществляют методом касательной или секущей. При линеаризации касательной (рис. 1.8, в) коэффициент передачи (или чувствительность) определяют тангенсом угла на­клона касательной в данной точке:

(1.28)

где п_х, п_у – масштабы графика у = f (х).

Линеаризация секущей позволяет, например, определить сред­нее значение коэффициента передачи (чувствительности), равное тангенсу угла наклона прямой, соединяющей начальную и конеч­ную точки характеристики (cм. рис. 1.8, в):

(1.29)

Динамические характеристики измерительных устройств

Режим работы измерительного устройства, при котором значения выходного и входного сигналов изменяются во времени, называют динамическим (нестационарным или неравновесным).

Практически все измерительные устройства имеют в своем со­ставе инерционные элементы, а именно: подвижные механические узлы, электрические или пневматические емкости, индуктивности, элементы, обладающие тепловой инерцией и т.п. Наличие инерци­онных элементов определяет инерционность всего измерительного устройства, т.е. приводит к тому, что в динамическом режиме мгно­венное значение выходного сигнала измерительного устройства за­висит не только от мгновенного значения входного сигнала, но и от любых изменений этого сигнала, т.е. от его первой и второй производных и производных более высокого порядка.

Указанные инерционные свойства измерительных устройств определяют динамической характеристикой.

Динамическая характеристика измерительного устройства в об­щем случае это зависимость между информативными параметрами выходного и входного сигналов и временем или зависимость выходного сигнала от входного в динамическом режиме.

Динамическую характеристику измерительного устройства принято описывать дифференциальным уравнением, передаточной или комплексной частотной функциями.

В подавляющем большинстве случаев динамическая характеристика измерительных устройств в линейной части статической характеристики (для измерительных устройств с линейной статической характеристикой во всем диапазоне преобразований) может быть описана дифференциальным уравнением вида

(1.30)

или соответствующей передаточной функцией

(1.31)

либо

Y(p) = W(p)X(p), (1.32)

где Y (τ) и X (τ) – выходной и входной сигналы измерительного устройства как функции времени; n – число, определяющее порядок производной.

Передаточную функцию W(p) (см. 1.32) можно рассматривать как коэффициент преобразования измерительного устройства в динамическом режиме.

Передаточная функция, как и дифференциальное уравнение, является исчерпывающей характеристикой инерционных свойств измерительного устройства. Она позволяет определить реакцию измерительного устройства на входные сигналы, изменяющиеся во времени по любому закону.

Передаточную функцию измерительных устройств удобно использовать при анализе работы последних в автоматических системах регулирования. Ее определяют обычно через переходную или временную характеристику, которая определяется как изменение во времени выходного сигнала h (τ) измерительного устройства при подаче на его вход скачкообразного сигнала, равного по значению единице входной величины.

Если высота скачкообразного входного сигнала не равна единице, а имеет некоторое значение Х_А, то по переходной характери­стике можно определить выходной сигнал, используя выражение

Y (τ) = h (τ) Х_А. (1.33)

Для определения инерционных свойств измерительных устройств по переходным характеристикам обычно используют заимствованное из теории автоматического регулирования понятие динамического звена. Переходные характеристики и передаточные функции типовых динамических звеньев известны, что позволяет по форме переходной характеристики измерительного устройства отожествить его с каким-либо типовым динамическим звеном, а следовательно, определить форму передаточной функции испытываемого измерительного устройства. Описанную процедуру принято называть идентификацией.

На рис. 1.9 показаны наиболее типичные для измерительных устройств формы переходных характеристик, т.е. кривые переходных процессов, или кривые разгона.

Для их получения в нулевой (для простоты) момент времени входной сигнал измерительного устройства скачком изменяется на Х_А от некоторого значения Х ₁ до Х ₂ (рис. 1.9, а). По окончании переходного процесса выходной сигнал измерительного устройства изменяется на Y_A от значения Y ₁ до Y ₂.

Для определения коэффициента преобразования К измеритель­ного устройства достаточно вычислить отношение Y_A/X_A.

Переходные процессы, показанные на рис. 1.9, б, в, г, соответствуют типовым усилительному (безынерционному), апериодическому первого порядка и колебательному звеньям.

Процесс, представленный на рис. 1.9, б, характерен для электронных измерительных устройств, а процессы, представленные на рис. 1.9, в, г, – для большого числа измерительных устройств, основанных на прямом преобразовании. Кривая на рис. 1.9, в представляет собой экспоненту, а величина Т (подкасательная) называется постоянной времени. Она определяет собой время, за которое вы­ходной сигнал достиг бы нового установившегося значения, если бы изменялся с постоянной скоростью, равной скорости в момент Скачкообразного изменения входного сигнала.

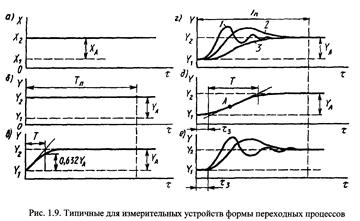
Постоянная времени используется для характеристики динамических свойств измерительных устройств. Проведение касательной и кривой переходного процесса сопряжено с погрешностями, поэтому значения постоянной времени определяют как интервал времени, за который выходной сигнал изменяется на 0,632 от своего при­ращения Y_A (рис. 1.9, в). Корректность такого определения легко доказывается математически.

Колебательное динамическое звено, а следовательно, и измерительное устройство, в котором имеет место переходный процесс (рис. 1.9, г), можно рассматривать как соединение двух апериодических звеньев с постоянными времени Т ₁ и Т ₂. При этом в зависи­мости от соотношений Т ₁ и Т ₂ переходный процесс будет различен. Если (Т ₁/ Т ₂) < 2, то он имеет форму кривых 1 и 2, а при (Т ₁/ Т ₂) ≥ 2 – форму кривой 3 (рис. 1.9, г).

---

Дата добавления: 2016-01-04; просмотров: 80; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!