Будь-які 4 вектори-лінійно залежні.

5. Аксіоми відкладання векторів:

5.1Для будь-якої т. А і В будь – якого вектора , існує єдина т. В, що = .

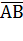5.2 Для будь-яких 3-х точок справедлива рівність + .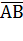

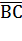13. Модель — це прообраз, опис або зображення якогось об’єкта.

Мат. модель — це модель, що описує об’єкт, явище чи процес мовою математики.

Моделювання - це наукова теорія побудови і реалізації моделей, за допомогою яких досліджуються явища і процеси в природі і суспільному житті. Досліджуючи будь-яке явище (процес, об'єкт), ми будуєм у свідомості їх моделі.

Математична структура роду Т - це множ. Т тверджень (теорем), кожне з яких є логічним наслідком аксіом системи суми, які визначають Т.

Припустимо, що нам дана деяка система множин: М1, М2,...., Мn (n≥1). Позначимо через деякі відношення на цій системі. Ці відношення не будемо фіксувати як певні підмножини декартового добутку ММ.... Мn, а лише будемо вимагати, щоб вони мали задані властивості: (1), які ми явно формулюємо. Позначимо через Т множину всіх систем δ={р,...,р } відношень, кожна з яких має задані властивості (1). Якщо Т ≠ Ø, то говорять, що елемент δ Т визначає на множинах М,..., М структуру роду Т. Явно сформульовані властивості (1), що визначають множину Т, називаються аксіомами роду Т, а множини М,..., М – базою структур роду Т. Всім структурам одного і того ж роду дають спеціальну назву: структура групи, структура -вимірного евклідового простору і т.д.

База складається з однієї множини М1≠Ø, система відношень складається з одного відношення р1, яке повинно задовольняти чотирьом аксіомам: α: р – алгебраїчна операція на множині М; α: p(p(a, b),c) = p(a, p(b, c)), a, b, c М( асоціативність); α: e М: (а,е) = р1(е,а) = а; а М (існування нейтрального елемента); α: a М1: (існування елемента, симетричного елементу). Множині, на якій визначена структура даного роду, дають спеціальну назву. В цьому прикладі говорять: «М – група, або більш повно: на множині М визначена структура роду структури групи».

14-15. Система аксіом Ω простору П називається несуперечливою, якщо в ній та її наслідках немає тверджень, які заперечують одне одного. Першою вимогою, що ставиться до системи аксіом Ω простору П, є вимога її несуперечливості. Ідея доведення несуперечливості даної системи аксіом заснована на такій думці, що коли існує хоча би одна така галузь об’єктів, деякі відношення між якими задовольняють даній аксіоматиці, то остання не може містити логічних протиріч. Означення 2. Моделлю системи аксіом Ω називається конкретна множина конкретних об’єктів, між якими встановлюються конкретні відношення, які задовольняють аксіоми системи Ω. Таким чином, доведення несуперечливості системи аксіом зводиться до доведення існування хоча би однієї моделі (або інтерпретації) системи аксіом.

Незалежність системи аксіом: Аксіома ω системи аксіом Ω простору П називається незалежною в Ω, якщо вона не є наслідком останніх аксіом системи Ω. Система аксіом Ω називається незалежною, якщо всі її аксіоми незалежні. Для доведення незалежності системи аксіоми потрібно побудувати стільки моделей, скільки є аксіом в системі, причому кожна модель повинна реалізувати всі аксіоми, крім тієї, яка досліджується на незалежність.

Повнота системи аксіом: Повнота системи аксіом означає, що на основі цієї системи по відношенню до кожного твердження Т, що стосується понять даної теорії, можна розв’язати питання: істинне воно чи хибне. Таким чином, відносно повної системи аксіом кожне твердження даної теорії належить або до I-ої або до II-ої категорії. Тверджень III-ої категорії не існує. Прикладами неповної системи аксіом є система постулатів «Начал» Евкліда.

Аксіоматична теорія, будь-які дві моделі якої ізоморфні, називаються категоричною. Для категоричної теорії кожне висловлення, яке істинне в одній з її моделей, буде істинним і в будь-якій іншій моделі. Евклідова геометрія є категоричною теорією. Прикладом некатегоричної теорії є теорія груп.

Дві різні моделі однієї і тієї ж системи аксіом називаються ізоморфними, якщо між основними об’єктами цих моделей можна встановити взаємно однозначну відповідність.

16-17. Підручник О. В. Погорєлова побудований за традиційною схемою. Особливість цієї схеми полягає в тому, що ознаки рівності трикутників розглядаються на початку курсу і є основним засобом у доведеннях теорем і розв'язуванні задач. Його побудовано на дедуктивній основі, хоч і не строго аксіоматично. Виклад теоретичного матеріалу ґрунтується на семи первісних поняттях. Шість із них - планіметричні, які переходять в стереометрію (точка, пряма, довжина відрізка, градусна міра кута, відношення «належати» для точок і прямих і «лежить між» для трьох точок прямої), і одне вводиться в стереометрії - поняття «площина».

Основні властивості не означуваних понять описують дев'ять аксіом планіметрії які переходять у стереометрію (аксіоми IV, VII, VIII і IX з незначними уточненнями), і три аксіоми стереометрії. Чотири аксіоми планіметрії (IV, VII, VIII, IX), які переходять разом з усіма іншими в стереометрію, потребують уточнення, оскільки в просторі існує не одна, а безліч площин. Після уточнення вони формулюються так:

IV. Пряма, що належить площині, розбиває цю площину на дві півплощини.

VII. Від пів прямої на площині, яка її містить, в задану півплощину можна відкласти кут з даною градусною мірою, меншою за 180°, і тільки один. VIII. Хоч би яким був трикутник, існує рівний йому трикутник у даній площині в заданому розміщенні відносно даної пів прямої в цій площині. Підручник має близько 1200 задач. Система задач посібника передбачає розв'язування в класі близько половини задач, на що в середньому має витрачатись близько 50 % сукупного навчального часу уроку.

Л.С Атанасяна: основними об’єктами в ній є точка,пряма,площина; основними відношеннями між основними об’єктами – належність, лежати між,накладання, міра відрізка. Використовуються загально математичні поняття множина,число та ін. формування аксіом містять як планіметричні так і стереометричні твердження. Аксіоми розбиті на групи. Аксіоми 1 групи характеризуються взаємним розміщення точок, прямих і площин. 2 група аксіом належить до понять накладання і рівності фігур. 3 група аксіом пов’язана з вимірюванням відрізків. 4 група аксіом – це аксіоми паралельності.

О. Д. Александрова: формулювання аксіом у цих посібниках передбачає що учням відома арифметика дійсних чисел і понять додатної величини. Основні поняття: точка і пряма. Основні відношення: належність,лежати між. Система аксіом розбита на 5 груп: 1. Акс. належності. 2. Акс. порядку. 3. Акс. відстані. 4. Акс. рухомості. 5. Акс. паралельності Евкліда. Є також 5 аксіом стереометрії.

18. М.І.Лобаче́вський - відомий російський математик, творець неевклідової геометрії. Народився в Нижньогородській губернії. Після смерті батька разом з сім'єю переїхав у Казань. Там Лобачевський закінчив гімназію (1802—1807), а потім щойно заснований Казанський імператорський університет, якому віддав 40 років життя. Великий вплив під час навчання в університеті на Лобачевського справив Мартин Бартельс — друг і вчитель великого німецького математика Гауса. Він взяв шефство над бідним, але обдарованим студентом. У 1819 році в Казань приїхав ревізор (М. Л. Магницький), який надав вкрай негативний висновок про стан справ в університеті. Лобачевського призначили деканом фізико-математичного факультету. У ці роки він пише підручники з алгебри та геометрії; перший з них було цензуровано за використання метричної системи мір, а другий взагалі не допустили до друку. У 1826 р. Магницького було усунуто з посади попечителя за зловживання. Призначається новий попечитель (М. Н. Мусін-Пушкін). Лобачевський обирається ректором університету. Він з головою занурюється в господарські. Багато що він робить власними руками. Читає науково-популярні лекції з фізики для населення. Одночасно він невтомно розвиває та шліфує справу свого життя - неевклідову геометрію. У 1832 році Лобачевський одружується на Варварі Олексіївні Моісеєвій. У подружжя народилось семеро дітей. Лобачевський був ректором Казанського університету в період з 1827 по 1846 роки, пережив епідемію холери (1830) та сильну пожежу (1842), що знищила половину Казані. Зусиллями Лобачевського Казанський університет стає першокласним, авторитетним і добре оснащеним навчальним закладом, одним з найкращих в Росії. 20 листопада 1845 року Лобачевського було вшосте затверджено на посаді ректора на наступні чотири роки. Головну працю вченого, «Пангеометрія» записують під диктовку учні сліпого вченого у 1855 році. Збереглися студентські записи лекцій Лобачевського (від 1817 року), де ним робилась спроба довести п'ятий постулат Евкліда, але в рукопису підручника «Геометрія» (1823) він вже відмовився від цієї спроби. 1826 року Лобачевський представив для друку в Записках фізико-математичного відділу твір: «Стислий виклад початків геометрії зі строгим доведенням теореми про паралельні » (на французькій мові). Але видання не відбулося. Рукопис та відгуки не збереглися, проте сам твір було включено Лобачевським в його працю « Про початки геометрії » (1829—1830), надрукований в журналі «Казанский весник». Цей твір став першою в світовій літературі серйозною публікацією по неевклідовій геометрії або геометрії Лобачевського. Лобачевський вважає аксіому паралельності Евкліда довільним обмеженням. Як згодом з'ясувалося, Гаус і сам потайки розвивав неевклідову геометрію, проте так і не наважився опублікувати що-небудь на цю тему. Ознайомившись з результатами Лобачевського, він побічно висловив свою симпатію до ідей вченого: рекомендував обрати Лобачевського іноземним членом-кореспондентом Геттингенського королівського товариства. Лобачевський помер невизнаним. Через декілька десятиріч ситуація в науці докорінно змінилася. Більшу роль у визнанні праць Лобачевського відіграли дослідження Е. Бельтрамі (1868), Ф. Клейна (1871), А. Пуанкаре (1883) та інші.

19. Одним з найважливіших його досягнень стало перше доведення несуперечності геометрії Лобачевського; для цього він збудував її інтерпретацію в евклідовому просторі (дивись модель Клейна). Він побудував приклад односторонньої поверхні — «пляшку Клейна». За площину приймається будь-якої коло (рис. 2.1), за точки - точки належать цьому колі, за прямі - хорди - звичайно, з виключенням решт, оскільки розглядається тільки внутрішність круга. За переміщення приймаються перетворення кола, що переводять його в себе і хорди - в хорди. Відповідно, "конгруентними" називаються фігури, перекладні один в одного такими перетвореннями.

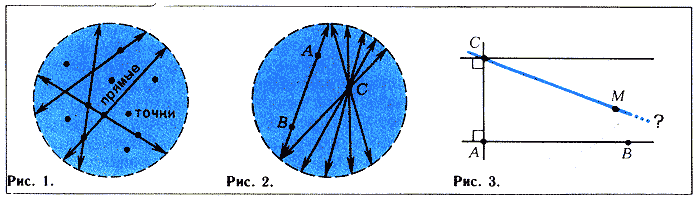
Очевидно, що в межах певної частини площині (кола), як би ця частина не була велика, можна провести через дану точку С безліч прямих, не перетинають даної прямої. Всередині кола будь-якого кінцевого радіуса існує безліч прямих (тобто хорд), що проходять через т. С і не зустрічаючих прямий АВ. Будь-яка теорема планіметрії Лобачевского є в цій моделі теоремою геометрії Евкліда і, назад, всяка теорема геометрії Евкліда, що говорить про фігури всередині даного кола, є теоремою геометрії Лобачевського. Це загальне твердження доводиться перевіркою справедливості в моделі аксіом геометрії Лобачевського. Тому, якщо в геометрії Лобачевського є протиріччя, то це ж протиріччя є і в геометрії Евкліда.

Далі, всяка теорема геометрії Лобачевського описує в моделі Клейна деякі факти, що мають місце всередині кола. Саме факти, якщо ми беремо не абстрактний коло, а реальний коло і реальні хорди і інтерпрітіруем теореми як твердження про ці реальні речі, взяті, звичайно, з тією точністю, яка доступна для наших побудов. Таким чином, геометрія Лобачевського в моделі Клейна має цілком реальний сенс з тією точністю, з якою взагалі має сенс геометрія в застосуванні до реальних тіл.

20. Система аксіом Лобачевского:

1. Належності:

1.9 Які б не були т. А і В існує пряма що проходить ч/з ці точки.

1.10 Які б не були2 т. А і В існує не більше 1-ї прямої що проходить ч/з ці точки.

1.11 На кожній прямій лежить хоча б 2 точки. Існують хоча б 3 точки які не лежать на 1 прямій.

1.12 Які б не були 3 точки що не лежать на 1 прямій існує площина яка проходить ч/з ці точки. На кожній площині лежить хоча б 1 точка.

1.13 Які б не були 3 точки які не лежать на 1 прямій існує не більше 1 площини яка проходить ч/з ці точки.

1.14 Якщо 2 т. А і В прямої а лежать в площині L, то кожна цієї прямої лежить в L.

1.15 Якщо 2 площини мають 1 спільну точку то вони мають хоча б іще 1 спільну точку.

1.16 Існують хоча б 4 точки які не лежать в 1 площині.

2. Порядку:

2.1 Якщо А-В-С і А,В,С – різні точки 1 прямої то точки С-В-А.

2.2 Які б не були 2 т. А і В існує хоча б 1 т. С на АВ така, що А-В-С.

2.3 Серед довільних 3 точок прямої існує не більше 1 точки яка лежить між 2 іншими.

2.4 (Акс. Паша.) Нехай 3 т. А,В,С не лежать на 1 прямій а лежать АВС і не проходить ч/з жодну з точок тоді, якщо пряма а проходить ч/з точку відрізка АВ, то вона проходить також ч/з точку відрізка АС або ВС.

3. Конгруентності:

3.1 Якщо заданий відрізок АВ і промінь який виходить із т. А’ то існує В’ яка належить даному променю така що АВ конг. А’В’.

3.2 Якщо А’В’ конг. АВ і А’’В’’ конг. АВ, то А’В’конг. А’’В’’.

3.3 Нехай А-В-С і А’-В’-С’, АВ конг. А’В’, ВС конг. В’С’, тоді АС конг. А’С’.

3.4 Нехай задано кут hk і прапор (o`, h`, x`), тоді на півплощині х’ існує один єдиний промінь K`, який виходить з т. O`такий, що кут hk конг. куту h`k`.

3.5 Нехай 3 точки А’В’С’ не лежать на одній прямій, А’В’С’ – не лежать на одній прямій, якщо при цьому АВ конг. А’В’, АС конг. А’С’, кут ВАС конг. В’А’С’, тоді кут АВС конг. куту А’В’С’.

4. Неперервності:

4.1 (акс. Архімеда) Нехай задано АВ і СД, тоді АВ існує скінчена множена таких точок А1…..Аn, що будуть виконувати умови:

1. А-А1-А2.

2. АА1 конг. А1А2 конг…..конг. Аn-1 Ап конг.СД.

3. А-В-Аn.

4.2 (акс. Кантера) Нехай на довільній прямій а задано нескінчена послідовність відрізків А1В1, А2В2… з яких кожний наступний лежить в середині і крім того для довільного СД знайдеться таке n, що AnBn<СД, тоді існує єдина т. М, яка належить кожному з відрізків послідовності.

5. Паралельності: Нехай а- довільна пряма, А – точка, яка їй не належить,тоді в площині, яка визначається т. А і прямою а, існує не менше 2-х прямих, що проходить ч/з т. А і не перетинає пряму а.

21. Паралельними (рівнобіжними) прямими називають прямі, котрі лежать в одній площині і або збігаються, або не перетинаються. В геометрії Лобачевського в площині через точку 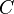що лежить поза даною прямою 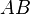проходить нескінчена кількість прямих, що не перетинають 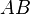. З них паралельні до 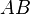називаються тільки дві. Пряма 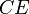називається рівнобіжною (паралельною) до прямої 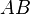в напрямку від 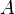до 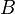, якщо: т. 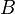і 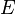лежать по одну сторону від прямої 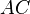; пряма 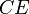не перетинає пряму 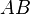, але всякий промінь, що проходить всередині кута 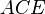, перетинає промінь 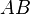. Аналогічно означається пряма, рівнобіжна до 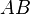в напрямку від 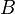до 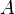. Всі інші прямі, що не перетинають дану, наз. ультрапаралельними.

Про властивості: В евклідовій площині відстань між паралельними прямими є величиною сталою. Ця властивість у площині Лобач. не зберігається. Тут має місце така теорема. Т: Дві паралельні прямі на площ. Лобач. асимптотично зближаються в бік паралельності і необмежено розходяться в протилежний бік. В евклідовій площині дві паралельні прямі мають безліч спільних перпендикулярів. У площині Лобач. нічого такого не спостерігається. Тут має місце така теорема. Т: У площ. Лобач. збіжні в паралельні прямі не мають спільного перпендикуляра а розбіжні прямі можуть мати лише один спільний перпендикуляр.

22. Лема: якщоАВ ІІ СД то існує вісь симетрії прямих АВ і СД. Довед: Візьмемо т. РQ відповідно на прямих АВ і СД. Нехай промінь hk- бісектриси кута QРВ і кута ДQР. Оскільки за умови АВ ІІ СД то промінь перетинає QД в т. І.покажемо що т. S є рівно віддаленою від прямих АВ і СД. Рогзл. Трикутник Н3РS. З рівності трик. Н1SР = трик. Н3SР, випливає SН1 = SН3. Пряма Д що проходить т.S і є бісектрисою кута Н1SН2 є віссю симетрії прямих АВ і СД. Лема доведена. Теор.: якщо АВ і СД на площині Лобач. причому АВІІСД, то і СДІІАВ. Теор.: 2 прямі паралельні 3 в одному і тому ж напрямку паралельні між собою і в тому ж напрямку. Озн. 2 ненаправлені прямі наз. паралельними, якщо на них можна вибрати таким чином напрями щоб вони були паралельними. Озн. 2 прямі на площ. Лобач. наз. Розбіжними або сверх паралельні якщо вони не перетинають або паралельні. Теор.: 2 прямі що мають спільний перпендикуляр розбігаються. Довед: Вони не можуть бути гострими бо вони прямі. Насл.: на площ. Лобач. не існує спільного пенепен. До двох паралельних прямих. Заув: дві прямі не можуть мати більше ніж один спільний перпендикуляр. Лема: Нехай промінь РР` і QQ` лежать в одній на півплощині межею РQ. При цьому кут Q` РQ є прямий, а кут QР Q` тупий або прямий, і нехай т. М є бігуча точка променя РР’. і нехай h є проекція цієї точки на QQ’ тоді ф-я Мh залежить f (МС) є ф-я монотонно нескінченно зростаючою. Коли т. М віддаляється в т. Р напрямку паралельності то відстань Нh прямує до 0.тому паралельні прямі на площ. Лобач. асиметрично наближається один до одного.

23. Нехай а – деяка пряма, і А – точка, яка не лежить на цій прямій. Нехай АР – перпендикуляр до прямої а і a ' - пряма, що проходить через А і паралельна а (рис.) Позначимо через гострий кут, який пряма а ' утворює з перпендикуляром АР. Кут називається кутом паралельності прямої а ' в точці А по відношенню до прямої а.

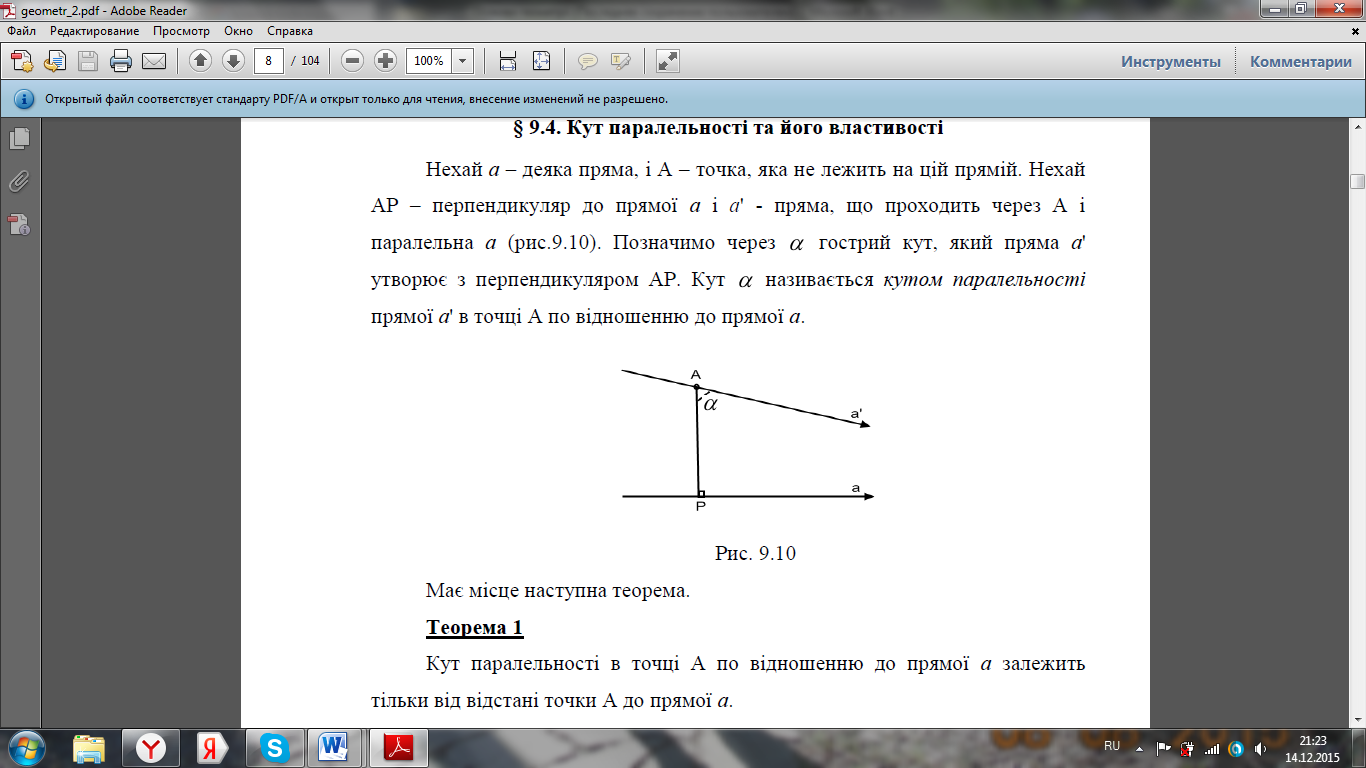Має місце наступна теорема. Т1: Кут паралельності в точці А по відношенню до прямої а залежить тільки від відстані точки А до прямої а. Доведення. Нехай дані дві прямі а і а ' і дві точки А і А' віддалені від прямої а і а ' на одну і ту ж відстань. Через точки А, А' проводимо прямі b, b', які відповідно паралельні прямим а і а ' вправо. Нехай і - кути паралельності в точках А і А' відносно прямих а і а ' (рис.9.11)

Функція Лобачевського П(х), задана на проміжку (0;+∞), неперервна на цьому проміжку, строго спадна.

24. На площ. Лобач. Сума кутів трикутника не може бути рівною 2d. Вона не може бути й більшою за 2d, бо це суперечить абсолютній геометрії. Тому на площ. Лобач. сума кутів трикутника менша 2d. Виявляється що такого конкретного числа для всіх трикутників Лобач. просто не існує. Тут справджується така теорема. Т: Сума кутів трикутника в геом. Лобач. є величина змінна і залежить від форми і розмірів трикутника. Різниця між числом π і сума кутів трикутника наз. кутовим дефектом трикутника, її позначають D(дельта). У геом. Евкліда кутовим дефектом трикутника=0, а в геом. Лобач. кутовий дефект – змінна додатна величина змінюється в межах від 0 до π. Можна довести що геом. Лобач. площа трикутника пропорційна кутовому дефекту. Але в геом. Лобач. не існує подібних нерівних трикутників. Т: На площ. Лобач. не існують нерівних трикутників. З цієї теореми, як наслідок випливає таке твердження: якщо на площ. Лобач. три кута одного трикутника відповідно дорівнюють трьом кутам відповідного трикутника, то такі трикутники рівні. Ця теорема дає нову четверту ознаку рівності трикутників якої не має в абсолютній геометрії і в геометрії Евкліда. Т: У площ. Лобач. не навколо будь-якого трикутника можна описати коло.

25. На площ. Лобач. існує три типа пучків: 1. Пучок прямих, що перетинаються, тобто множина всіх прямих площ., що проходять ч/з одну точку – центр пучка. 2. Пучок розбіжних прямих, тобто множина всіх прямих площ., перпендикулярних до даної прямої. 3. Пучок паралельних прямих - множина прямих, яка складається з деякої напрямленої прямої і всіх напрямлених прямих, які паралельні даній. Ясно що якщо задано пучок то ч/з будь-яку точку площини проходить одна і тільки одна пряма пучка.

Коло- наз. фігура яка складається із всіх точок площини, рівновіддалених від даної точки. Слідвідмітити теорему про те що будь-яка пряма, що лежить в площині кола, перетинається з ним не більш ніж у двох точках. Властивості: 1. Коло симетричне відносно будь-якої своєї вісі. 2. В кожній точці кола існує дотична, яка пенпендикулярна до вісі, що проходить ч/з точку дотику. Враховуючи цю властивість ми можемо говорити що коло перптинає свої вісі під прямим кутом або що коло є ортогональна траєкторія пучка прямих з центром у кола. Також ще дві властивості кола: 3. Пряма що містить хорду кола відмінну від діаметру, єсічною рівного нахилу до осей, що проходять ч/з кінці хорди. 4. Серединний пенпендикуляр до будь-якої хорди кола є його віссю.

26. Еквідістантою наз. фігуру яка з усіх точок півплощини з межею и, рівновіддалених від цієї прямої. Пряма и наз. базою еквідістанти, а пенепендикуляр проведений з будь-якої точки еквідистанти на базу є висотою. Вмсотою також наз. довжина h цього пенпендикуляру. З еквідістантою пов'язаний пучок розбіжнихпрямих множина всіх прямих, перпендикулярних до бази еквідістанти. Прямі цтого пучка наз. осями еквідистанти. Багато властивостей аналогічні до властивостей кола. Т: Будь-яка пряма, що лежить в площині еквідистанти, перетинається з еквідистантою не більше ніж у двох точках. Властивості: 1. Еквідистанта симетрична відносно будь-якої вісі. 2. В кожній точці еквідистанти існує дотична, яка пенпендикулярна до осі проведеної ч/з точку дотику. 3. Будь-яка пряма, що містить хорду еквідистанти є січною рівного нахилу до осей що проходять ч/з кінці хорди. 4. Серединний пенпендикуляр до будь-якої хорди еквідистанти є її віссю.

Орицикл. До того як дати означення доведемо слідуючи лему. Лема: ч/з кожну точку однії з двох паралельних прямих проходить одна і тільки одна січна рівного нахилу до цих прямих. Властивості орицикла аналогічно властивостям кола та еквідистанти. Т: Довільнапряма що лежить в площині орицикла, перетинає орицикл не більше ніжу 2-х точках.

27. Т: Якщо два серединних пенпендикуляри до сторін трикутника перетинаються, тоі тратій серединний пенпенликуляр проходить ч/з цю точку перетину. Доведення: у геом. Евкліда кожна точка серединного пенпендикуляра відрізка рівновіддалена від його кінців. Це твердження доводиться на основі рівності трикутників, тому воно справедливе і на площ. Лобач. Наслідок: якщо два серединних пенпендикуляра до сторін трикутника перетинаються у т. О то навколо такого трикутника можна описати коло із центром у т. О. Т: якщо два серединних пенпендикуляри до сторін трикутника розбіжні то і серединний пенпендикуляр до третьої сторони трикутника розбіжний з двома першими і всі вони мають єдиний спільний пенпендикуляр, причому всі вершини трикутника рівновіддалені від нього. Наслідок: якщо два серединних пенпендикуляри до 2-х сторін трикутника розбіжні то навколо такого трикутника можна описати еквідистанту. Т: Якщо два серединні орієнтовані в один бік до сторвн трикутника пенпендикуляри паралельні, то і серединний пенпендикуляр до третьої сторони трикутника паралельний двом першим. Наслідок: якщо серединних пенпендикуляра до 2-х сторін трикутника паралельні в даному напрямку, то навколо такого трикутника можна описати орицикл. З теорем випливає, що в площ. Лобач. навколо кожного трикутника можна описати одну з трьох ліній або коло, або еквідистанту або орицикл.

28. 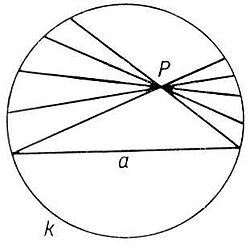Бельтрамі показав, що в евклідовому просторі є поверхні постійної від’ємної кривини – псевдосфери. Кривина кривої визначає міру відхилення кривої від дотичної в даній точці. Модель Бельтрамі – Клейна розглядається у вигляді кругу з радіус = 1. Цей круг абсолютний, а коло абсолют. В цій реалізації можна означити ч/з поняття евклідової площини. Введемо позначення: Л-точка (точка ПЛ), Л-пряма (пряма ПЛ), Л-площина(площа Лобач.), означення основних понять геом. Лобач. Л-точками є евклідові точки відкритого абсолютного круга. Точка абсолюта до Л-точок не належать, їх називають невласними точками, а точки, що лежать зовні абсолюта, - ідеальними. Л- прямими наз. відкриті хорди абсолюта; Л-площиною – відкритий абсолютний круг. При означенні основних понять Лобач. ч/з основні поняття геом. Евкліда легко переконатися у виконані всіх аксіом геом. Лобач. у розумінні понять геом. Лобач. це означає що на кожній Л-прямій існують принаймні дві Л-точки і існують три кожні Л-прямі які не належать одній Л-прямій. Оскільки відношення «лежати між» для точок прямої таке ж як і для точок хорди абсолютного круга, а це відношення має такий самий зміст і в розумінні Лобач. то вимоги аксіом порядку виконуються в даній реалізації для Л-точок і Л-прямих. Таким чином у реалізації Бельтрамі – Клейна виконується всі аксіоми планіметрії Лобач. Тому планіметрія Лобач. несуперечлива настільки, наскільки несуперечлива планіметрія Евкліда (у реалізації Бельтрамі – Клейна одночасно з доведення несуперечливості геом. Лобач. доведено і незалежність 5 постулату).

29. Реалізація Пуанкаре акс. планіметрії Лобач. на евклідовому крузі – абсолютному крузі. Ця інтерпретація аналогічна інтерпретації Бельтрамі – Клейна, але роль Л- прямих відіграють дуги евклідових кіл, ортогональних з абсолютом. Нехай довільна горизонтальна пряма т розбиває площу Евкліда на дві півплощини. Одну з них назвемо верхньою (над прямою т). Введемо означення основних понять планіметрії Лобач. Л-точками назвемо евклідові точки верхньої півплощини. Точки прямої т не належать до Л-точок. Л-прямими назвемо евклідові півкола, що лежать у верхній півплощини і ортогональні до прямої т (тобто мають центр на прямій т), а також евклідові пів прямі верхньої півплощини, перпендикулярні до прямої т. Запропонована реалізація аксіом геом. в образах планіметрії Евкліда є модель планіметрії Лобач. тому планіметрія Лобач. несуперечлива настільки, наскільки несуперечливою є планіметрія Евкліда. Звідси також випливає що акс. паралельності Евкліда і акс. паралельності Лобач. не є наслідками акс. абсолютної геом., вона не залежить від акс. абсолютної геом.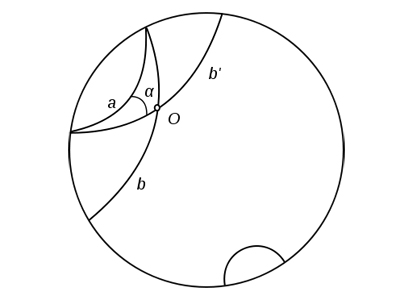

30-31. Сферою наз. фігура яка складається з усіх точок простору, рівновіддалених від даної точки. Ця точка наз. центром сфери. Відстань від точок сфери наз. радіусом сфери. Відрізки які сполучають 2 точки сфери і проходять ч/з центр, наз. діаметрами, а кінці діаметра – діаметрально протилежними точками. Фігура наз. сферичною, якщо всі її точки лежать на одній і тій самій сфері. Сферична геом. вивчає геометричні властивості фігур, розміщених на сфері. Основними поняттями сферичної геометрії є поняття точки і великого кола сфери. Сферичні трикутники наз. фігура, утворена трьома дугами великих кіл,які перетинаються в трьох точках. Дуги що утворюють трикутники, наз. сторонами, а точки їх перетину – вершинами трикутника. Слід зазначити, що в той час, коли сторони плоского трикутника є відрізками прямої і вимірюються лінійними одиницями, сторони одиницями – градусами, або радіанами. У стереометрії доводяться такі властивості плоских кутів тригранного кут: 1. Кожний з плоских кутів тригранного кута менший від суми 2-х інших його плоских кутів але більший за їх різницю. 2. Сума трьох плоских кутів тригранного кута більша від нуля і менша від 360 Градусів. Т: Кожна сторона сферичного трикутника менша від суми двох інших і більша за їх різницю. Т: сума сторін сферичного трикутника завжди менша 360 гр. і більша від 0. Сума кутів СТ: Т: У будь-якому сферичному трикутнику різниці суми двох будь-яких кутів і третього завжди менша двох прямих кутів. Т: Убудь-якому сферичному трикутнику сума кутів завжди менша від 540 Гр. і більша від 180 Гр. Наслідок: Сума кутів у сферичному трикутнику є величина змінна і завжди більша від 180 Гр. Зауважимо що у сферичному трикутнику поняття бісектриси, медіани, висоти, співвідношення між сторонами і кутами мають такий зміст як і в трикутниках на площині. Зокрема мають такі твердження: 1. Проти рівних сторін сферичного трикутника лежать рівні кути і навпаки. 2. У будь-якому сферичному трикутнику проти більшого кута лежить більша сторона і навпаки. 3.у рівнобедреному сферичному трикутнику кути, що лежать проти рівних сторін, рівні.

32. Озн: Сукупність 2-х діаметрально протилежних точок і двох півкіл, кінцями яких є ці точки наз. сферичним двокутником. Півкола, які утворюють двокутник наз. його сторонами, а їх спільні кінці – його вершинами. Т: Площа сферичного двокутника пропорційна величині його кута. Доведення: двокутники кути яких рівні між собою рівні а тому за властивістю інваріантності площі, мають одну й ту саму площу. Якщо кут деякого двокутника = сумі кутів 2-х інших двокутника, то площа першого = сумі площ 2-х інших двокутників (за властивістю адитивності). Т: Площа сферичного трикутника пропорційна до його сферичного надвишку. Наслідок: оскільки для сферичного трикутника α+β+µ>π, то сферичний надлишок завжди додатний.

Географічна сферична система координат задається двома взаємно перпендикулярними великими колами CABD та PLCP1DT. Коло CABD називається екватором, а півколо PLCP1 − початковим меридіаном. Координатна сітка цієї системи утво- рюється паралелями – колами малих кіл, що паралельні екватору, та меридіанами – півколами великих кіл, що перпендикулярні до екватора. Кожний меридіан з’єднує північний P та південний P1 полюси.

Написать від руки.

34. Поняття руху на сфері можна ввести аналогічно до відповідного поняття на площ.: рухом на сфері наз. таке перетворенення сфери при якому зберігається відстань між точками. Отже, якщо фігура F перетворюється у фігуру F` на сфері рухом то при цьому будь-які дві точки А і В фігури F переходять у такі точки А і В фігури F`, що АВ=А`В`. Основні властивості рухів на площ. Переносяться відповідно на рухи сфери, але рухи на сфері мають деякі властивості, яких не мають рухи на площ. Зокрема оскільки відстань між двома діаметрально протилежними точками сфери одна й та сама і = 2 радіусам сфери, то при будь-якому радіусі сфери діаметрально протилежні точки переходять у діаметрально протилежні точки сфери. Найпростішими рухами сфери є поворот сфери навколо будь-якої осі, що проходить ч/з центр сфери, симетрія сфери відносно будь-якої площини, що проходить ч/з центр сфери, симетрія сфери відносно сфери відносно її центр. Існують 4 ознаки рівності сферичних трикутників. Перші 3 ознаки формулюються як і для плоских трикутників, крім того, рівними є трикутники з різними відповідними кутами доведення ознак рівностей сферичних трикутників розміщених на одній сфері або на двох сферах однакового радіуса проводиться за допомогою ознак рівності відповідних тригранник кутів з вершинами в центрі сфери.

35. Бернгард Ріман — німецький математик, механік і фізик. Нахили до математики виявлялися у молодого Рімана ще в дитинстві, але поступаючись бажанню батька, в 1846 році він вступив до Геттінгенського університету для вивчення філології та богослов'я. Однак тут він слухає лекції К. Ф. Гаусса і приймає остаточне рішення стати математиком. У 1851 році Ріман захищає дисертацію «Основи теорії функцій комплексної змінної», де вперше було введено поняття, пізніше здобуло популярність як «ріманова поверхня». У 1854-1866 роках він працює в Геттінгенському університеті. У 1857 році Ріман опублікував класичні праці з теорії абелевих функцій і аналітичної теорії диференціальних рівнянь і був переведений на посаду екстраординарного професора Геттінгенського університету. 1862 рік: Одружився на Ельзі Кох, подрузі покійної сестри. У них народилася дочка Іда. На жаль, незабаром після одруження Ріман застудився і серйозно захворів. 1866 рік: Ріман помер в Італії від туберкульозу у віці неповних 40 років. Дослідження Рімана відносяться до теорії функцій комплексного змінного, теорії чисел, геометрії, математичної і теоретичної фізики, теорії диференціальних рівнянь. Слідом за Коші, Ріман розглянув формалізацію поняття інтеграла і ввів своє визначення — інтеграл Рімана. Система аксіом Рімана. 1.Акс. належності:

1.1 Які б не були 2 т. А і В існує пряма що проходить ч/з ці точки.

1.2 Які б не були 2 т. А і В існує не більше 1-ї прямої що проходить ч/з ці точки.

1.3 На кожній прямій лежить хоча б 2 точки. Існують хоча б 3 точки які не лежать на 1 прямій.

1.4 Кожна пара прямих що лежать в одній площині перетинаються.

2.Акс. розміщення:

2.1 Якщо А,В ÷ С,Д то 4-и т. А,В,С,Д різні і належать одній прямій а.

2.2 Якщо А і В – різні точки прямої а, то на цій прямій існують такі дві точки М,Р що А,В ÷ М,Р.

2.3 Якщо А,В ÷ С,Д то С,Д÷ А,В.

2.4 Якщо А,В ÷ С,Д то А,В ÷Д,С.

2.5 Якщо А,В÷С,Д то не може бути А,С÷В,Д.

2.6 Якщо А,В,С,Д- різні точки прямої то справджується одне і тільки одне з відношень: А,В ÷ С,Д або А,С ÷В,Д або А,Д÷В,С.

2.7 Якщо А,В÷С,Д і А,С÷В,Е то А,С ÷Д,Е.

2.8 Якщо 4-и прямі пучка перетинають дві будь-які прямі відповідно в точках А,В,С,Д і А1,В1,С1,Д1, і якщо А,В÷С,Д то А1,В1÷С1,Д1. ≡

3. Акс. Конгруентності( ≡):

3.1 Кожен відр. ≡ сам собі.

3.2 Якщо 1 відр. ≡ 2 то 2 ≡1.

3.3 Якщо 1 відр. ≡ 2 а 2 ≡ 3 то1≡ 3.

3.4 Якщо ≡ 2 відр. Випливає конгруентність їх взаємно розташованих відр.

3.5 Кожен відр. не≡ своїй частині.

3.6 Для кожної точки прямої існує її протилежна.

3.7 Всі напівпрямі ≡ між собою.

3.8 Якщо АВ≡А’В’ і т. С – внут. Точка АВ, то в середині А’В’ існує т. С’, А’В’≡АС і С’В’≡СВ.

4. Акс. Неперервності:

4.1 Кожна точка відр. потрапляє в один із цих класів.

4.2 Кожен клас не порожній.

4.3 Якщо т.Х належить першому класу, а т. У, то т. Х завжди є внут. точкою відр. АХ, тоді на відр. АВ існує т. С, що будь-яка внут. точка АС належить першому класу, будь-яка точка СВ належить другому класу.

36. В той час, як у евклідовій геометрії існує постулат про єдиність прямої, що проходить через дану точку і не перетинає дану пряму, а в геометрії приймається одне з заперечень цього постулата: допускається, що таких прямих існує безліч, - в геометрії Рімана існує інше заперечення: в цій геометрії будь-яка пряма перетинає іншу. В геометрії Рімана пряма визначається двома точками, площина - трьома точками, дві площини перетинаються по прямій. Ріман додав до числа аксіом слідуюче твердження: кожна пряма,яка лежить з даною прямою в одній площині, перетинає цю пряму. Ріман, розвиваючи свою систему повинен був ще сильніше змінити евклідову аксіоматику, ніж Лобач.
Розміщення прямих на площині Рімана ще в одному відношенні принципово відрізняється від розміщення прямих на площині Евкліда, чи на площині Лобачевського, а саме: пряма не ділить площину Рімана на дві частини. Це означає, що якими б не були пряма α і дві точки А і В, які належать цій прямій, завжди можна сполучити точки А і В відрізком так, що цей відрізок не перетне прямої α.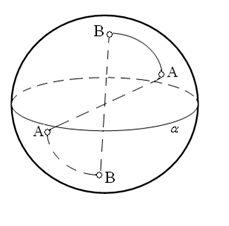

37. Навідміну від Евклідової площини, яка має нульову кривизну, та площини Лобачевського, яка має постійну негативну кривизну, існують і площини, що мають позитивну кривизну. Саме на цій площині й існують трикутники, які мають сума кутів трикутника більшу за 1800. Помітити таку площину дуже легко. Нею є,наприклад, поверхня кулі. Домовимся вважати «прямою» на сфері будь-яке коло великого круга, тобто коло, яке утворюється при перетині сфери площиною, яка проходить через центр кулі. Врезультаті на сфері отримуємо вельми своєрідну геометрію. Отже, на сфері не може існувати ні геометрія Евкліда,ні геометрія Лобачевського. Що стосується трикутників, то сума їхніх кутів завжди більша 180Гр. В деяких випадках сума кутів трикутника може бути рівною 540Гр.

38-39. Поняття величини є складовою змісту багатьох наук: математики, фізики, хімії, біології та ін. Без поняття величини вивчення дійсного світу обмежувалося б лише спостереженнями і залишалось би на описовому рівні. Введення таких величин як довжина, об’єм і температура, встановлення залежності між ними дозволило не тільки значно збагатити знання про світ та інші явища природи, а враховувати їх при розв’язуванні конкретних задач, що пов’язані з практичною діяльністю людини. Умови для введення тієї чи іншої величини визрівають у процесі розвитку даної галузі науки. еличини, які виражають одну і ту ж властивість деякої сукупності об’єктів, називають однорідними, різні властивості – неоднорідними. Так, довжина і площа є неоднорідними величинами. При вимірюванні величин важлива роль вибору одиниць вимірювання. Навіть для вимірювання однієї величини не можна обійтися однією одиницею вимірювання. Наприклад, щоб виміряти довжини зернини пшениці, будинку або залізниці від Києва до Харкова зручніше користуватися міліметром, метром і кілометром відповідно. В різних народів і в різні часи одиниці вимірювання були різними. На Україні здавна урожай рахували «копами» (копа 60 снопів) та «возами» або «хурами» (кількість снопів, яка вміщалася на возі). Рідину – воду, молоко тощо міряли «квартами» (2 пляшки), «гранцями» (4 кварти), «відрами» (10–12 літрів). У ткацькій справі використовувалися одиниці загальнослов’янського походження – «чисниця» (три нитки), «пасмо» (10 чисниць), «моток» (30 пасом). Селянами використовувалися оригінальні одиниці площі землі: «день» (площа, яку можна виорати за день волами), «опруг», «гона», «волока», «лан» та ін.На даний час вона включає: 1) сім основних одиниць: метр (м) – для довжини; кілограм (кг) – для маси; секунда (с) – для часу; моль (моль) – для кількості речовини; кельвін (К) – для термодинамічної температури; кандела (кд) – для сили світла; ампер (А) – для сили електричного струму; 2) дві додаткових одиниці: радіан (рад) – для плоского кута; стерадіан (ср) – для тілесного кута; 3) похідні одиниці, серед яких, наприклад, квадратний метр (м2) – для площі, кубічний метр (м3) – для об’єму. Деякі скалярні величини мають так звану адитивну властивість, яка полягає в тому, що величина допускає необмежене “подріблення”, тобто її можна скласти з частин, що попарно не перетинаються і є теж величинами. Так, час-проміжок має адитивну властивість, а час-дата – ні. Величини, які мають адитивну властивість, називаються адитивно-скалярними величинами. Додатні адитивно-скалярні величини займають особливе місце серед величин. З ними найбільш часто має справу людина в своїй практичній діяльності.

39. Виміряти величину означає встановити її розміри, масу, площу і т. д. Вимірювання різних величин може виконуватись різноманітними інструментами і різними способами. Можна вимірювати відстані між точками, довжини прямолінійних відрізків, довжини дуг кривої, площі фігур, проміжки часу, температуру, густину тіла тощо. Спільним при вимірюванні будь-яких величин є те, що вимірювання завжди є порівняння величини даного роду з певною величиною цього ж роду, взятою за одиницю вимірювання, і вираження результату порівняння числом. Наприклад, довжини відрізків, відстані між точками вимірюються в сантиметрах, кілометрах; площі фігур – у квадратних сантиметрах, квадратних метрах, арах, гектарах; величини кутів виражаються в секундах, градусах, радіанах; тривалість часу – у годинах, хвилинах, днях, роках; температура – в градусах і т. д. Нехай маємо величину Ф певного роду. Візьмемо яку-небудь величину е цього ж роду за одиницю вимірювання. Якщо величину Ф можна розбити на п рівних частин, кожна з яких дорівнює е, то кажуть, що величина Ф кратна величині е, або що величина е вкладається п раз в величині Ф. Це записують так: те (Ф) = п або Ф = пе, де п – натуральне число. Число п називається мірою або числовим значенням величини Ф, виміряної за допомогою одиниці вимірювання е. Воно показує відношення величини Ф до одиниці вимірювання е, тобто на яке число слід помножити одиницю вимірювання е, щоб дістати величину Ф

40. Довжиною відрізка називається додатна величина, визначена для кожного відрізка так, що: 1) рівні відрізки мають рівні довжини; 2) якщо відрізок складається із скінченного числа відрізків, то його довжина дорівнює сумі довжин цих відрізків; 3) існує відрізок, довжина якого дорівнює одиниці. Наведені умови, яким повинна задовольняти довжина відрізка, називаються властивостями або аксіомами довжини. Довжина відрізка задовольняє властивості рефлексивності, симетричності та транзитивності. Два відрізки, які мають спільну міру, називаються сумірними. У іншому разі вони називаються несумірними. Теорема. Довжина відрізка не залежить від вибору спільної міри даного відрізка і даного одиничного відрізка. Т: При довільному виборі одиничного відр. PQ існує відображення L: L->R+, що задовольня 3 акс. вимірювання.

41. Візьмемо на площині прямокутну систему координат хОу і на її осі накладемо десяткові шкали, вибравши одиничний відрізок е. Через штрихи десяткових шкал проведено прямі, паралельні координатним осям х і у. При цьому вся площина розіб’ється на рівні квадрати, сторона яких дорівнює одиничному відрізку е. Площа кожного такого квадрата дорівнює одиниці. Фігура F називається квадровною, якщо вона повністю покривається ступінчастою фігурою, утвореною з квадратів сітки, і якщо існує хоч би один як завгодно малий квадрат з покриття, який повністю складається з внутрішніх точок фігури F. Якщо ці умови не виконуються для якоїсь фігури, то площа такої фігури дорівнює нулю. Т: Кожна многокутна фігура має певну площу. Т: Існує причому єдина ф-я з властивостями 1-4 визначена на множ. многокутної фігури. Т: фігура має визначену площу тоді і тільки тоді коли площа її основи = 0. Т: Будь – яка фігура яка обмежена скінченою кількість криволінійними відрізками має визначену площу.

42. Геометричним еквівалентом поняття рівно великості( це плоскі фігури з однаковою площею або просторові фігури з однаковим об’ємом), який дає змогу перетворювати многокутники так, щоб встановити їх рівновеликість, є поняття рівноскладеності многокутників. Два многокутники називаються рівноскладеними, якщо їх можна розкласти на одне й те саме число попарно рівних многокутників. З означення маємо такі властивості рівноскладеності многокутників. 1. Кожний многокутник рівноскладений сам собі. 2. Якщо многокутник Р рівноскладений з многокутником Р1 то й многокутник Р1 рівноскладений з многокутником Р. 3. Два многокутники, рівноскладені з одним і тим самим третім многокутником, рівноскладені між собою. Твердження про рівновеликість і рівноскладеність многокутників пов’язані між собою. Т: Бойяї - Гервіна. Будь-які два многокутники рівновеликі то вони рівноскладені.

43. Лема: Відношення рівно складеної є відношення еквівалентне. Лема: Кожен трикутник рівно складений з деяким прямокутником. Лема: Два прямокутники які мають рівні площі є рівно складені. Лема: Кожен многокутник рівно складений з деяким прямокутником.

Дата добавления: 2016-01-04; просмотров: 15; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12

Мы поможем в написании ваших работ!